Scroll 正在构建 zkRollup 的以太坊通用扩容解决方案,使用了非常先进的算术化电路和证明系统,并且通过硬件加速构建快速的验证器,证明递归。
撰文:Ye Zhang
编译:F.F
在最新的 ZKP Mooc 课程中,Scroll 的联合创始人张烨发表了关于 zkEVM 设计,优化和应用的演讲。Scroll 在构建以太坊等效的 ZK-Rollup,在字节码级别的兼容,直接支持所有现有的工具。
以下是视频的听录文字版本。
演讲分成四个部分,第一部分张烨介绍了开发背景以及我们为什么首先需要 zkEVM 以及为什么它在最近两年间变得如此受欢迎,第二部分通过一个完整的流程,讲解如何从头开始构建 zkEVM 包括算术化和证明系统,第三部分通过一些有趣的研究问题来谈论了 Scroll 在构建 zkEVM 时遇到的问题,最后介绍了一些其他使用 zkEVM 的应用。


背景和动机

传统的 Layer 1 区块链会有一些节点通过 P2P 网络共同维护。他们在收到用户的交易时,会在 EVM 的虚拟机内执行,读取调用合约和存储,并依照交易更新全局的状态树。
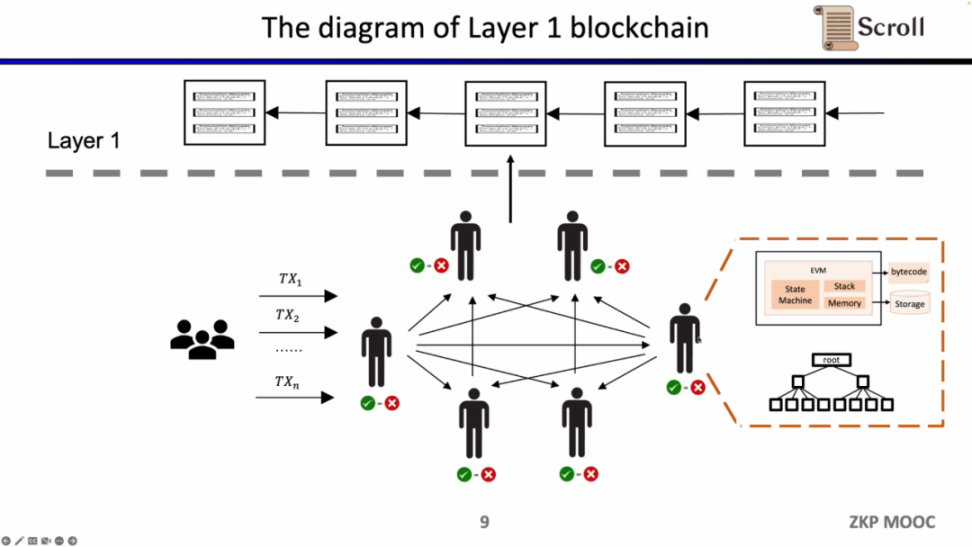
这样的架构的优势在于去中心化和安全性,缺陷就是在 L1 上的交易手续费昂贵,并且交易确认缓慢。
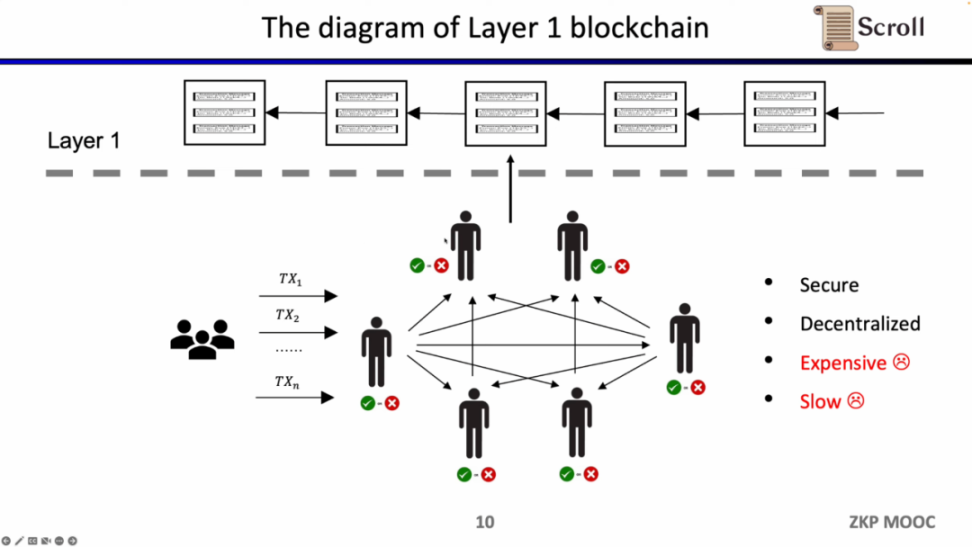
ZK-Rollup 的架构中,L2 网络只需将数据和验证数据正确性的证明上传至 L1,其中证明通过零知识证明电路计算而来。
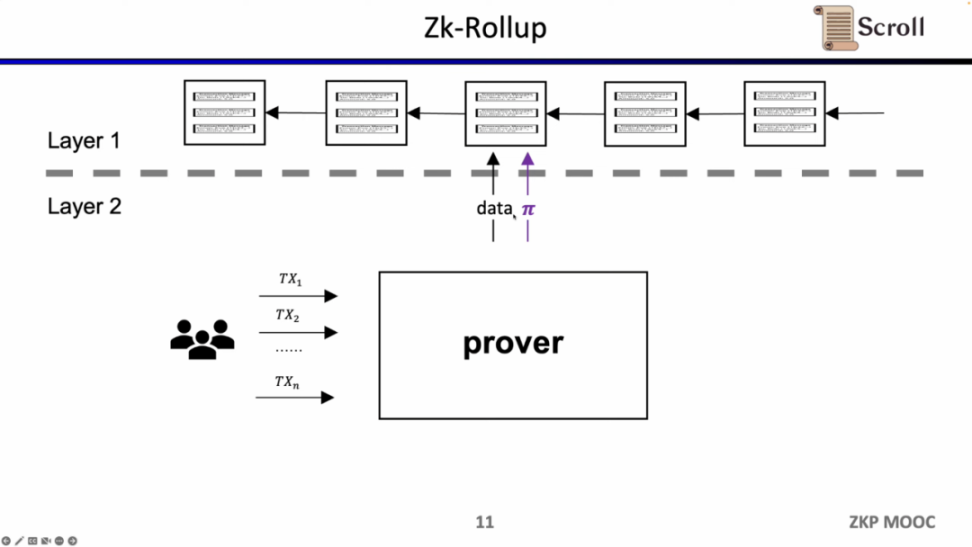
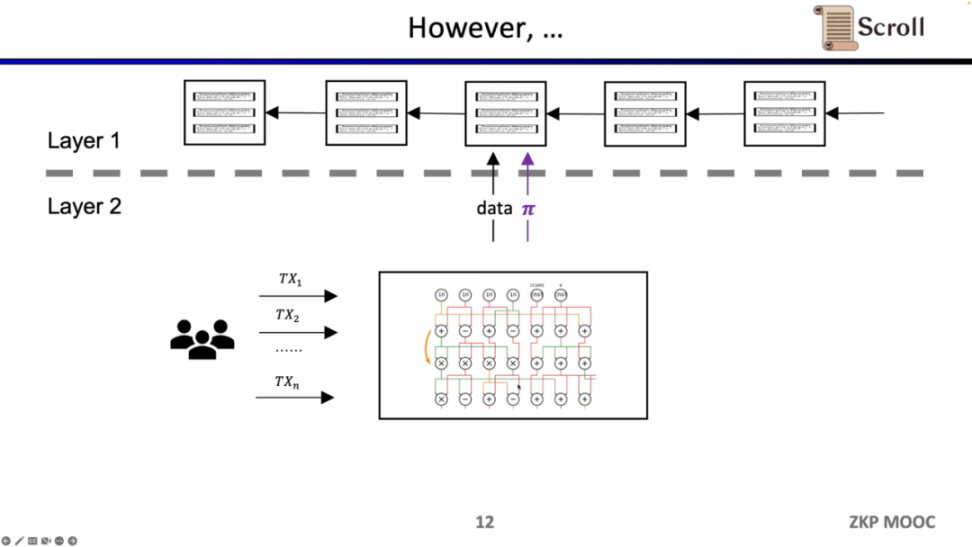
在早期的 ZK-Rollup 中,电路是针对特定应用而设计,用户需要将交易发送给不同的证明者,然后不同应用的 ZK-Rollup 再将自己的数据和证明提交至 L1。这样带来的问题是,丧失了原先 L1 合约的可组合性。
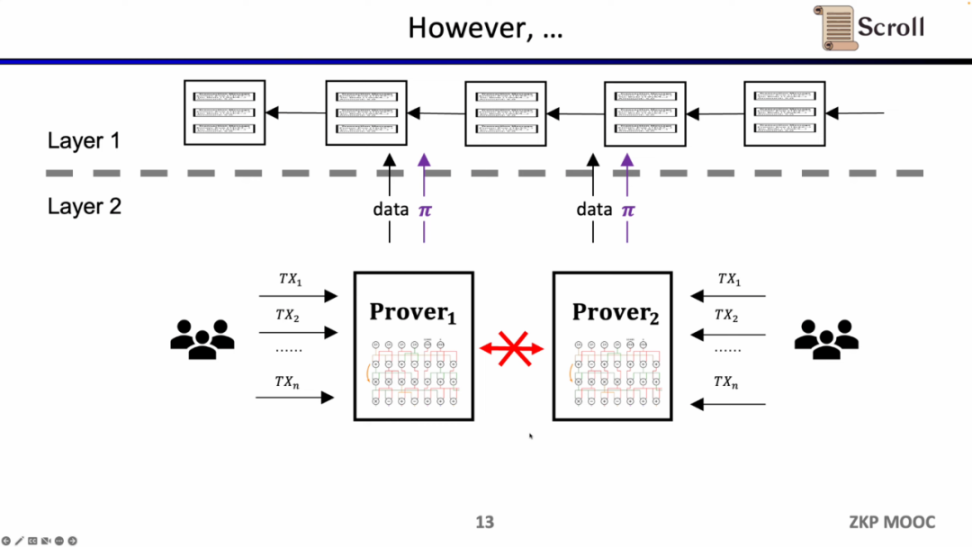
Scroll 所要做的是原生的 zkEVM 方案,是一种通用型的 ZK-Rollup。这样不仅对用户而言更友好,对于开发者而言也可以获得在 L1 上的开发体验。当然这背后的开发难度非常之大,并且现在的证明生成的代价也非常高。
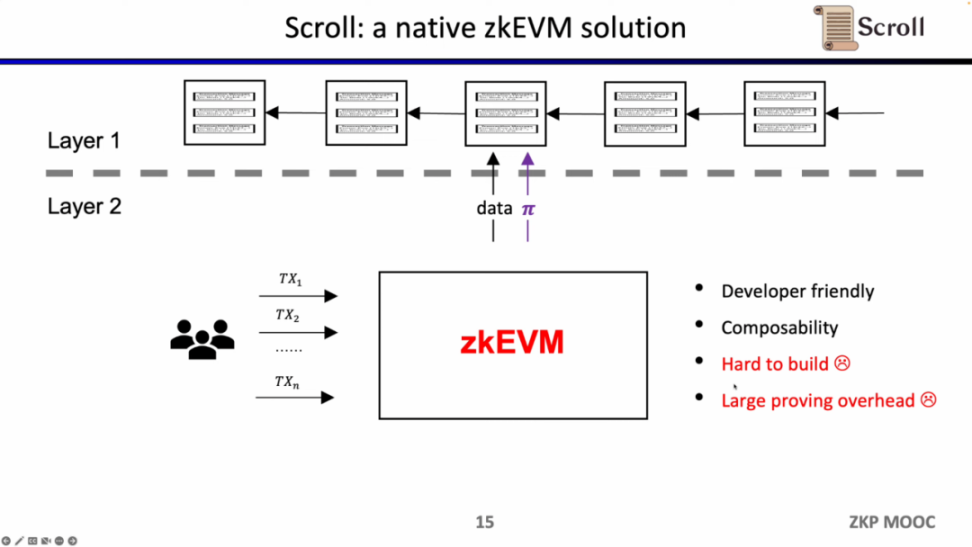
幸运的是,零知识证明的效率在过去两年里已经大幅提高了,这也是为什么在最近两年 zkEVM 变得如此受欢迎。至少有四个原因让它变得可行,第一是多项式承诺的出现,在原先 Groth16 证明系统下,约束的规模非常之庞大,而多项式承诺可以支持更高阶的约束,缩小证明规模;第二是查找表和自定义门的出现,可以支持更灵活的设计,使证明更加高效;第三是硬件加速方面的突破,通过 GPU,FPGA 和 ASIC 可以将证明时间缩短 1-2 个数量级,第四是在递归证明下,可以将多个证明压缩成一个证明,使得证明变得更小更易于验证。所以结合这四个因素,零知识证明的生成效率要比两年前高出三个数量级,这也是 Scoll 的起源。
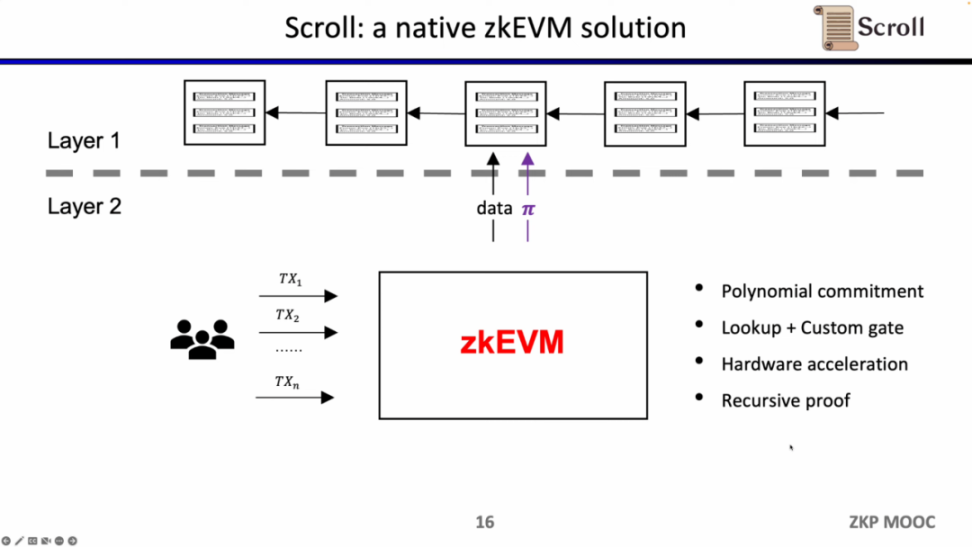
根据 Justin Drake 的定义,zkEVM 可以分为三类,第一类是语言级别的兼容,主要原因是 EVM 不是为 ZK 而设计,有很多对 ZK 不友好的操作码,因此会造成大量的额外开销。因此像 Starkware 和 zkSync 选择在语言层面将 Solidity 或者 Yul 编译到 ZK 友好的编译器中。
第二类是 Scroll 在做的字节码层面的兼容,是直接证明 EVM 的字节码处理正确与否,直接继承了以太坊的执行环境。在这里可做的一些取舍是,使用和 EVM 不一样的状态根,例如使用 ZK 友好的数据结构。Hermez 和 Consensys 也在做类似的事情。
第三类是共识层面的兼容,这里的取舍在于不仅需要保持 EVM 不变,还包括储存结构等实现以太坊完全兼容,代价是需要更长的证明时间。而 Scroll 正在和以太坊基金会的 PSE 团队合作构建,来实现以太坊的 ZK 化

从 0 到 1 构建 zkEVM

第二部分,张烨向大家展示了如何从零开始建立 ZKVM。
完整流程
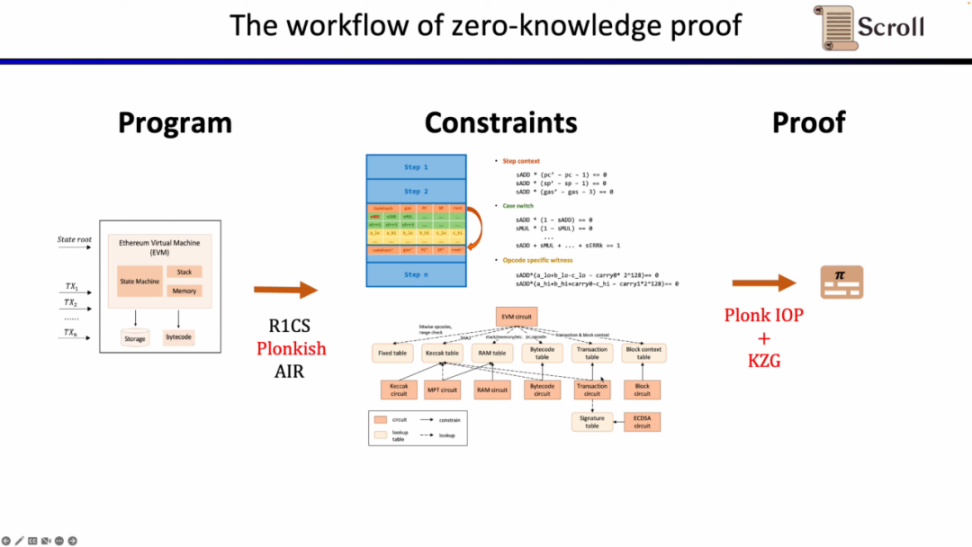
首先,在 ZKP 的前端部分,你需要通过数学的算术化来表示你的计算,最常用的就是线性的 R1CS,以及 Plonkish 和 AIR。通过算术化得到约束后,在 ZKP 的后端你需要运行证明算法,来证明计算正确性,这里列举了最常用的多项式交互式谕示证明 (Polynomial IOP) 和多项式承诺方案 (PCS)。
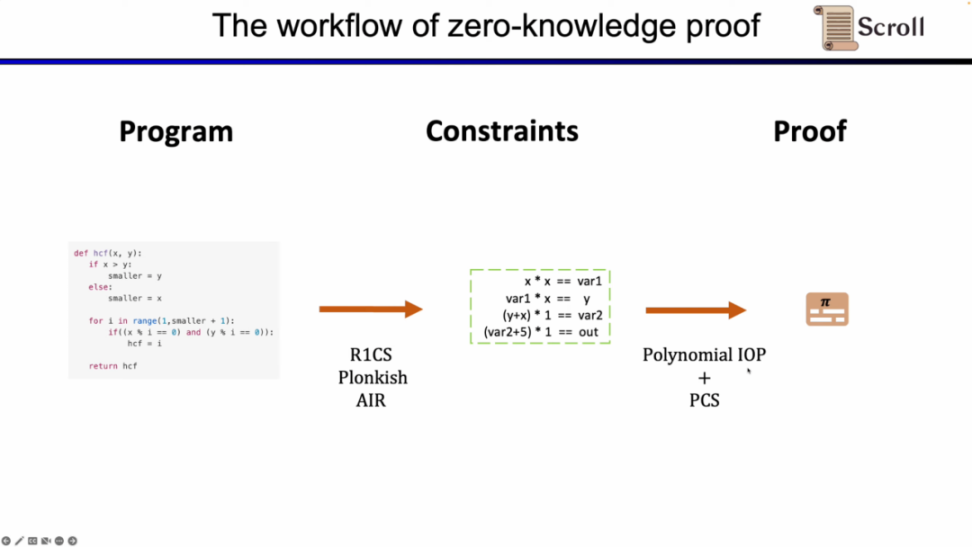
在这里我们需要证明 zkEVM,Scroll 使用的是 Plonkish,Plonk IOP,以及 KZG 的组合。
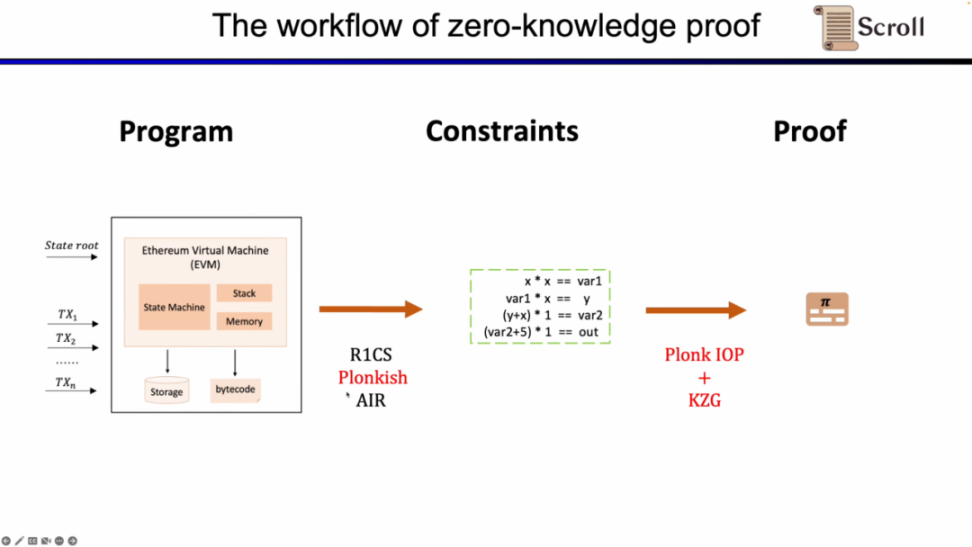
为了理解我们为什么使用这三者的方案。我们首先从最简单的 R1CS 开始,R1CS 中的约束,是线性组合乘以线性组合等于线性结合。你可以加上任何变量的线性组合而没有额外的开销,但是在每个约束中阶数最大是 2。因此对于阶数较高的运算,需要的约束就越多。

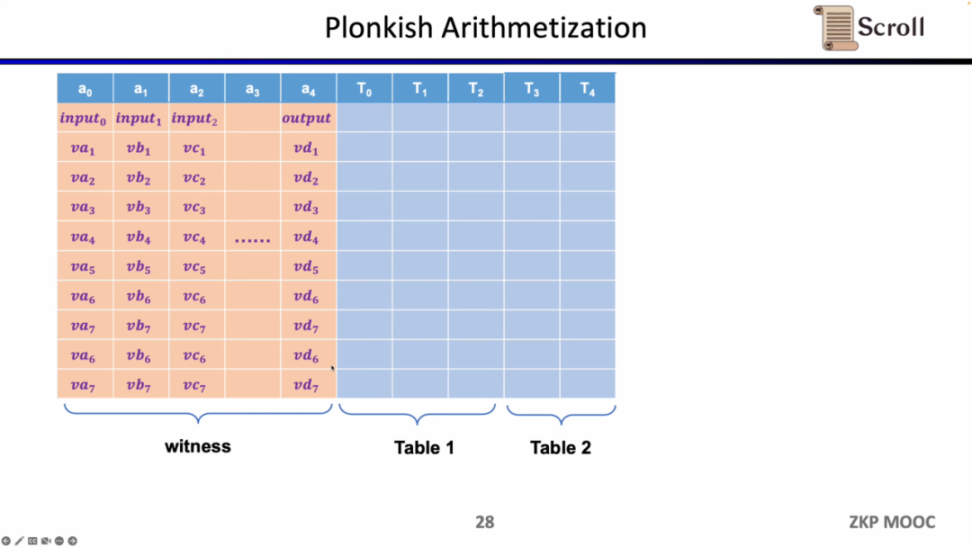
而在 Plonkish 中,你需要将所有的变量填入表格,包括输入,输出以及中间变量的见证。在此之上,你可以定义不同的约束。在 Plonkish 中有三种类型的约束可以使用。
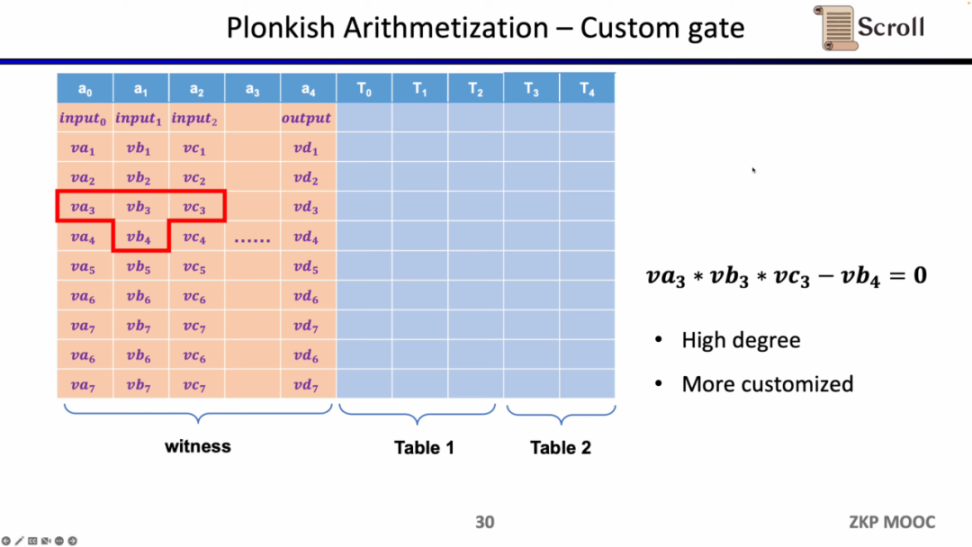
第一种约束是自定义门(Custom Gate),你可以定义不同单元格之间的多项式约束关系,例如 va3 * vb3 * vc3 - vb4 =0。相比 R1CS 来说,阶数可以更高,因为你可以定义任何一个变量的约束,并且可以定义一些非常不一样的约束。
第二种约束是 Permuation,即等价性校验 (equality checks)。可以用来检查不同单元格的等价性,常用于关联电路中的不同门,比如证明上一个门的输出等于下一个门的输入。

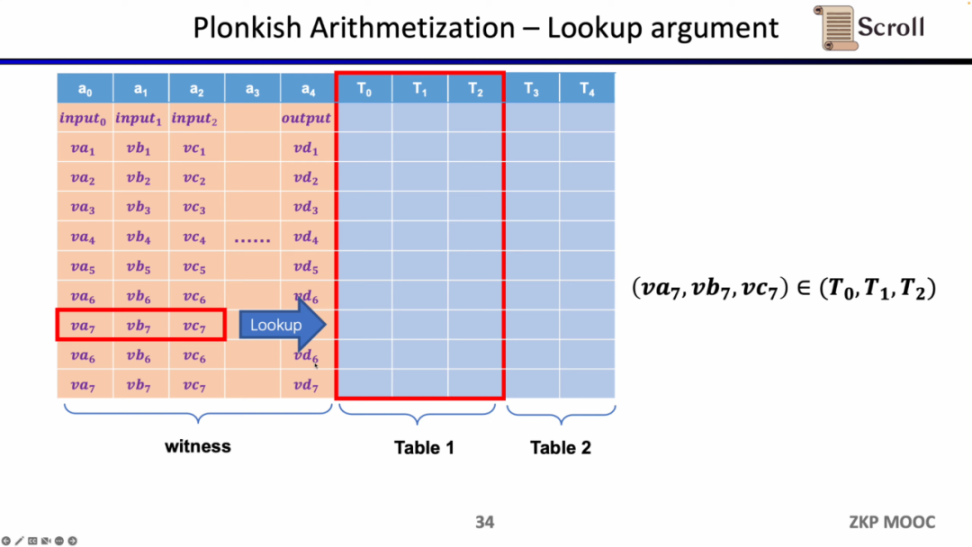
最后一种约束是查找表 (Lookup Table)。我们可以将查找表理解成变量之间存在一个关系,该关系可以表示成一个表。例如我们想要证明 vc7 在 0-15 范围内,在 R1CS 中你首先需要把这个数值分解为 4 位二进制,然后证明每位在 0-1 的范围内,这将需要四个约束。而在 Plonkish 中,你可以将所有可能的范围列在同一列,只需要证明 vc7 属于该列即可,这对范围证明非常高效,在 zkEVM 中,查找表对于证明内存读写非常有用。
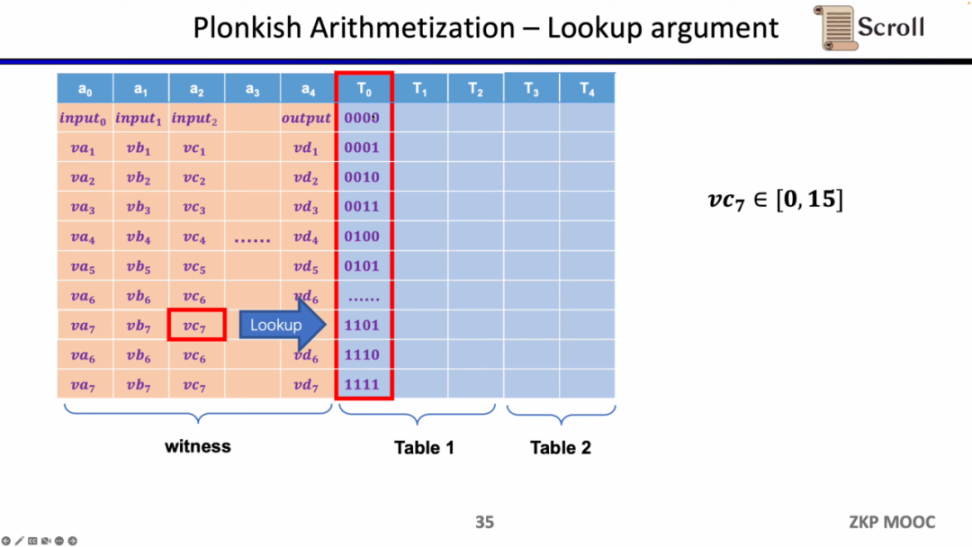
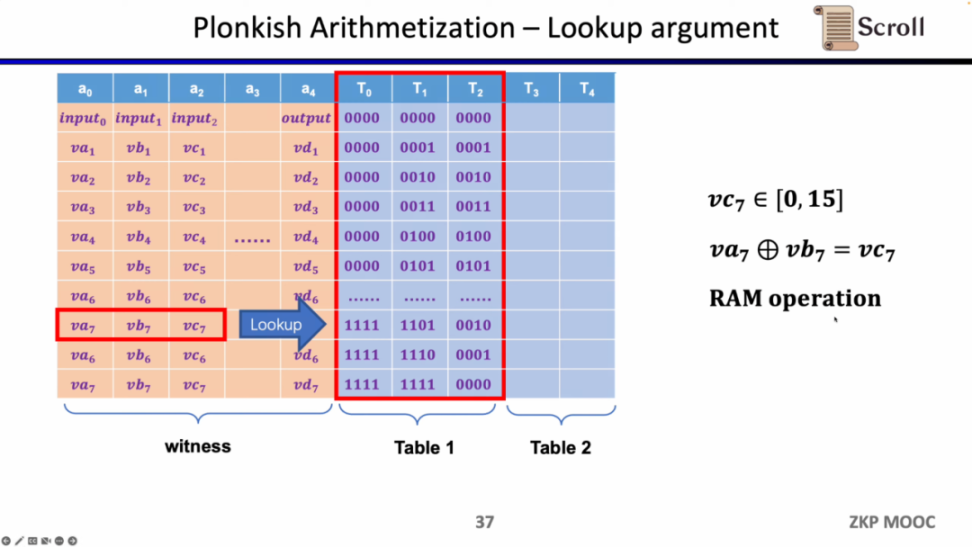
小结一下,Plonkish 同时支持自定义门,等价性校验和查找表,可以非常灵活的满足不同的电路需要。简单对比下 STARK,STARK 中每一行是一个约束,约束需要表示行与行之间的状态转换,但 Plonkish 中的自定义约束灵活性显然更高。

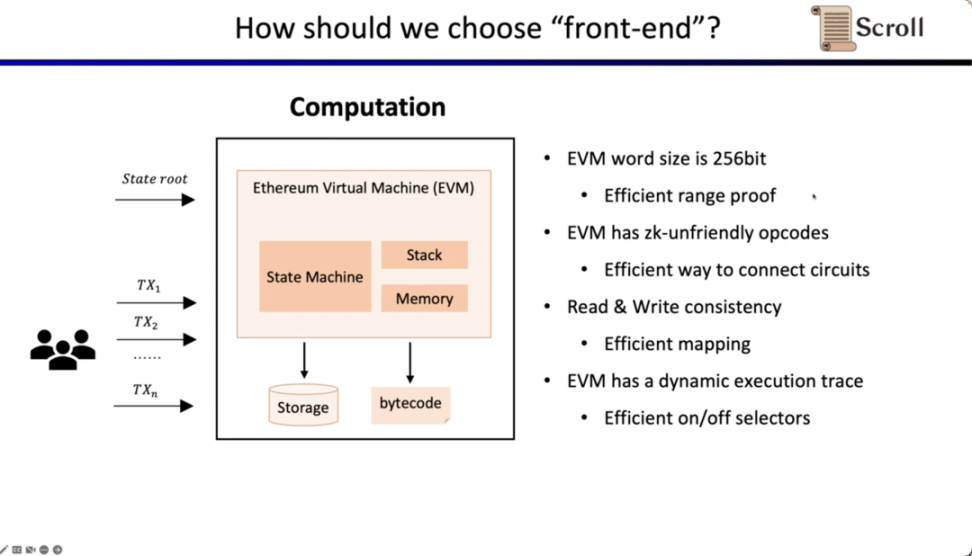
现在的问题是在 zkEVM 中,我们如何选择前端。对于 zkEVM 主要有四个挑战。第一个挑战是 EVM 的字段是 256 位,这意味着需要高效得对变量进行范围约束;第二个挑战是 EVM 有很多 ZK 不友好的操作码,因此需要非常大规模的约束来证明这些操作码,例如 Keccak-256;第三个挑战是内存读写问题,你需要一些有效的映射来证明你所读取的和之前所写入的是一致的;第四个挑战是 EVM 的执行踪迹是动态变化的,因此我们需要自定义门来适配不同的执行踪迹。出于上述的考虑,我们选择了 Plonkish。
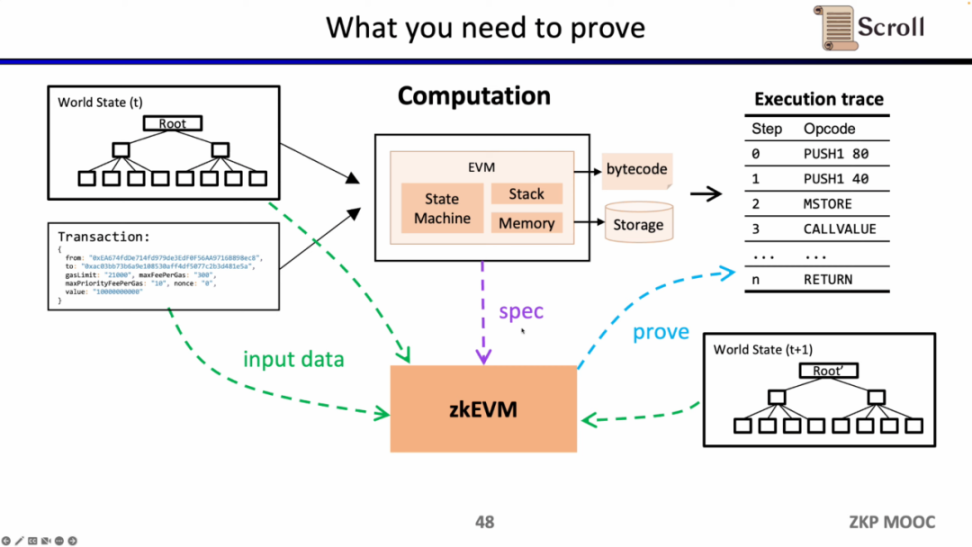
接下来,我们看 zkEVM 的完整流程,基于初始的全局状态树,一笔新的交易进来后,EVM 会读取存储和调用的合约的字节码,根据交易生成相应的执行踪迹例如 PUSH, PUSH, STORE, CALLVALUE,然后逐步执行更新全局状态,得到交易后的全局状态树。而 zkEVM 是将初始的全局状态树,交易本身,以及交易后的全局状态树作为输入,根据 EVM 的规范,来证明执行踪迹的执行正确性。
深入 EVM 电路细节,每一步执行踪迹都有对应的电路约束。具体来说,每一步的电路约束包含 Step Context,Case Switch,Opcode Specific Witness。Step Context 包含执行踪迹对应的 codehash,剩余 gas 和计数器;Case Switch 包含所有的操作码,所有的错误情况,以及该步的相应操作;Opcode Specific Witness 包含了操作码所需的额外见证,例如运算数等。
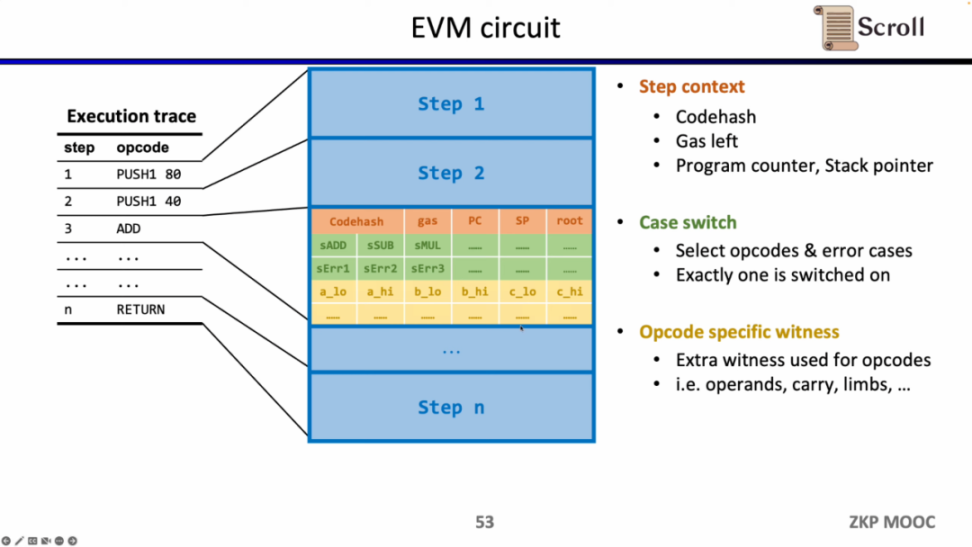
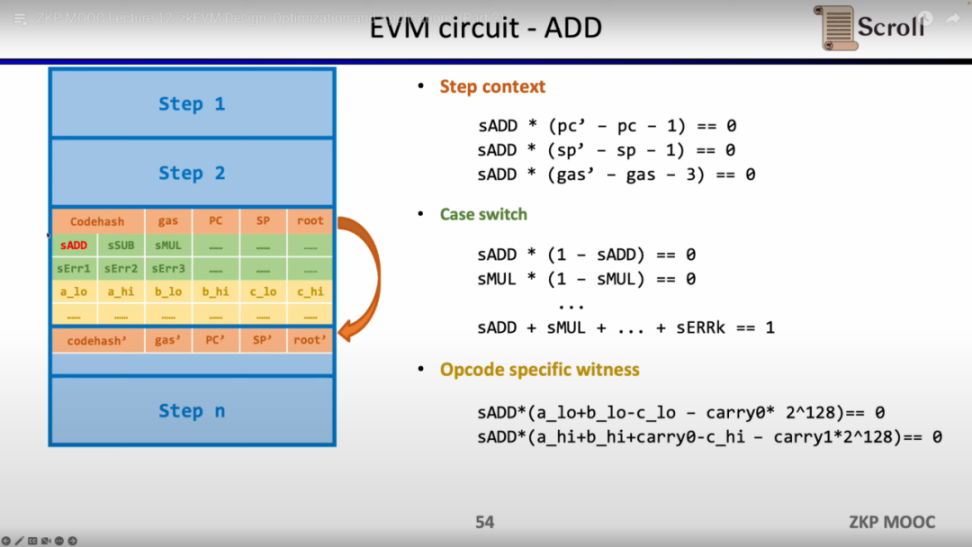
以简单的加法为例,需要确保加法的操作码的控制变量 sADD 设置为 1,其他操作码控制变量均为零。在 Step Context 中,通过设置 gas' - gas - 3 = 0 来约束消耗的 gas 等于 3, 同理约束计数器,栈指针在该步后累加 1;在 Case Switch 中,通过操作码控制变量和为 1 来约束该步为加法操作;在 Opcode Specific Witness 中,对运算数的实际加法进行约束。
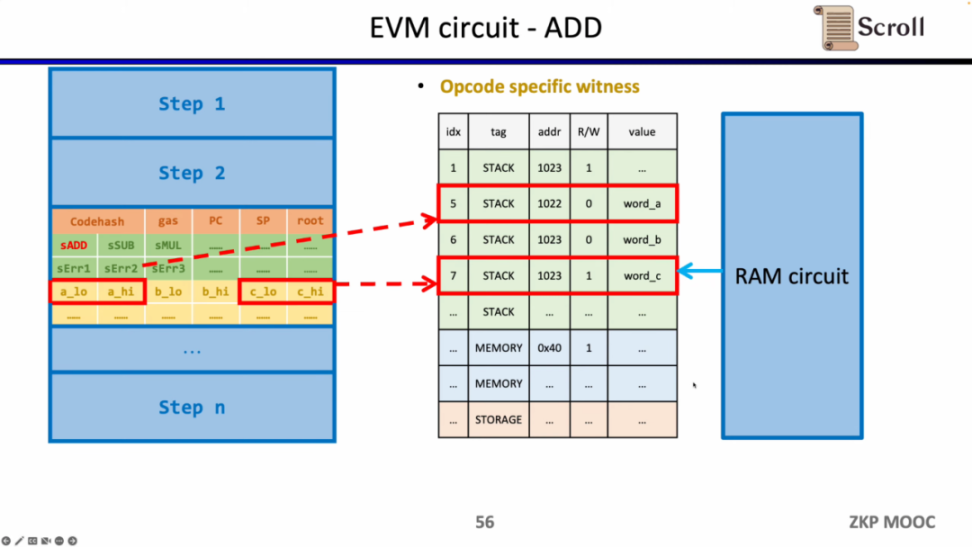
此外还需要额外的电路约束,来保证运算数从内存读取的正确性。这里我们首先需要构建一个查找表来证明运算数属于内存。并通过内存电路 (RAM Circuit) 来验证内存表的正确性。
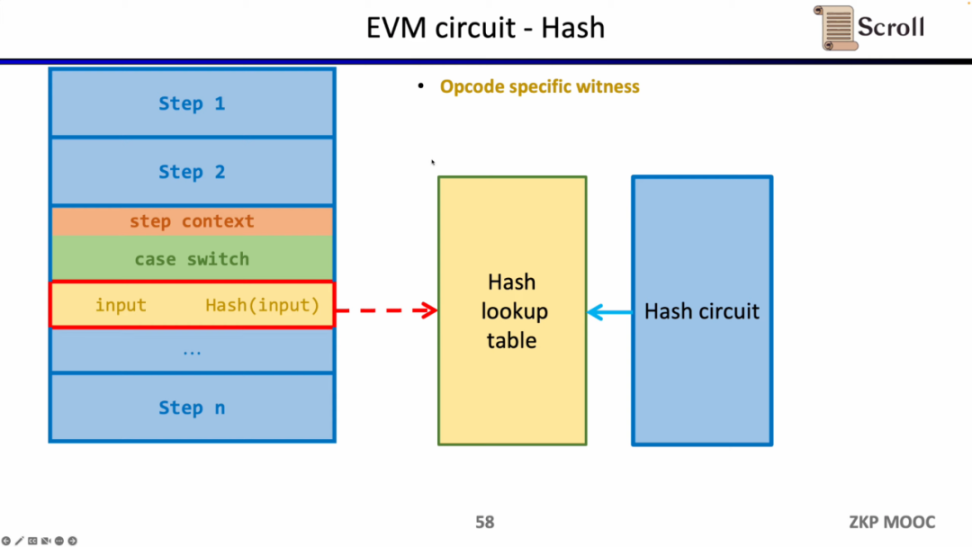
同样的方法可以适用于 zk 不友好的哈希函数,构建哈希函数的查找表,将执行踪迹中的哈希输入和输出映射到查找表,利用额外的哈希电路 (Hash Circuit) 来验证哈希查找表的正确性。
现在我们来看 zkEVM 的电路架构,核心的 EVM 电路用于约束执行踪迹每一步的正确性,在一些 EVM 电路约束难度较大的地方,我们通过查找表来映射,包括 Fixed Table, Keccak Table, RAM Table, Bytecode, Transaction, Block Context,然后利用单独的电路来约束这些查找表,例如 Keccak 电路用于约束 Keccak 表。
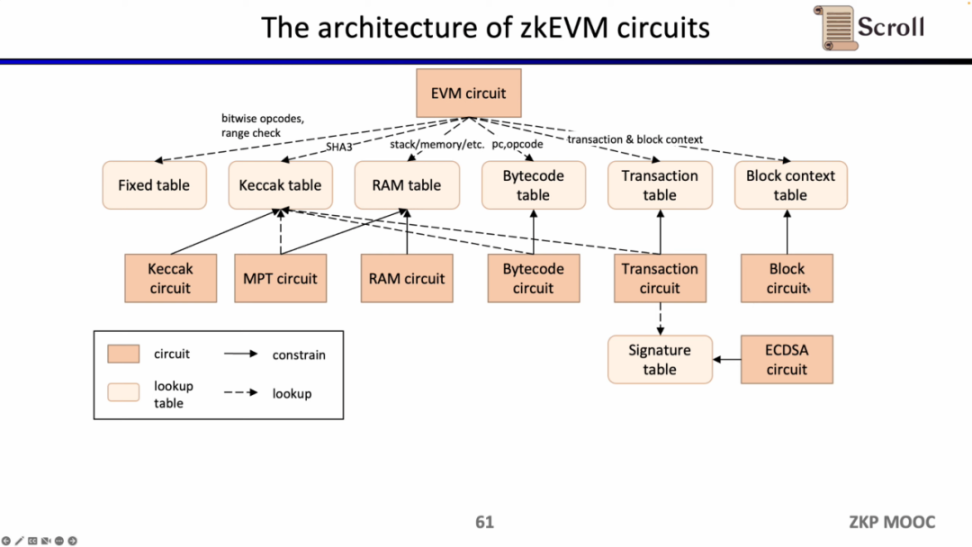
小结一下,zkEVM 的完整工作流如下图所示。
证明系统
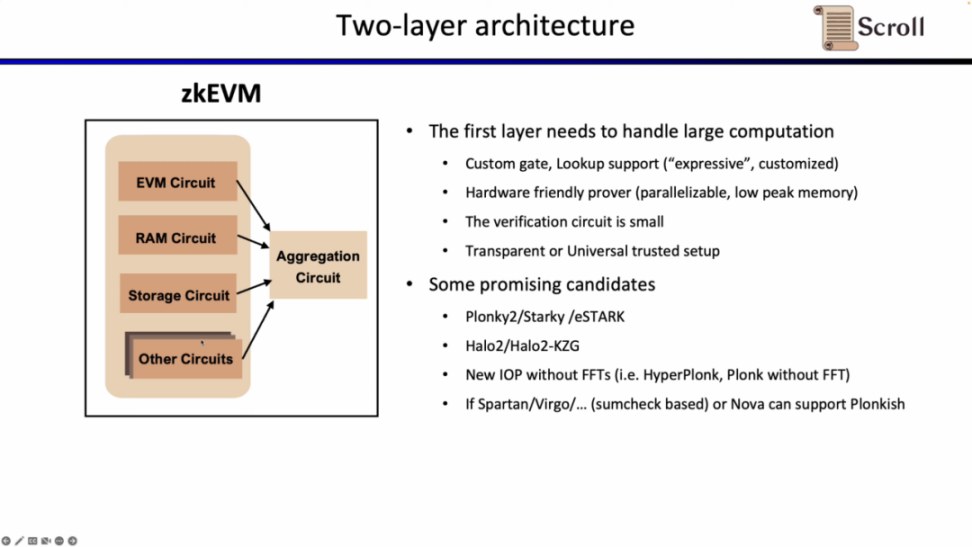
因为在 L1 上直接验证上述的 EVM 电路,内存电路,存储电路等,开销巨大,Scroll 的证明系统采用了两层架构。
第一层负责直接证明 EVM 本身,需要大量的计算来生成证明。因此第一层证明系统要求支持自定义门和查找表,对硬件加速友好,在低峰值内存下并行生成计算,且验证电路规模小,可以快速验证。有前景的可选方案包括 Plonky2,Starky,eSTARK,它们前端基本上都使用 Plonk,但后端可能使用了 FRI,并且都满足上述的四个特性。另一类可选的方案包括 Zcash 所开发的 Halo2,以及 KZG 版本的 Halo2。
还有一些新的证明系统也有很有前景,例如最近移除了 FFT 的 HyperPlonk,而 NOVA 证明系统可以做到更小的递归证明。但它们在研究中只支持 R1CS,如果他们未来可以支持 Plonkish 并且应用于实践,将非常实用高效。
第二层证明系统用于证明第一层证明的正确性,需要可以在 EVM 中高效进行验证,理想情况下,最好也是硬件加速友好并且支持 transparent 或者 universal setup。有前景的可选方案包括 Groth16 和列数较少的 Plonkish 证明系统。Groth16 仍然是目前研究中证明效率极高的代表,而 Plonkish 证明系统在列数较少的情况下,也可以达到较高的证明效率。
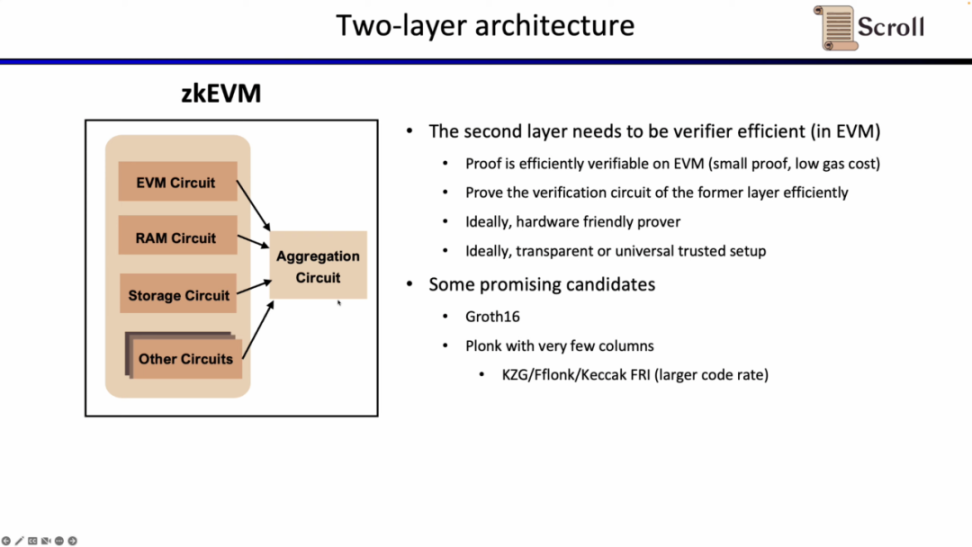
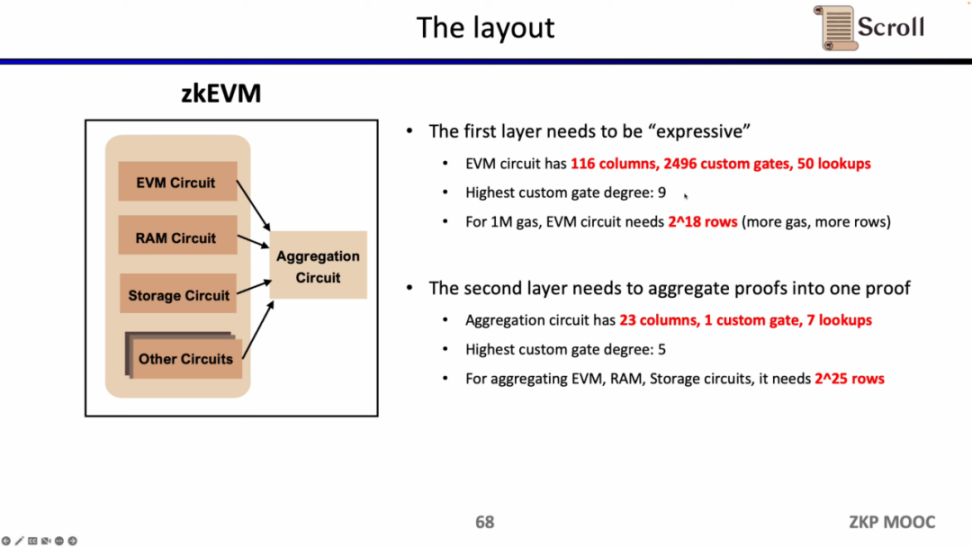
在 Scroll,我们在两层证明系统中我们都采用了 Halo2-KZG 证明系统。因为 Halo2-KZG 可以支持自定义门和查找表,在 GPU 硬件加速下性能良好,且验证电路规模小,可以快速验证。区别在于我们在第一层证明系统中我们使用了 Poseidon 哈希,进一步提高证明效率,而第二层证明系统因为直接在以太坊上验证,仍然使用了 Keccak 哈希。Scroll 也在探索多层证明系统的可能性,来进一步聚合第二层证明系统生成的聚合证明。
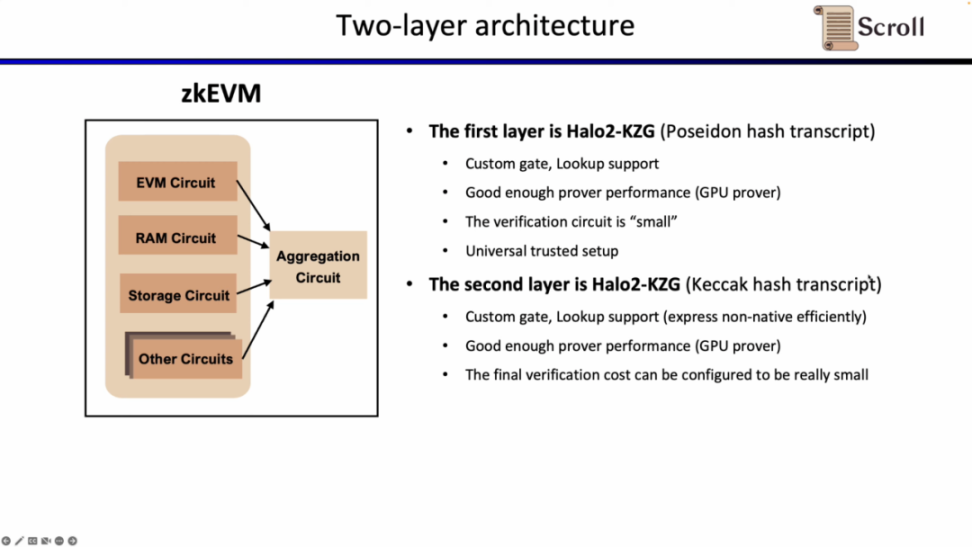
当前实现下,Scroll 的第一层证明系统 EVM 电路有 116 列,2496 个自定义门,50 个查找表,最高阶数为 9,1M Gas 下需要 2^18 行;而第二层证明系统的聚合电路仅有 23 列,1 个自定义门,7 个查找表,最高阶数为 5 ,为了聚合 EVM 电路,内存电路,存储电路,需要 2^25 行。
Scroll 在 GPU 硬件加速方面也做了非常多的研究和优化工作,对于 EVM 电路,优化后的 GPU 证明者仅需 30s,相较 CPU 证明者提升了 9 倍的效率;而对于聚合电路,优化后的 GPU 证明者仅需 149s,相较 CPU 提升了 15 倍的效率。在当前的优化条件下, 1M Gas 第一层证明系统大约需要 2 分钟,第二层证明系统大约需要 3 分钟。

有趣的研究问题

第三部分,张烨谈论了一些 Scroll 在构建 zkEVM 过程中有趣的研究问题,从前端的算术化电路到证明者的实现。
电路
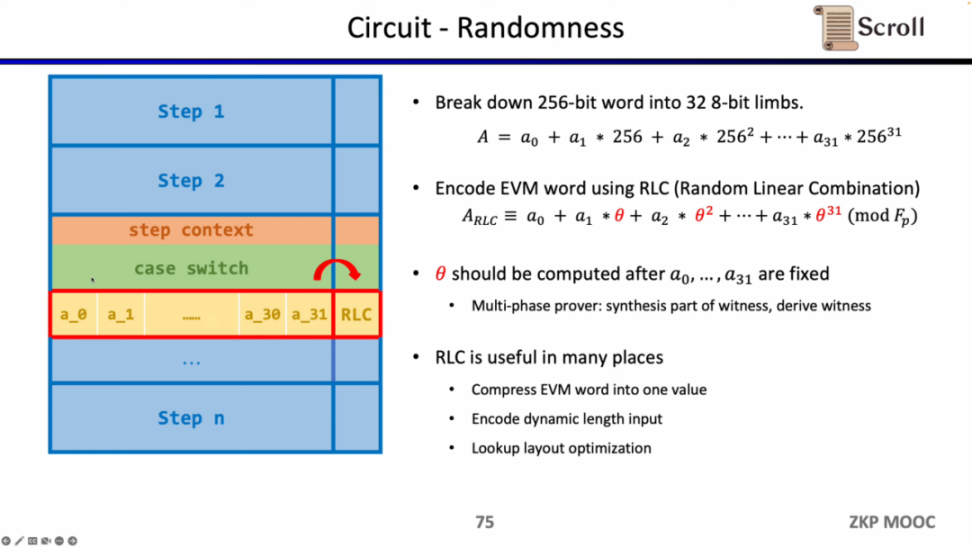
首先是电路中的随机性,因为 EVM 字段是 256 位,我们需要将其拆分成 32 个 8 位的字段,从而更高效得进行范围证明。随后我们使用随机线性组合 (Random Linear Combination, RLC) 的方法,利用随机数将 32 个字段编码成 1 个,只需要验证该字段就可以验证原始的 256 位字段。但是问题在于随机数的生成需要在拆分字段之后,才能确保不被篡改。因此 Scroll 和 PSE 团队提出了多阶段证明者的方案,来确保在字段拆分之后,再利用随机数生成 RLC,该方案被封装在了 Challenge API 中。RLC 在 zkEVM 中有许多应用场景,不仅可以压缩 EVM 字段成一个字段,也可以加密不定长的输入,或是优化查找表的布局,但仍然有许多开放性的问题需要解决。
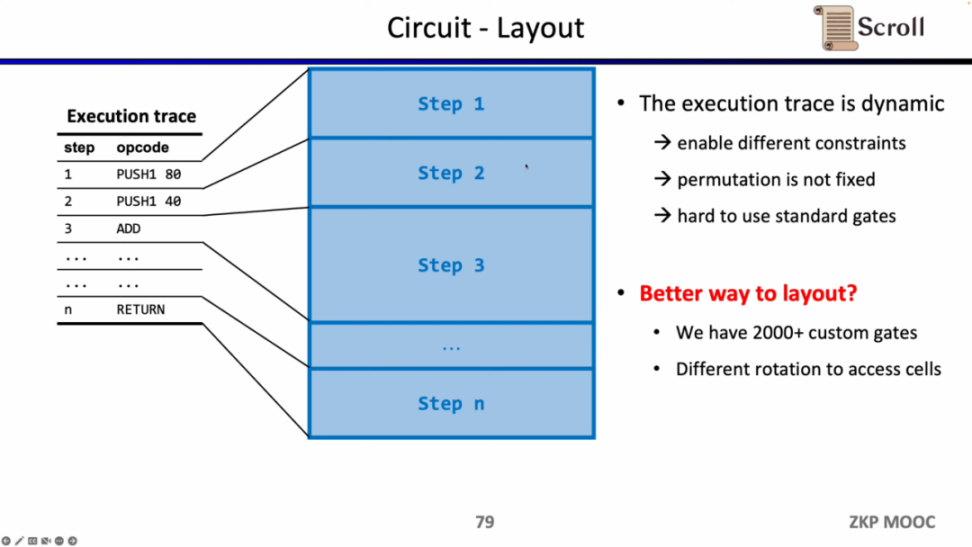
电路方面第二个有趣的研究问题是电路布局。Scroll 前端之所以采用 Plonkish,是因为 EVM 的执行踪迹是动态变化的,需要能支持不同的约束,变化的等价性检验,而 R1CS 的标准化门需要更大的电路规模来实现。但 Scroll 目前使用了 2000 多个自定义门来满足动态变化的执行踪迹,也在探索如何进一步优化电路布局,包括将 Opcode 拆分成 Micro Opcode,或是复用相同表格内的单元格。
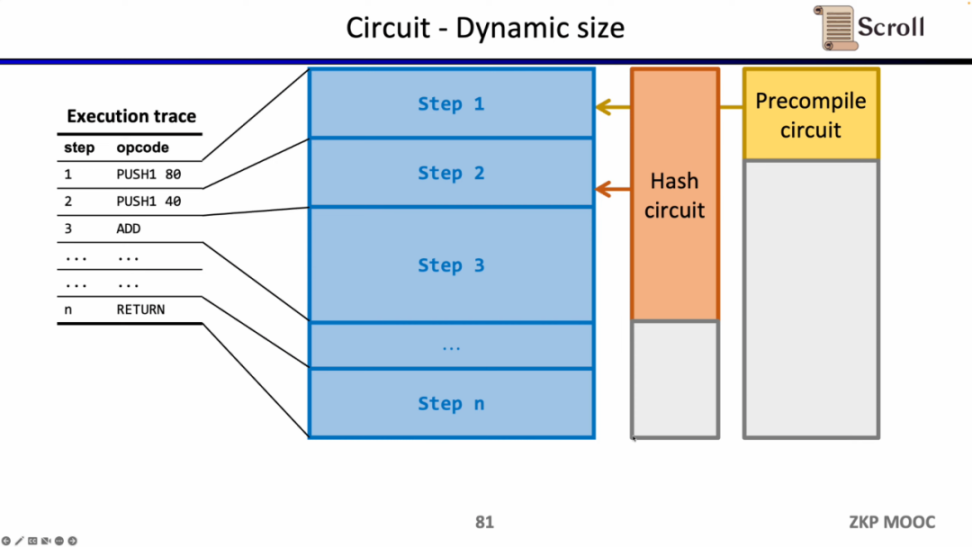
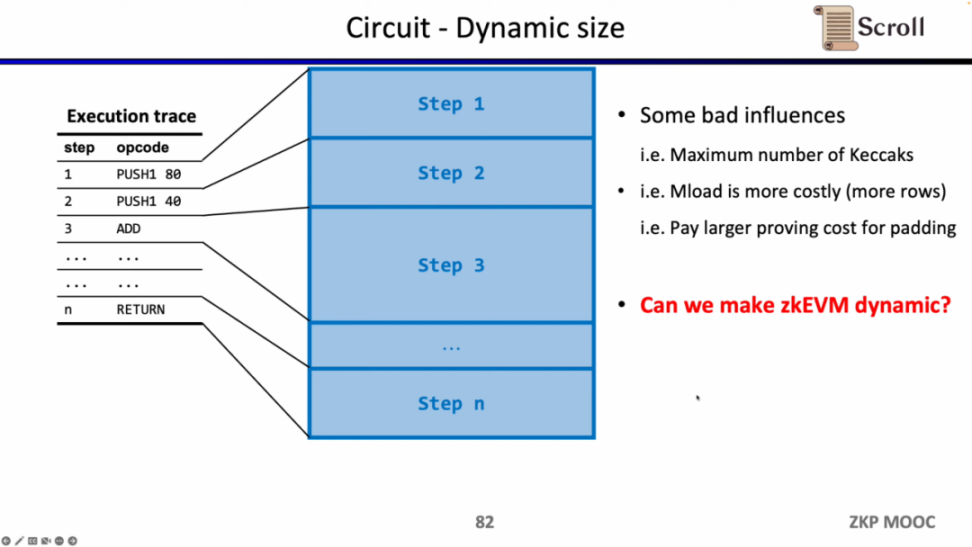
电路方面第三个有趣的研究问题是动态规模。因为不同的操作码的电路规模不同,但为了满足动态变化的执行踪迹,每一步的操作码都需要满足最大的电路规模,例如 Keccak 哈希,因此我们实际上付出了额外的开销。假设我们可以使 zkEVM 动态适应动态变化的执行踪迹,这将节省不必要的开销。
证明者
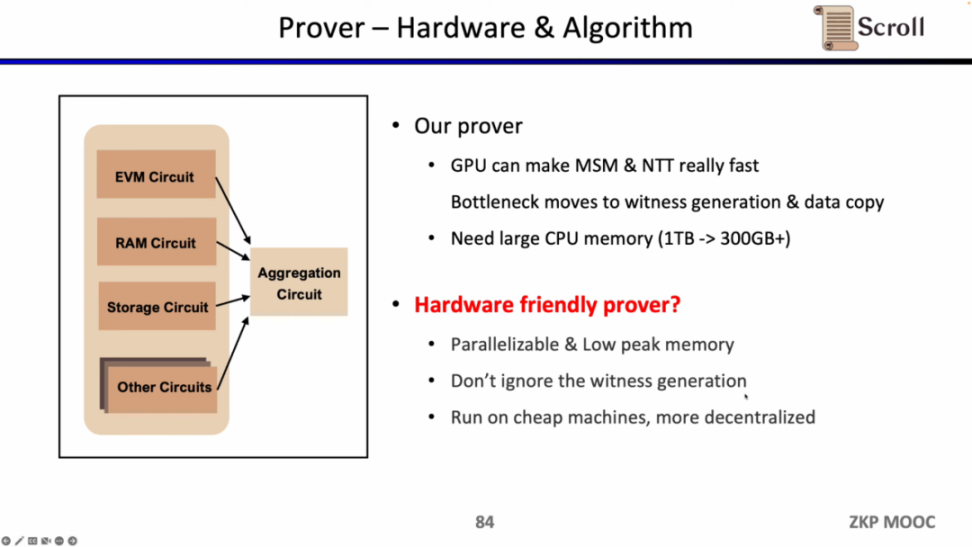
在证明者方面,Scroll 在 GPU 加速上已经对 MSM 和 NTT 进行了大量的优化,但现在的瓶颈转移到了见证生成和复制数据这块。因为假设 MSM 和 NTT 占据了 80% 的证明时间,即使硬件加速可以将这部分效率提升若干个数量级,但原先见证生成和复制数据 20% 的证明时间将变成新的瓶颈所在。证明者的另一个问题是需要大量的内存,因此也需要探索更便宜更去中心化的硬件方案。
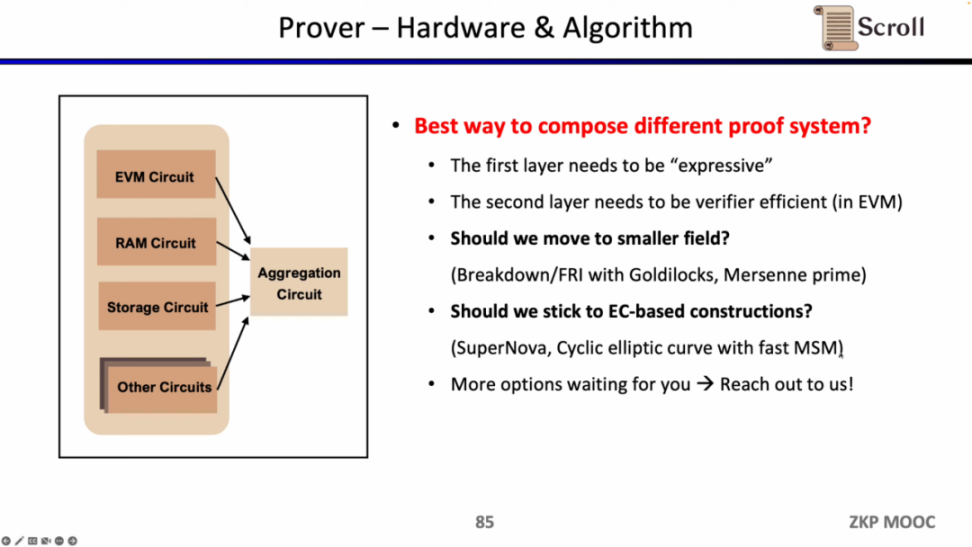
同时 Scroll 也在探索硬件加速和证明算法方面,来提升证明者的效率。目前主要有两个大方向,或是切换至更小的域,例如使用 64 位的 Goldilocks 域,32 位的梅森数(Mersenne Prime)等,或是坚持基于椭圆曲线(EC)的新证明系统,例如 SuperNova。当然也有其他的一些别的可能路径,欢迎有想法的朋友直接联系 Scroll。
安全性
在构建 zkEVM 时,安全性是至关重要的。PSE 和 Scroll 共同构建的 zkEVM 有大约 3 万 4 千行代码,从软件工程角度,这些复杂的代码库在很长一段时间内是不可能没有漏洞的。Scroll 目前在通过大量的审计,包括业内最顶尖的审计公司,来审核 zkEVM 的代码库。



第四部分探讨了其他一些使用了 zkEVM 的应用。
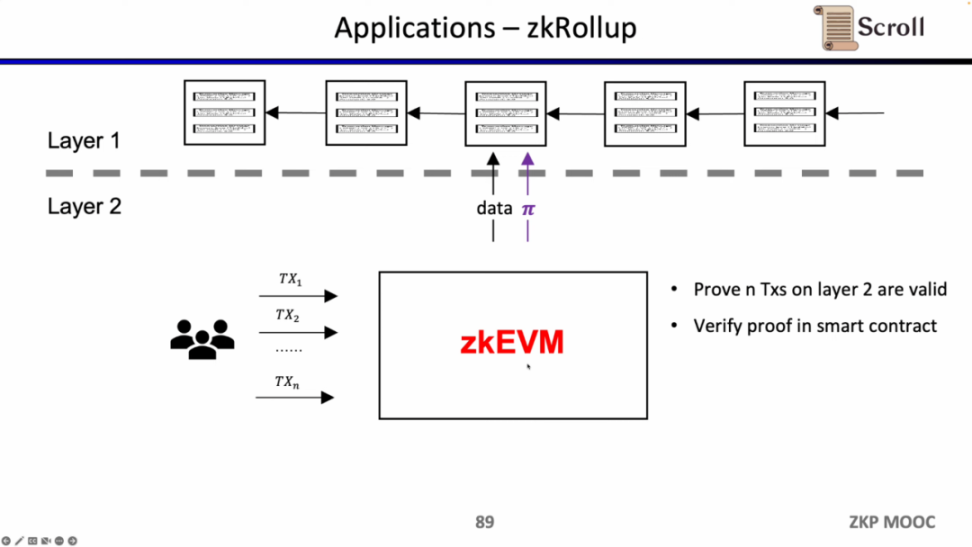
在 zkRollup 的架构中,我们通过在 L1 的智能合约,来验证在 L2 上的 n 笔交易是有效的。
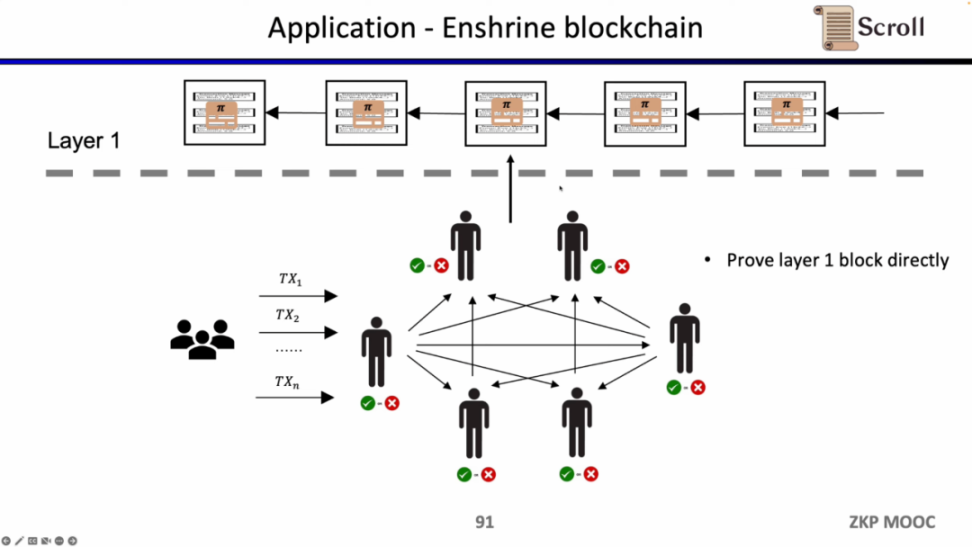
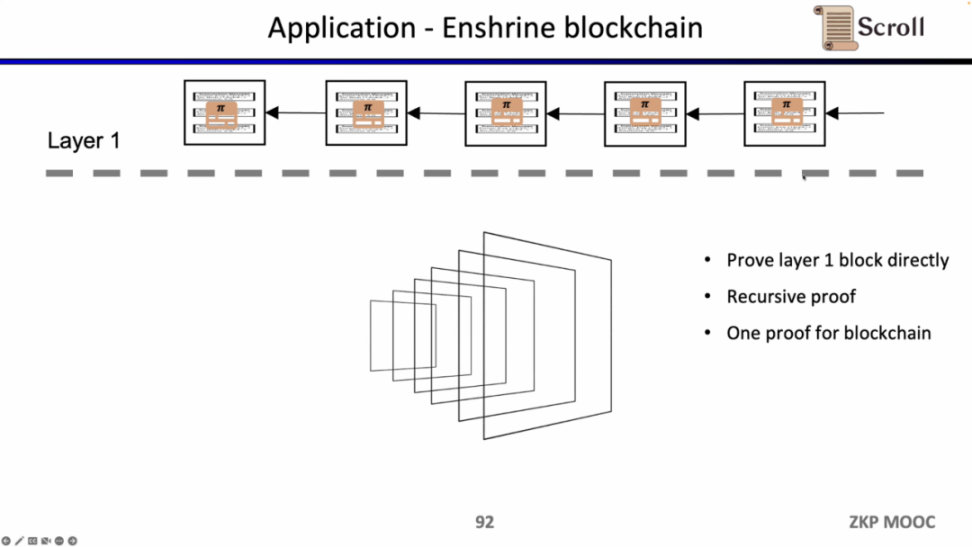
如果我们直接验证 L1 的区块,那么 L1 的节点就不需要重复执行交易,只需要验证每一个区块证明的有效性。这样的架构方案称为 Enshrine Blockchain。目前在以太坊上直接实现难度非常之大,因为需要验证整个以太坊区块,其中会包括验证大量签名,随之带来更长的证明时间和更低的安全性。当然也已经有一些其他公链在通过递归证明,使用单个证明,来验证整个区块链,例如 Mina。
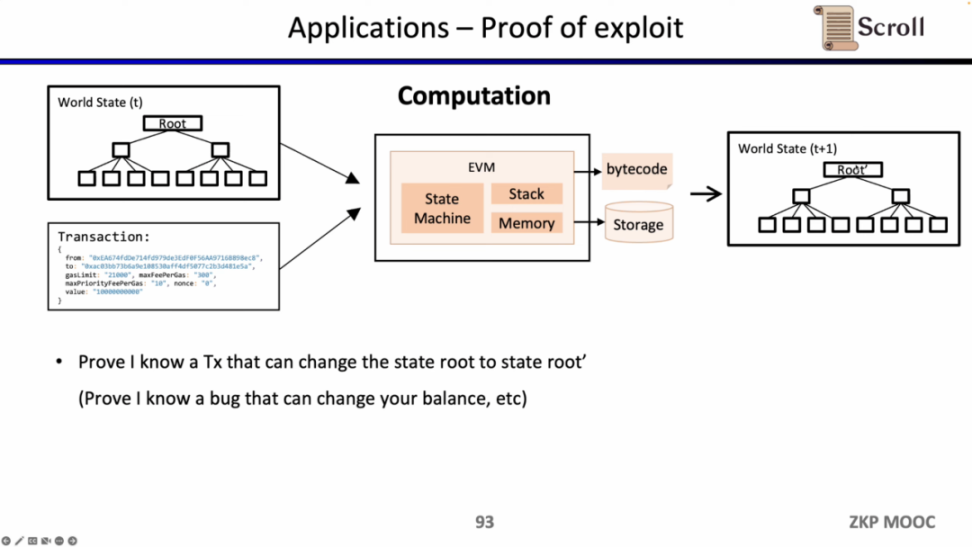
因为 zkEVM 可以证明状态转换,它也可以被白帽所利用,来证明自己知道某些智能合约的漏洞,寻求项目方的赏金。
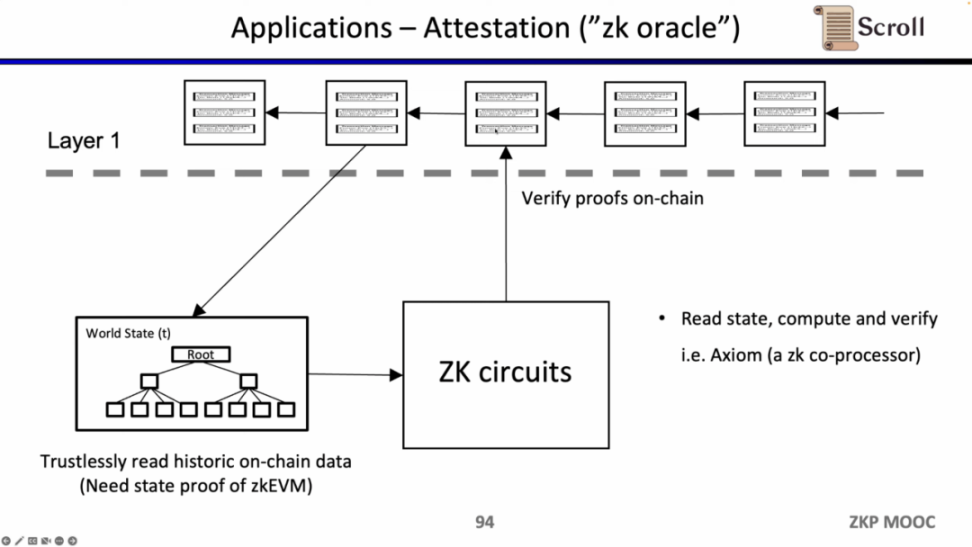
最后一个用例是,是通过零知识证明来证明对历史数据的声明,作为预言机来使用,目前 Axiom 正在做这方面的产品。最近的 ETHBeijing 黑客松上,GasLockR 团队正是利用了这一特性,证明了历史的 Gas 开销。
最后,Scroll 正在构建 zkRollup 的以太坊通用扩容解决方案,使用了非常先进的算术化电路和证明系统,并且通过硬件加速构建快速的验证器,证明递归。目前 Alpha 测试网已经上线,并稳定运行了很长时间。
当然仍然有一些有趣的问题需要解决,包括协议设计和机制设计,零知识工程和实际效率,欢迎大家加入 Scroll 一起构建!

