一个关于 Curve 和 Uniswap 的数学巧合以及它仅仅是个巧合

September 21st, 2023

（本文是「相看两不厌：Uniswap 和 Curve 的比较研究」系列文章的第一篇，作者推特：@observerdq 另，本文是读了 Dan Robinson「Uniswap v3: The Universal AMM」一文后延伸出的思考。）

有一个很妙的发现。

2019年 Curve V1 在构造 AMM 公式时，推演过程中有一个中间形态的公式，而这个公式和一年多后 Uniswap V3 的基础公式恰恰有着相同的结构（前者是后者的一种特殊形态)。

完全不同的思考路径，出现了数学上的交点，妙哉。

本文将从起点梳理 Curve V1 和 Uniswap V3 的构造思考过程，两者在构造过程中数学意义上的擦肩而过，以及是如何地又分道扬镳通向不同的终点。

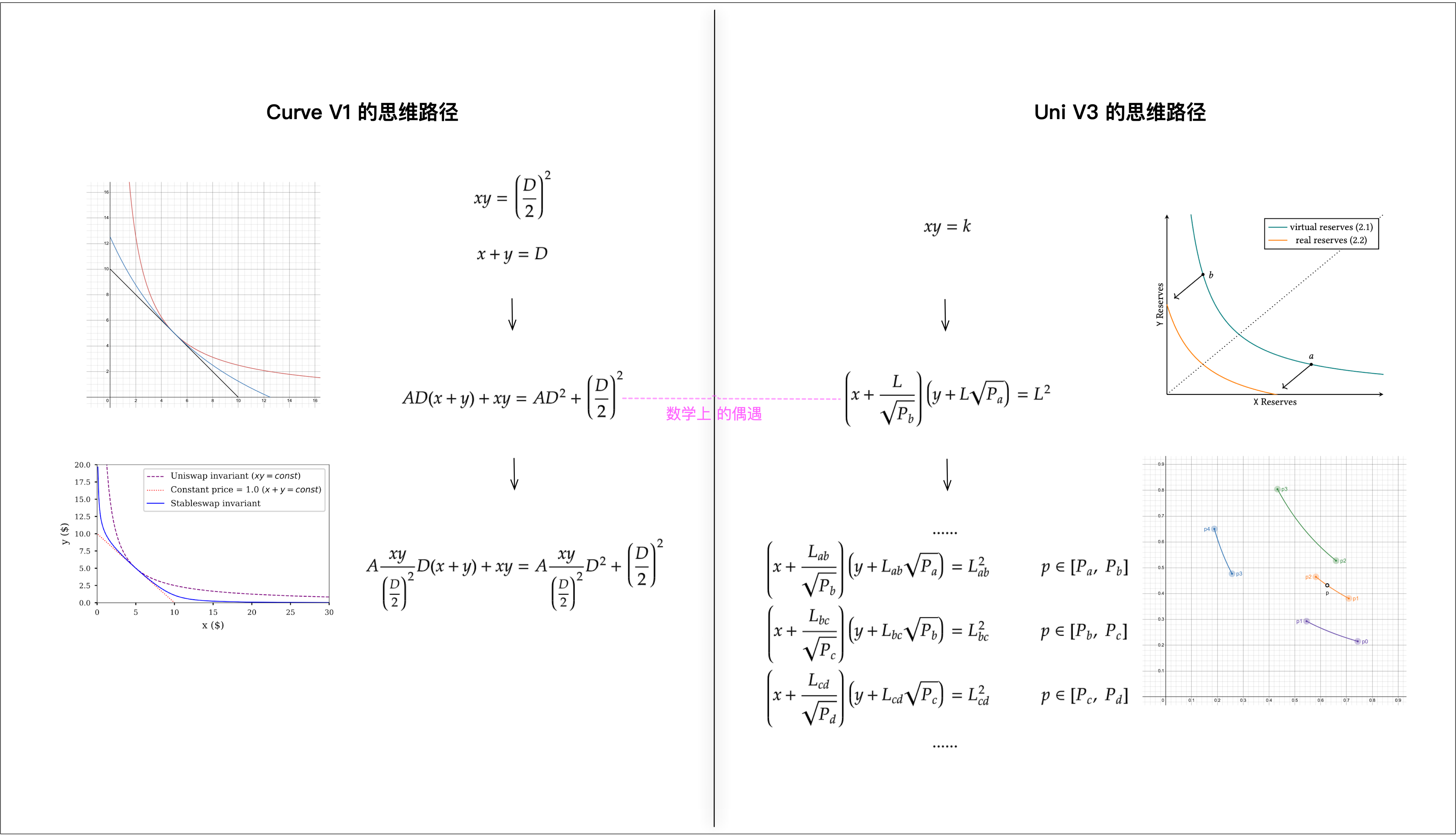
1. Curve V1 公式构建的思维路径

2018年底 Uniswap 的 xy=k 横空出世，是为一次范式革命。但在稳定币交易对的场景下，缺陷显著。Michael 抓住了此切入点，于19年底推出了全新 AMM Curve V1 。

新 AMM 公式构造过程的基础之一仍然是 xy=k。后续将统一按照 Curve V1 白皮书的参数代号，写为如下公式。

xy=(\frac{D}{2})^2

稳定币交易对的价格多数时候只在 1:1 附近很小的区间浮动，只在 1:1 单一价格点提供流动性的公式便是 x+y=D，这是构造过程的另一基础。

Michael 希望将两个基础公式揉合起来，又或者说在 xy=(D/2)**2 的基础之上，引入一些x+y=D 的特性。

于是把两个基础公式「杂交」加到了一起，得到了一个揉合公式。

AD(x+y)+xy=AD^2+(\frac{D}{2})^2

其中 x+y=D 的部分，配上了一个 A 参数，且额外在等号两侧都乘上了 D。乘以 D 的原因，是为了让 A 参数去维度化（不论池子内是两代币、三代币亦或更多，同样的 A 值有同样的效力），这里不展开，也并非本次讨论的重点。

重点在 A 参数。先说明一下，Curve V1 白皮书在揉合公式内使用的是希腊字母 Chi （长得很像 x ），而并非 A。为了书写方便和阅读体验，我改用了 A ，并不会影响论述。

\chi

A 参数的作用，或许可以用黑灰白的色条来类比理解，90%灰就很像黑了，而10%灰就更接近白。A 参数决定了最终的公式产物更像 x+y=D，还是更像 xy=(D/2)**2。

从极限 A 的数值，可以更好理解这个揉合的过程。A = 0，揉合公式就变成了 xy=(D/2)**2。A = 无穷大，揉合公式就变成了 x+y=D。于是 A 在其中，就是一种中间态，A 越大，就越像x+y=D。这种揉合，通过图形可以更加直观地感受，有兴趣可在desmos中玩耍 A。

关于 Curve V1，讲到这里先停住，请大致记住这个揉合公式。然后我们接下去看一下 Uniswap V3 的情况。

2. Uniswap V3 公式构建的思维路径

Uni V1/V2 的 xy=k 称霸江湖后，因「流动性均匀地分布在0至无穷大完整的价格域上」所带来的不足之处日渐显露，Curve V1 的推出更是直接精准地切走了稳定币交易对这一重要的市场。

在设计 V3 时，Uniswap 团队首先想构造出只在有限连续价格区间内提供流动性的公式，他们构造的起点仍然是 xy=k 。

想象一下，如果想实现一个效果，在 [Pa, Pb] 价格区间内（比如 [0.99, 1.01] 或是 [1500, 1700]），这个公式对交易的支持就和 Uni V1/V2 的 xy=k 一模一样，但当价格超出 [Pa, Pb]，就不再提供流动性了。

这种效果对应的公式如下。

(x+\frac{L}{\sqrt{P_b}})(y+L\sqrt{P_a})=L^2

若用图来呈现，会十分清晰，就是把 xy=k 向左下方平移了一些位置。具体要移多少，由Pa、Pb决定。

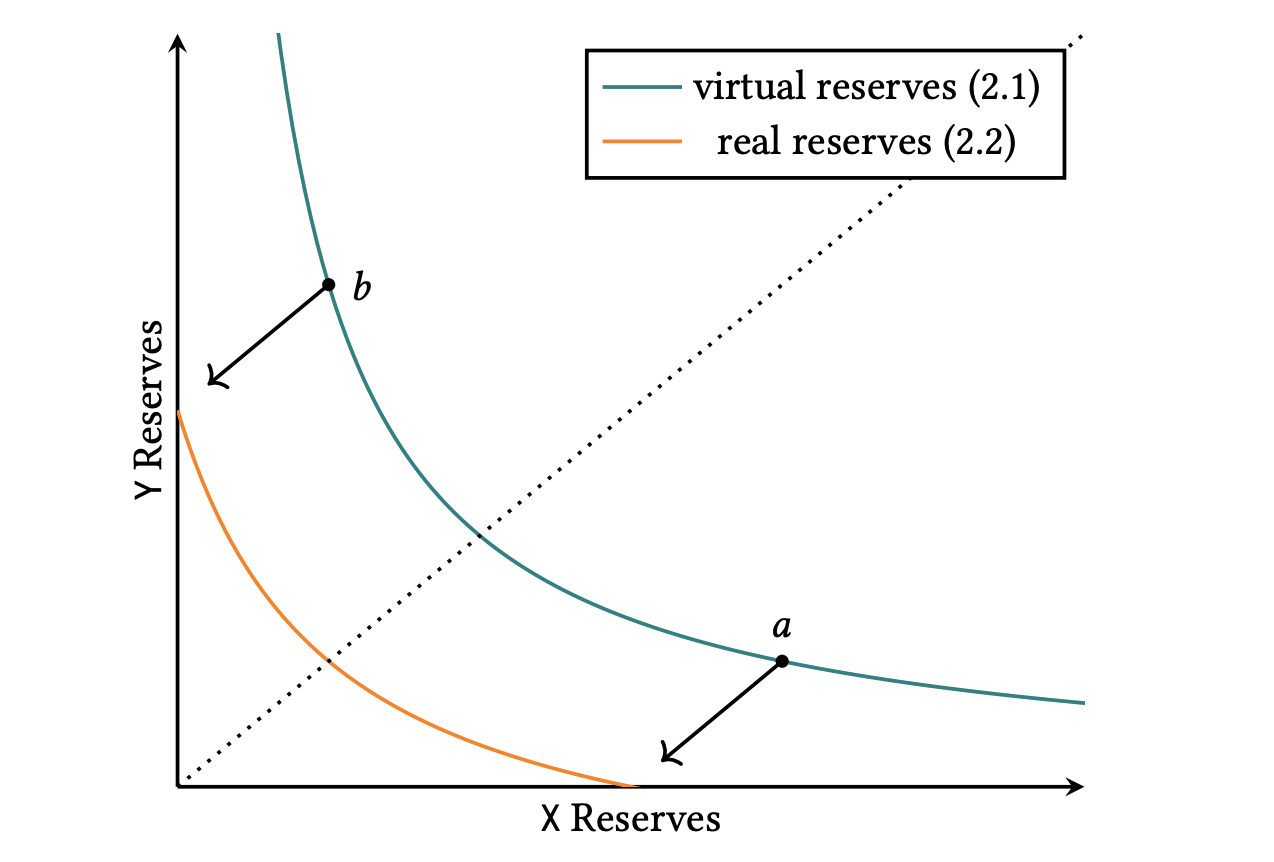
这个公式实现的效果是，所有流动性都集中在 [Pa, Pb] 内，LP 存入一定数量的 X_token 和Y_token，在 [Pa, Pb] 价格区间内提供了一些流动性。单就这个局部的流动性效果，若要让Uni V2 的 LP 来达成，则需要 LP 去存入更多的 X_token 和 Y_token；多的程度取决于 Pa、Pb，可能需要多很多。

这个平移公式是 Uni V3 进一步构造的基础公式，Uni V3 暂讲到这。

3. 奇妙的擦肩而过 - 两种思维路径的交点

将第1节中 Curve V1 的揉合公式做一些变换。

AD(x+y)+xy=AD^2+(\frac{D}{2})^2

(x+AD)(y+AD)=AD^2+(\frac{D}{2})^2+A^2D^2=D^2(A^2+A+\frac{1}{4})=D^2(A+\frac{1}{2})^2

(x+AD)(y+AD)=D^2(A+\frac{1}{2})^2

再和第2节中 Uni V3 的平移公式放在一起观察，会发现两者很像。

(x+\frac{L}{\sqrt{P_b}})(y+L\sqrt{P_a})=L^2

若再对 Uni V3 平移公式内的 Pa 和 Pb 做一些限定，令 Pb=1/Pa，也就是限定价格区间为类似 [0.5, 2] 或 [0.01, 100] 这样的区间，满足在 1:1 价格点两侧倍数意义上的对称。

做了这个限定之后，可以说两个公式就是完全一样了。

(x+AD)(y+AD)=D^2(A+\frac{1}{2})^2

(x+L\sqrt{P_a})(y+L\sqrt{P_a})=L^2

两个公式里有着不同的参数表达，可以很轻松地推导出两组参数的关系。我们不妨以 Curve V1 揉合公式的参数 A 和 D 为基础，计算出 L 和 Pa，如下所示。

L=D(A+\frac{1}{2})=D\frac{2A+1}{2}

\sqrt{P_a}=\frac{AD}{L}=\frac{AD}{D\frac{2A+1}{2}}=\frac{2A}{2A+1}

P_a=(\frac{2A}{2A+1})^2

这些参数的意义和两个协议各自构造的思维路径有关，我们结合两组参数的关系，再简要地回顾一下两种构造过程。

简化起见，假设一个稳定币交易对的池子，初始价格是 1:1。Curve V1 揉合公式中的 D 代表了初始 LP 投入了两种稳定币各 D/2 的数量。A 则代表了这个揉合公式趋近 x+y=D 的程度。

来到 Uni 这一侧，我们再虚拟出一个 Uni V2 的稳定币交易对池子，满足以下公式。

xy=D^2(\frac{2A+1}{2})^2

也就是初始价 1:1 的话，初始 LP 需投入两种稳定币各 D(2A+1)/2 这么多的数量。

这时有一个 Uni V3 池子，希望实现的效果是，只在以下价格区间内提供流动性，

[(\frac{2A}{2A+1})^2,(\frac{2A+1}{2A})^2]

且在这个区间内的流动性效果就如同刚刚虚拟出的 Uni V2 池子那般。满足这个效果的 Uni V3 池子所对应的公式恰恰就和前述的 Curve V1 揉合公式一模一样了。

简要概括的话，Curve V1 通过揉合所实现的效果，恰恰就相当于先虚拟出一个代币储备量大很多（多了 2A 倍）的 Uni V2 池子，然后在 [(2A/(2A+1))**2, ((2A+1)/2A)**2] 价格区间实现了和这个 Uni V2 池子完全相同的流动性效果。

4 分道扬镳 - 两种思维路径的不同终点

Curve V1 揉合公式就是 Uni V3 平移公式的一个特殊形态。事实上，若在 Curve V1 揉合公式内再引入一个参数，x+y 的部分调整为 x+py，两者就完全等价了，这里不多展开。

Curve V1 在揉合公式的基础上，Uni V3 在平移公式的基础上，顺着各自原本的思维路径，继续前行，分道扬镳。

4.1 Curve V1：进一步的动态渐变揉合

Curve V1 揉合公式存在一个缺陷，只在有限价格区间内提供流动性，Michael 需要的是一个全价格区间都有流动性的公式。（至于为什么有这个需求？或许全价格区间都有流动性是很自然的、更加完整健全的状态，比如在对外提供 oracle 的意义上。）

我们可以这么来理解他进一步构造的思路：让这个揉合的程度动态化。之前的揉合公式里的 A 是一个常数，代表了统一的揉合程度。现在进一步地，当 x 偏离 D/2 越多（即 x 越小或越大时），或者说价格偏离 1:1 越多，让揉合的程度更加偏向 xy=(D/2)**2，x 或价格偏离到极限状态时，就变成了单纯的 xy=(D/2)**2，这样就实现了全价格区间都有流动性。

Michael 把 A 变成了 Axy/(D/2)**2，

A\ \ \ ->\ \ \ A\frac{xy}{(\frac{D}{2})^2}

这就可以实现上面所讲的动态渐变效果。构造方式当然不仅限于这一种，我有种感觉 Michael 在这一步构造过程里，并没有对不同的动态渐变实现方式的差异做很深入的对比研究，或许只要能方便地实现全价格流动性就点到为止了。

终于，我们得到了 Curve V1 的最终形态公式如下。

A\frac{xy}{(\frac{D}{2})^2}D(x+y)+xy=A\frac{xy}{(\frac{D}{2})^2}D^2+(\frac{D}{2})^2

4.2 Uni V3：放弃大一统单一公式，自由组合分段函数

Uni V3 平移公式最核心的内涵在于 [Pa, Pb] 这个价格区间。以这个平移公式作为基础，很自然地，Uni V3 走向了一个方向；不同价格区间的流动性可以不同（如果不同价格区间的流动性相同，那就又回到 Uni V2 了）。

在这个大方向上，仍然有不同的设计分叉。一条分叉路，可以由协议定死一个不同价格区间的流动性分配规则，LP 们仍然是同质的，其实 Curve V1 可以看作是这一种类型（价格区间极限小）。

另一条分叉路，所有的决定权全部让渡给 LP 们，LP 们各自独立的决策共同决定了最终流动性在不同价格区间的分配方式。

Uni V3 选择了后者，这个选择极为关键，这让整个市场博弈的元素极大地丰富了起来，价格判断、波动率判断、运气成分等等都卷入了进来，使得流动性市场离充分竞争市场更近了一步。

从数学角度看 Uni V3 的进一步构造，乍一看，像是一种非常规的分段函数。不同的价格区间，对应着不同的 L 值，相应地就是不同的公式，比如以下一个极简的示例。

(x+\frac{L_{ab}}{\sqrt{P_b}})(y+L_{ab}\sqrt{P_a})=L_{ab}^2\ \ \ \ \ p\in [P_a, P_b]

(x+\frac{L_{bc}}{\sqrt{P_c}})(y+L_{bc}\sqrt{P_b})=L_{bc}^2\ \ \ \ \ p\in [P_b, P_c]

事实上，以上可以转化为标准的分段函数，即以 x 来定义子域，子函数为 y 和 x 的一个公式，本文不展开。

5 结语

Curve V1 于2019年底推出，彼时其主要目的就是更好地支持稳定币交易对、填补该市场空白。或许正是这决定了 Michael 的思维路径，重点是以 1:1 价格点对称的结构，并且流动性相对聚拢在 1:1 价格点附近。当 Michael 将 x+y=D 和 xy=(D/2)**2 杂交推导出了揉合公式时，在我看来最核心、最具开创性的工作已经完成，因为这个揉合公式已经满足了上述的对称、聚拢的特征。而将揉合公式进一步改造成支持全价格区间流动性的公式，对 Michael 而言，或许只是略施小计，收尾工作而已。

Uni V3 更晚才推出，2021年3月白皮书发布。Uni 团队已经看到了 Curve V1 的足够长时间的运行情况。一群极聪明的人，回击 Curve 的方法自然要升维。Uni 团队直接打破了一个大前提，LP 们不再「大锅饭」，可以不再统一地按照每个池子的单一固定公式去提供流动性。

Uni V3 在 Uni V1/V2 xy=k 的基础上，构造出了只在特定价格区间提供流动性的一个基础公式（即上文所说的平移公式）。Uni V3 要打破 LP「大锅饭」的大前提，于是赋予了 LP 们以自由，自由地决定在什么样的价格区间（或是数个区间）提供流动性。LP 们每个个体独立自由地决策，汇总到每个池子层面，也会形成一个公式（分段函数），只是这个公式的形状是动态变化的，绝非之前的 AMM 的那种固定形状模式（部分 AMM 可通过治理调整形状，如 Curve V1 调整 A 参数）。

这种设计，不仅仅解决 Uni V2 在稳定币交易对场景下的资金效率低的问题（回击 Curve V1 ），更是在所有的交易对场景，引入了更加充分的竞争，提升了市场整体的资金效率水平。

从历史背景、根本出发点的差异梳理了一遍之后，再来看我最初所感叹的 Curve V1 揉合公式和 Uni V3 平移公式的相似性，又似乎不过是个不值一提的简单数学巧合罢了。

Subscribe to observerdq

Receive the latest updates directly to your inbox.

Mint this entry as an NFT to add it to your collection.

Verification

This entry has been permanently stored onchain and signed by its creator.

Arweave Transaction

75oe_entgbvCnbh…WNgZC15ZA5inZ6k

Author Address

0x111c5b6E316D720…0943Ac0Bb24ffe6

Content Digest

ST3J5KlnBUc3guh…UMJl3BUCgyWN-pc