恒定乘积做市商模型存在的滑点与无常损失饱受诟病,研究员通过数学理论分析和数值模拟来理解该模型的滑点和无常损失的原理和过程。
恒定乘积做市商模型
恒定乘积做市商模型,由Uniswap率先实现并推广,以恒定乘积公式xy=k为基础,使交易对的两种资产数量乘积恒定不变来推进市场交易。虽然Uniswap在DeFi领域开创了新时期的先河,成为了DEX领域的龙头,但恒定乘积做市商模型存在的滑点与无常损失仍饱受诟病。
滑点
什么是滑点,滑点一般指预设成交价位与真实成交价位的偏差。恒定乘积AMM中同样存在滑点,一旦发生交易,池中资产的储备发生变化,资产实际的交易执行价就会发生变化,产生滑点。交易额越大,滑点越大,交易者的损失就越大。
公式分析
根据恒定乘积,当用dx个x兑换dy个y时(忽略手续费),有:
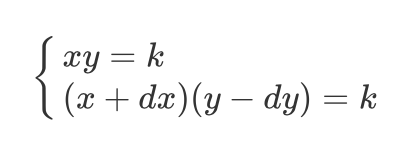
可得,兑换量:
则在实际兑换中,y相对x的单价为:
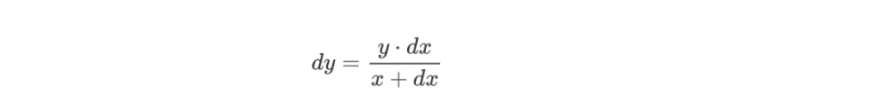
而兑换前,池中的y单价为x/y,那么y单价的滑点就产生了:
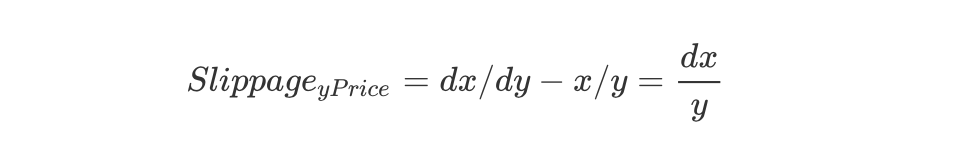
交易量dx越大,产生的滑点就越大,偏离实际价位就越大,而池中的资金储备越多、交易深度越大,则能尽量减少滑点的溢价,使用户的交易损耗降低。
实际计算
Uniswap在实际计算交易滑点时,是通过百分比来显示的:
Uniswap源码中对滑点的计算是在uniswap-v2-sdk/src/entities/trade.ts文件中的computePriceImpact函数中实现的
按照函数中的逻辑,滑点百分比计算公式如下:
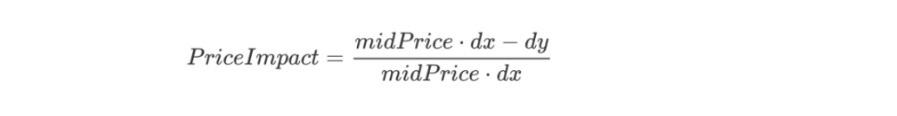
这里的midPrice从代码上看不出是x对y的价格还是y对x的价格,但按照公式的计算逻辑,当midPrice代表x对y的价格时,midPrice·dx就代表理论应得y的数量,那么这个公式就是按照滑点差值/理论应得量的方式计算的
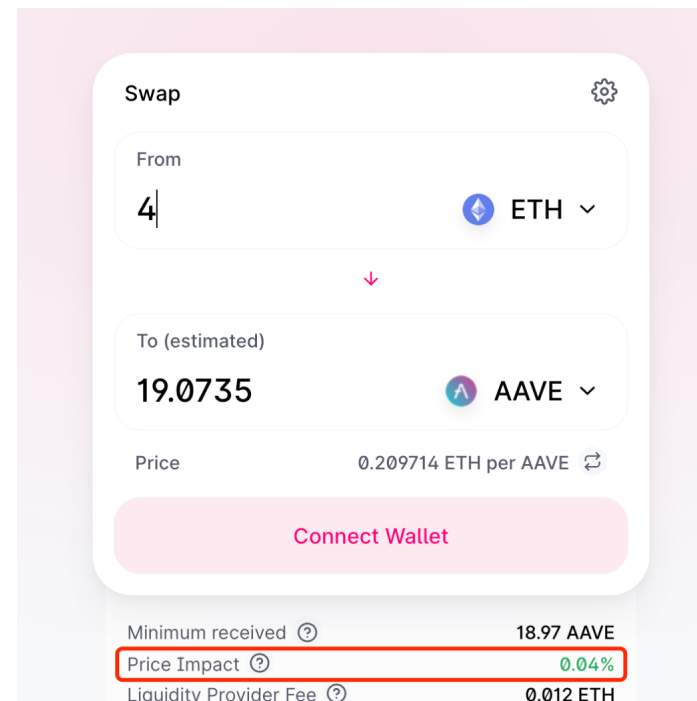
为验证这一点,来到Uniswap界面断点调试,以ETH兑换AAVE为例
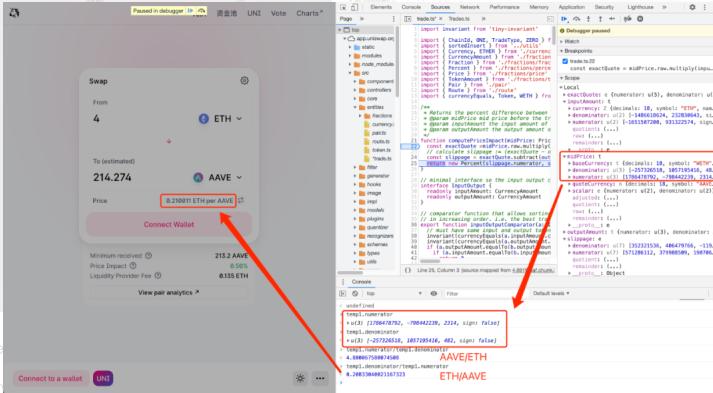
可以看到midPrice实际采用的确实就是前面猜测的x对y的价格,并且是不同于界面中Price所显示实际兑换价的理论价
那么化简公式(2):
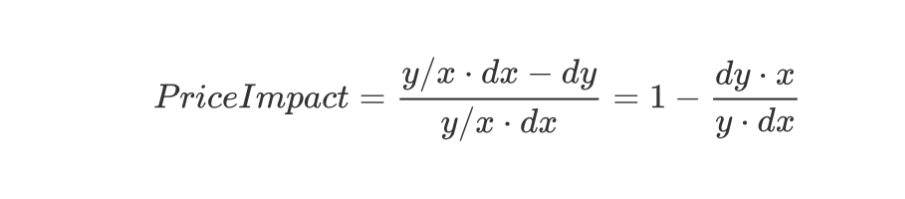
将前面推导的公式(1),带入上式可得:
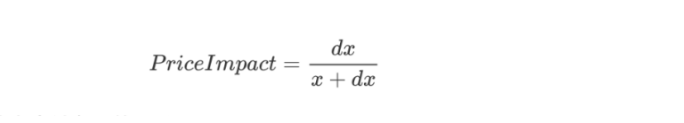
那么滑点百分比即是兑换量占用于兑换的资产储备量的百分比
当然,这里总结出的滑点计算还只是通过AMM机制所算出的理论滑点,实际上滑点还会受很多因素影响,比如网络延时、区块确认等等
无常损失
什么是无常损失,当资产价格剧烈波动时,持有的资产净值损耗减少,就会产生暂时性的账面损失。但如果将资产投入流动性资金池提供流动性,由于AMM的机制,价格与外部市场脱离,并不会自动调整价格,而需要依靠套利者买卖资产来使其达到与外部市场价格的平衡,造成越涨越卖、越跌越买的情况,所以这种套利行为的存在,通常将会使无常损失变成永久性损失。
数值分析
假设现有一恒定乘积做市的DEX,交易对ETH/DAI,流动性为10:400,则当前k=4000,ETH价格为40DAI/ETH
若一流动性供应商,已投入2ETH和80DAI,则流动性占比为20%
当ETH突然上涨,价格到达60DAI/ETH,此时就会有套利者在该DEX用DAI兑换ETH来套利
设共用dy个DAI兑换dx个ETH后,AMM池中ETH:DAI价格达到与外部平衡的1:60
则有:
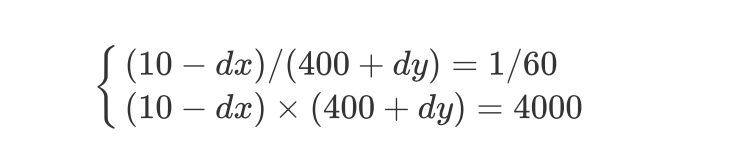
解得:
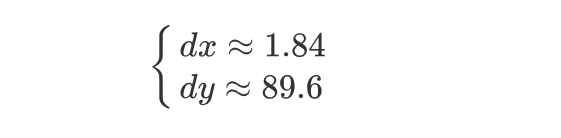
即用89.6DAI兑换1.84ETH进行套利后,池中
ETH:DAI=8.16:489.6≈1:60
套利价为dy/dx≈47.41 DAI/ETH,相比池中价略高,存在滑点;相比池外价略低,即是套利空间
根据之前提供的流动性占比20%,则现在该流动性供应商在池中持有的资产变为ETH:DAI=1.632:97.92
相比套利前,相当于-0.368ETH,+17.92DAI,而ETH按现价60DAI/ETH来算,有-0.368ETH=-22.08DAI,与+17.92DAI不平衡,这就产生了无常损失。
总结
Uniswap的恒定乘积AMM机制简洁、优雅,提供了无限的流动性,但同样也有着滑点、无常损失的不足。