Initialement publié en anglais par StarkWare le 28 mai, 2019.

La Sauce Secrète de la Succinctivité

C’est le quatrième article de notre série STARK Math. Si vous ne l’avez pas encore fait, nous vous recommandons de lire les articles 1 (Le voyage commence), 2 (Arithmétique I) et 3 (Arithmétique II) avant de lire celui-ci. Nous avons expliqué jusqu’ici comment, dans STARK, le processus d’arithmétisation permet de réduire le problème de l’intégrité computationnelle à un problème de test de faible degré.

Le test de faible degré se rapporte au problème de décider si une fonction donnée est un polynôme d’un certain degré limité, en ne faisant qu’un petit nombre de requêtes à la fonction. Les tests de faible degré font l’objet d’études depuis plus de deux décennies et constituent un outil central de la théorie des preuves probabilistes. Le but de cet article est d’expliquer plus en détail les tests de faible degré et de décrire FRI, le protocole que nous utilisons pour les tests de faible degré dans STARK. Ce post suppose une familiarité avec les polynômes sur les champs finis.

Pour rendre cet article très mathématique plus facile à digérer, nous avons marqué certains paragraphes comme ceci :

les paragraphes qui contiennent des preuves ou des explications qui ne sont pas nécessaires pour comprendre le tableau d’ensemble seront marqués comme ceci

Le test de faible degré

Avant d’aborder le test, nous présentons d’abord un problème un peu plus simple comme un échauffement : on nous donne une fonction et on nous demande de décider si cette fonction est égale à un polynôme de degré inférieur à une constante d, en interrogeant la fonction à un «petit» nombre d’emplacements. Formellement, compte-tenu d’un sous-ensemble L d’un champ F et d’un degré lié d, nous voulons déterminer f:L➝F est égal à un polynôme de degré inférieur à d, c’est-à-dire s’il existe un polynôme

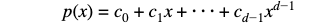
sur F pour laquelle p (a) = f (a) pour chaque a de L. Pour des valeurs concrètes, vous pouvez penser à un champ d’une très grande taille, disons 2¹²⁸, et L qui est d’environ 10 000 000.

Résoudre ce problème nécessite d’interroger f à l’ensemble du domaine L, car f pourrait convenir avec un polynôme partout dans L sauf pour un emplacement unique. Même si nous admettons une probabilité d’erreur constante, le nombre de requêtes sera toujours linéaire dans la taille de L.

Pour cette raison, le problème des tests de faible degré se réfère en fait à un relâchement approximatif du problème ci-dessus, qui suffit pour construire des preuves probabilistes et peut également être résolu avec un nombre de requêtes logarithmiques en |L| (notez que si L≈10,000,000, alors log2 (L) ≈23). De manière plus détaillée, nous souhaitons faire une distinction entre les deux cas suivants.

• La fonction f est égale à un polynôme de degré faible. A savoir, il existe un polynôme p(x) sur F, de degré inférieur à d, qui est en accord avec f partout sur L.
• La fonction f est loin de TOUS les polynômes de degré faible. Par exemple, nous devons modifier au moins 10% des valeurs de f avant d’obtenir une fonction qui est en accord avec un polynôme de degré inférieur à d.

Notez qu’il y a une autre possibilité – la fonction f peut être légèrement proche d’un polynôme de faible degré, mais pas égale à un. Par exemple, une fonction dont 5% des valeurs diffèrent d’un polynôme de faible degré ne tombe dans aucun des deux cas décrits ci-dessus. Cependant, l’étape d’arithmétisation préalable (dont il a été question dans nos articles précédents) garantit que le troisième cas ne se produira jamais. De façon plus détaillée, l’arithmétisation montre qu’un test honnête traitant une affirmation vraie aboutira dans le premier cas, alors qu’un test (éventuellement malveillant) essayant de « prouver » une affirmation fausse aboutira, avec une forte probabilité, dans le second cas.

Afin de distinguer les deux cas, nous utiliserons un test polynomial-time probabiliste qui interroge f à un petit nombre d’emplacements (nous discuterons plus loin de ce que « petit » signifie).

Si f est effectivement de faible degré, alors le test devrait accepter avec une probabilité 1. Si, au contraire, f est loin d’être faible, alors l’essai devrait être rejeté avec une probabilité élevée. Plus généralement, nous recherchons la garantie que si f est δ-loin de toute fonction de degré inférieur à d (càd, il faut modifier au moins δ|L| emplacements pour obtenir un polynôme de degré inférieur à d), alors le test rejette avec probabilité au moins Ω (δ) (ou une autre fonction « nice » de δ). Intuitivement, plus δ est proche de zéro, plus il est difficile de distinguer les deux cas.

Dans les sections qui suivent, nous décrivons un test simple, puis nous expliquons pourquoi il ne suffit pas dans notre contexte, et enfin nous décrivons un test plus complexe qui est exponentiellement plus efficace. Ce dernier test est celui que nous utilisons dans STARK.

Le test direct

Le premier test que nous considérons est simple : il teste si une fonction est (proche de) un polynôme de degré inférieur à d, en utilisant des requêtes d+1. Le test repose sur un fait fondamental au sujet des polynômes : tout polynôme de degré inférieur à d est entièrement déterminé par ses valeurs à n’importe quel emplacement de d distinct de F. Ce fait est une conséquence directe du fait qu’un polynôme de degré k peut avoir tout au plus k racines en F. Il est important de noter que le nombre de requêtes, qui est d+1, peut être significativement inférieur à la taille du domaine de f, qui est |L|.

Nous abordons d’abord deux cas particuliers simples, afin de construire une intuition sur la façon dont le test fonctionnera dans le cas général.

• Le cas d’une fonction constante (d=1). Ceci correspond au problème de la distinction entre le cas où f est une fonction constante (f(x) =c pour certains c en F), et le cas où f est loin de toute fonction constante. Dans ce cas particulier, il y a un test naturel de 2 requêtes qui pourrait fonctionner : requête f à un emplacement fixe z1 et aussi à un emplacement aléatoire w, puis vérifiez que f(z1) =f(w). Intuitivement, f(z1) détermine la constante (présumée) de f, et f (w) teste si la totalité de f est proche de cette constante ou non.
• Le cas d’une fonction linéaire (d=2). Ceci correspond au problème de la distinction entre le cas où f est une fonction linéaire (f(x) =ax+b pour certains a,b en F), et le cas où f est loin de toute fonction linéaire. Dans ce cas particulier, il y a un test naturel de 3-requêtes qui pourrait fonctionner : requête f à deux emplacements fixes z1,z2 et aussi à un emplacement aléatoire w, puis vérifier que (z1,f (z1)), (z2,f (z2)), (w,f (w)) sont colinéaires, c’est-à-dire que nous pouvons tracer une ligne à travers ces points. Intuitivement, les valeurs de f(z1) et f(z2) déterminent la droite (présumée), et f(w) teste si la totalité de f est proche de cette droite ou non.

Les cas particuliers ci-dessus suggèrent un test pour le cas général d’un degré lié d. Requête f à d emplacements fixes z1,z2,...,zd et aussi à un emplacement aléatoire w. Les valeurs de f à z0,z1,...,zd définissent un polynôme h(x) unique de degré inférieur à d sur F qui est en accord avec f à ces points. Le test vérifie alors que h(w) =f(w). Nous appelons cela le test direct.

Par définition, si f(x) est égal à un polynôme p(x) de degré inférieur à d, alors h(x) sera identique à p(x) et donc le test direct réussit avec la probabilité 1. Cette propriété est appelée «perfect completeness», et cela signifie que ce test n’a qu’une erreur unilatérale.

Nous sommes laissés à argumenter ce qui se passe si f est δ-loin de toute fonction de degré inférieur à d. (Par exemple, pensez à δ=10%.) Nous soutenons maintenant que, dans ce cas, le test direct rejette avec probabilité au moins δ. En effet, prenons μ la probabilité, sur un choix aléatoire de w, que h (w)≠f (w). Noter que μ doit être au moins δ.

C’est parce que si nous supposons vers la contradiction que μ est plus petit que δ, alors nous déduisons que f est δ-proche de h, ce qui contredit notre hypothèse que f est δ-loin de toute fonction de degré inférieur à d.

Le test direct ne suffit pas pour nous

Dans notre contexte, nous nous intéressons à tester les fonctions f:L➝F qui encodent les traces de calcul, et dont le degré d (et le domaine L) est assez grand. Le simple fait d’exécuter le test direct, qui fait des requêtes d+1, serait trop coûteux. Afin d’obtenir les économies exponentielles de STARK (en temps de vérification comparé à la taille de la trace de calcul), nous devons résoudre ce problème avec seulement des requêtes O(log d), qui est exponentiellement inférieur au degré lié d.

Ceci, malheureusement, est impossible car si nous interrogeons f à des emplacements inférieurs à d+1, alors nous ne pouvons rien conclure.

Une façon de voir ceci est d’examiner deux distributions différentes de fonctions f:L➝F. Dans une distribution nous choisissons uniformément un polynôme de même degré d et l’évaluons sur L. Dans l’autre distribution, nous choisissons uniformément un polynôme de degré inférieur à d et nous l’évaluons sur L. Dans les deux cas, pour n’importe quel emplacement d z1,z2,…,zd, les valeurs f(z1),f(z2),…,f(zd) sont distribuées uniformément et indépendamment. (Nous laissons ce fait à titre d’exercice pour le lecteur.) Ceci implique qu’en théorie de l’information nous ne pouvons pas distinguer ces deux cas, même si un test est nécessaire (puisque les polynômes de la première distribution doivent être acceptés par le test alors que ceux de degré exactement d sont très éloignés de tous les polynômes de degré inférieur à d, et doivent donc être rejetés).

Il semble que nous ayons un défi difficile à relever.

Un Prouver vient à la rescousse

Nous avons vu qu’il nous faut des requêtes d+1 pour tester qu’une fonction f:L➝F est proche d’un polynôme de degré inférieur à d, mais nous ne pouvons pas nous permettre autant de requêtes. Nous évitons cette limitation en considérant un cadre légèrement différent, ce qui nous suffit. Plus précisément, nous considérons le problème des essais à faible degré lorsqu’un prouveur est disponible pour fournir des informations auxiliaires utiles sur la fonction f. Nous verrons que dans ce cadre de test de faible degré, nous pouvons obtenir une amélioration exponentielle du nombre de requêtes, jusqu’à O(log d).

Plus en détail, nous considérons un protocole mené entre un prouveur et un vérifieur, dans lequel le prouveur (non fiable) tente de convaincre le vérifieur que la fonction est de faible degré. D’une part, le prouveur connaît toute la fonction f testée. D’un autre côté, le vérifieur peut interroger la fonction f à un petit nombre d’emplacements, et est prêt à recevoir l’aide du proveur, mais ne fait PAS confiance à l’honnêteté du prouveur. Cela signifie que le prouveur peut tricher et ne pas suivre le protocole. Cependant, si le prouveur triche, le vérifieur a la liberté de «rejeter», que la fonction f soit de faible degré ou non. Le point important ici est que le vérifieur ne sera pas convaincu que f est faible si ce n’est pas vrai.

Notez que le test direct décrit ci-dessus est simplement le cas particulier d’un protocole dans lequel le prouveur ne fait rien, et le vérifieur teste la fonction sans assistance. Pour faire mieux que le test direct, nous devrons tirer parti de l’aide du prouveur d’une manière significative.

Tout au long du protocole, le prouveur voudra permettre au vérifieur d’interroger des fonctions auxiliaires sur des emplacements de son choix. Cela peut se faire par le biais d’engagements, un mécanisme dont nous parlerons dans un prochain article. Pour l’instant, il suffit de dire que le testeur peut valider une fonction de son choix via une arborescence Merkle, et ensuite le vérifieur peut demander au testeur de révéler n’importe quel ensemble d’emplacements de la fonction validée. La principale propriété de ce mécanisme d’engagement est qu’une fois que le prouveur s’engage sur une fonction, il doit révéler les valeurs correctes et ne peut pas tricher (par exemple, il ne peut pas décider quelles sont les valeurs de la fonction après avoir vu les requêtes du vérifieur).

Réduire de moitié le nombre de requêtes pour le cas de deux polynômes

Commençons par un exemple simple qui illustre comment un prouveur peut aider à réduire le nombre de requêtes d’un facteur 2. Nous nous baserons sur cet exemple plus tard. Supposons que nous ayons deux polynômes f et g et que nous voulons tester qu’ils sont tous deux de degré inférieur à d. Si nous exécutons simplement le test direct individuellement sur f et g alors nous aurions besoin de faire 2 * (d + 1) requêtes. Nous décrivons ci-dessous comment, à l’aide d’un prouveur, nous pouvons réduire le nombre de requêtes à (d + 1) plus un terme d’ordre plus petit.

Tout d’abord, le vérifieur prélève une valeur aléatoire α du champ et l’envoie au prouveur. Ensuite, le prouveur répond en s’engageant à l’évaluation sur le domaine L (rappelons que L est le domaine de la fonction f) du polynôme h(x) = f(x) + 𝛼 g(x) (en d’autres termes, le prouveur calculera et enverra la racine d’un arbre de Merkle dont les feuilles sont les valeurs de h sur L). Le vérifieur teste maintenant que h a un degré inférieur à d, via le test direct, qui nécessite des requêtes d+1.

Intuitivement, si f ou g a un degré d’au moins d, alors avec une forte probabilité h fait de même. Par exemple, considérons le cas où le coefficient de xⁿ dans f n’est pas nul pour n≥d. Ensuite, il y a tout au plus un choix de α (envoyé par le vérifieur) pour lequel le coefficient de xⁿ en h est zéro, ce qui signifie que la probabilité que h ait un degré inférieur à d est approximativement 1/|F| Si le champ est suffisamment grand (par exemple, |F|>2¹²⁸), la probabilité d’erreur est négligeable.

Mais la situation n’est pas aussi simple. La raison en est que, comme nous l’avons expliqué, nous ne pouvons pas littéralement vérifier que h est un polynôme de degré inférieur à d. Au lieu de cela, nous pouvons seulement vérifier que h est proche d’un tel polynôme. Cela signifie que l’analyse ci-dessus n’est pas exacte. Est-il possible que f soit loin d’un polynôme de faible degré et que la combinaison linéaire h soit proche d’une avec une probabilité non négligeable sur α? Dans des conditions modérées, la réponse est non (c’est ce que nous voulons), mais elle n’entre pas dans le cadre du présent article; nous renvoyons les lecteurs intéressé à cet article et à celui-ci.

De plus, comment le vérifieur sait-il que le polynôme h envoyé par le prouveur a la forme f(x)+𝛼 g(x)? Un testeur malveillant peut tricher en envoyant un polynôme qui est certes de faible degré, mais qui est différent de la combinaison linéaire demandée par le vérifieur. Si nous savons déjà que h est proche d’un polynôme de faible degré, alors tester que ce polynôme de faible degré a la bonne forme est simple : le vérifieur échantillonne un emplacement z dans L au hasard, interroge f, g, h à z, et vérifie que l’équation h(z)=f(z)+𝛼 g(z) tient. Ce test devrait être répété plusieurs fois pour augmenter la précision du test, mais l’erreur diminue exponentiellement avec le nombre d’échantillons que nous faisons. Cette étape n’augmente donc le nombre de requêtes (qui jusqu’à présent était d+1) que d’un terme d’ordre plus petit.

Diviser un polynôme en deux polynômes plus petits

Nous avons vu qu’avec l’aide du prouveur, nous pouvons tester que deux polynômes sont de degré inférieur à d avec moins de 2* (d+1) requêtes. Nous décrivons maintenant comment nous pouvons transformer un polynôme de degré inférieur à d en deux polynômes de degré inférieur à d/2.

Supposons que f(x) soit un polynôme de degré inférieur à d et supposons que d est pair (dans notre arrangement cela vient sans perte de généralité). On peut écrire f(x) =g(x2)+xh(x2) pour deux polynômes g(x) et h(x) de degré inférieur à d/2. En effet, on peut considérer g(x) comme le polynôme obtenu à partir des coefficients pairs de f(x), et h(x) comme le polynôme obtenu à partir des coefficients impairs de f(x). Par exemple, si d=6, nous pouvons écrire

ce qui signifie que

et

qui est un algorithme n*log (n) pour l’évaluation polynomiale (amélioration par rapport à l’algorithme naïf n2).

Le Protocole FRI

Nous combinons maintenant les deux idées ci-dessus (tester deux polynômes avec la moitié des requêtes, et diviser un polynôme en deux plus petites) dans un protocole qui utilise uniquement les requêtes O(log d) pour tester qu’une fonction f a (plus précisément, est proche d’une fonction de) degré inférieur à d. Ce protocole est connu sous le nom de FRI (qui signifie Fast Reed – Solomon Interactive Oracle Proof of Proximity), et le lecteur intéressé peut en savoir plus ici. Par souci de simplicité, nous supposons ci-dessous que d est une puissance de 2. Le protocole se compose de deux phases: une phase de validation et une phase de requête.

Phase d’engagement

Le prouveur divise le polynôme original f0(x) =f(x) en deux polynômes de degré inférieur à d/2, g₀(x) et h₀(x),, ce qui donne f₀(x)=g₀(x²)+xh₀(x²). Le vérifieur échantillonne une valeur aléatoire α0, l’envoie au prouveur, et lui demande de valider le polynôme f₁(x)=g₀(x) + 𝛼₀h₀(x). Notez que f₁(x) est de degré inférieur à d/2.

Nous pouvons continuer récursivement en divisant f₁(x) en g₁(x) et h₁(x), puis en choisissant une valeur 𝛼₁, en construisant f₂(x) et ainsi de suite. Chaque fois, le degré du polynôme est réduit de moitié. Par conséquent, après les étapes log(d), il nous reste un polynôme constant, et le testeur peut simplement envoyer la valeur constante au vérifieur.

Une note à propos des domaines : pour que le protocole ci-dessus fonctionne, nous avons besoin de la propriété que pour chaque z du domaine L, il maintient que -z est aussi en L. De plus, l’engagement sur f1(x) ne sera pas au-dessus de L mais au-dessus deL²={x²: x ∊ L}. Puisque nous appliquons itérativement l’étape FRI, L² devra également satisfaire la propriété {z,-z}, et ainsi de suite. Ces exigences algébriques naturelles sont facilement satisfaites par des choix naturels de domaines L (disons, un sous-groupe multiplicatif dont la taille est une puissance de 2) et coïncident en fait avec celles dont nous avons besoin pour bénéficier d’algorithmes FFT efficaces (utilisés ailleurs dans STARK, par exemple pour encoder les traces d’exécution).

Phase de requête

Nous devons maintenant vérifier que le prouveur n’a pas triché. Le vérifieur échantillonne un z aléatoire dans L et interroge f0(z) et f0(-z). Ces deux valeurs suffisent à déterminer les valeurs de g₀(z²) et h₀(z²), comme le montrent les deux équations linéaires suivantes pour les deux «variables» g₀(z²) and h₀(z²) :

Le vérifieur peut résoudre ce système d’équations et en déduire les valeurs de g₀(z²) et h₀(z²). Il s’ensuit qu’il peut calculer la valeur de f₁(z²) qui est une combinaison linéaire des deux. Maintenant le vérifieur interroge f₁(z²) et s’assure qu’il est égal à la valeur calculée ci-dessus. Ceci indique que l’engagement à f₁(x), qui a été envoyé par le testeur pendant la phase de propagation, est bien le bon. Le vérifieur peut continuer, en interrogeant f₁(-z²) (rappelons que (-z²)∊ L² et que l’engagement sur f₁(x) a été donné sur L²) et en déduire f₂(z⁴).

Le vérifieur continue ainsi jusqu’à ce qu’il utilise toutes ces requêtes pour finalement déduire la valeur de f_{log d}(z) (notant f avec un subscript log d, que nous ne pouvons pas écrire à cause du manque de support de Medium pour la notation mathématique à part entière). Mais rappelez-vous que f_{log d} (z) est un polynôme constant dont la valeur constante a été envoyée par le testeur en phase de propagation, avant de choisir z. Le vérifieur doit vérifier que la valeur envoyée par le prouveur est bien égale à la valeur calculée par le vérifieur à partir des requêtes aux fonctions précédentes.

Dans l’ensemble, le nombre de requêtes n’est que logarithmique dans le degré lié d.

Pour avoir une idée de pourquoi le testeur ne peut pas tricher, considérez le problème du jouet où f₀ est zéro sur 90% des paires de la forme {z,-z}, c’est-à-dire f₀(z) = f₀(-z) = 0 (appelons-les «bonnes» paires), et non nul sur les 10% restants (les «mauvaises» paires). Avec une probabilité de 10%, le z sélectionné au hasard tombe dans une mauvaise paire. Notez qu’un seul α conduira à f₁(z²)=0, et le reste conduira à f₁(z²)≠0. Si le prouveur triche sur la valeur de f₁(z²), il sera attrapé, donc nous supposons le contraire. Ainsi, avec une probabilité élevée (f₁(z²), f₁(-z²)) sera également une mauvaise paire dans la couche suivante (la valeur de f1 (-z2) n’est pas importante comme f₁(z²)≠0). Cela continue jusqu’au dernier calque où la valeur sera non nulle avec une probabilité élevée.

Par contre, puisque nous avons commencé avec une fonction à 90% de zéros, il est peu probable que le testeur puisse se rapprocher d’un polynôme de faible degré autre que le polynôme zéro (nous ne le prouverons pas ici). En particulier, cela implique que le testeur doit envoyer 0 comme valeur de la dernière couche. Mais alors, le vérifieur a une probabilité d’environ 10% d’attraper le prouveur. Ce n’était qu’un argument informel, le lecteur intéressé peut trouver ici une preuve rigoureuse.

Dans le test décrit jusqu’à présent (et dans l’analyse ci-dessus), la probabilité que le vérifieur attrape un prouveur malveillant n’est que de 10%. En d’autres termes, la probabilité d’erreur est de 90%. Ceci peut être amélioré de façon exponentielle en répétant la phase de requête ci-dessus pour quelques z échantillonnés indépendamment. Par exemple, en choisissant 850z, nous obtenons une probabilité d’erreur de 2^{-128} qui est pratiquement nulle.

Récapitulation

Dans ce post, nous avons décrit le problème des tests de faible degré. La solution directe (test) nécessite trop de requêtes pour obtenir la concision requise par STARK. Pour atteindre la complexité logarithmique des requêtes, nous utilisons un protocole interactif appelé FRI, dans lequel le prouver ajoute plus d’informations afin de convaincre le vérifieur que la fonction est effectivement de faible degré. Essentiellement, FRI permet au vérifieur de résoudre le problème de test de faible degré avec un certain nombre de requêtes (et de rondes d’interaction) qui est logarithmique dans le degré prescrit. L’article suivant résume les trois derniers articles et explique comment supprimer l’aspect interactif utilisé dans FRI et dans les parties précédentes du protocole, afin d’obtenir des preuves succinctes non interactives.

Alessandro Chiesa & Lior Goldberg
StarkWare

Traduction faite par @cleminso