在 DeFi 中,很重要的一点是**“如何为用户寻找最优报价”**。目前市场中有很多 DeFi 协议,不同的协议有自己独特的算法,其流动性源相对独立,使得对于相同的币种,不同的池子会有不同的报价。DEX 通过设计自己的算法、吸引 LP 以期获得更好的报价,如 1inch、0x 等聚合器则选择了另一条路:通过搜索不同池子构成的路径,在 gas 可控的情况下,为用户寻找最优的报价。
随着市场发展,1inch、0x 等聚合器也会有自己独有的报价源,balancer、uniswap V3 等 DEX 也会将用户的一笔交易拆分到多路径中完成,区别在于 DEX 的聚合算法仅基于自己的报价池,而聚合器则充分利用了 DeFi 的可组合性,不仅接入自己的池子,也会接入其他 DEX 的池子,最大化的利用全链的流动性源,以期为用户提供最好的报价。
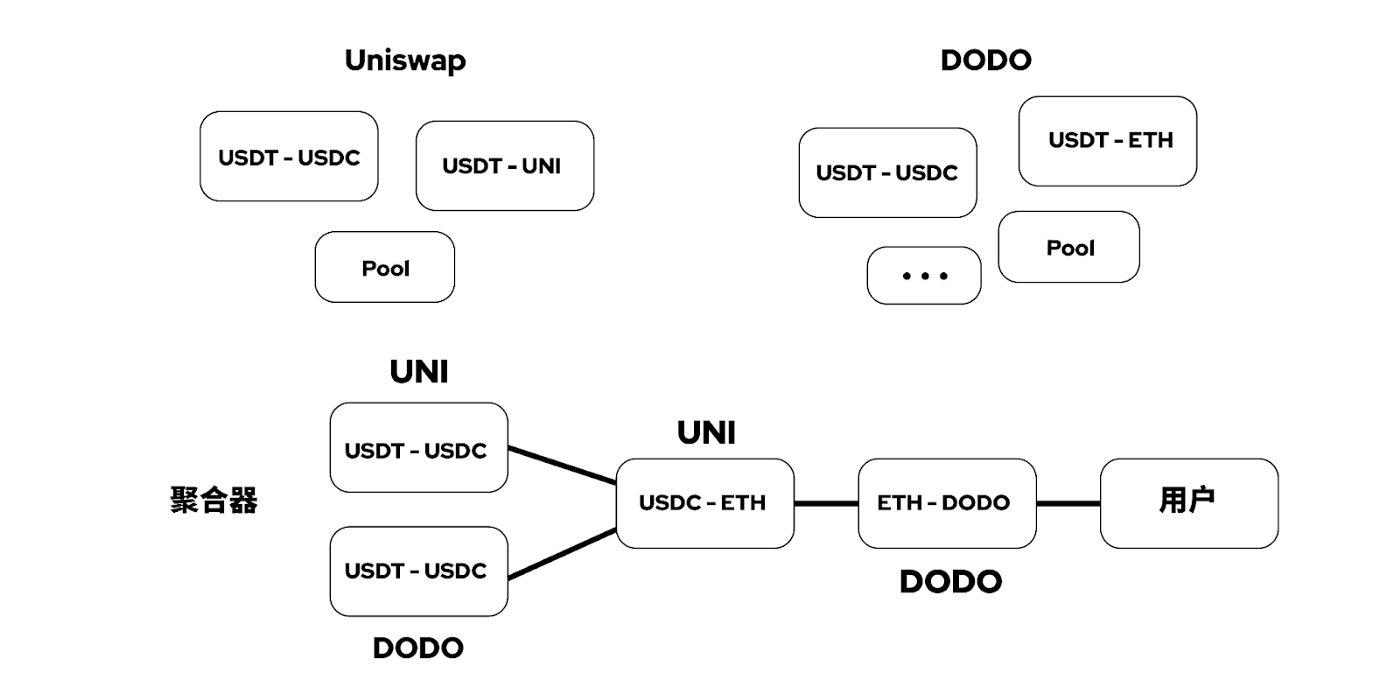
**DODO 一直致力于为用户提供最好的交易体验,除了发展自己的 PMM 池子,DODO 也独立开发了自己的聚合算法。**DODO 的聚合算法并非 Uniswap 等 DEX 内部的拆单路由算法,而是类似 1inch、0x 一样的聚合算法。不仅会接入 DODO 自己的池子,也会接入其他 DEX 的池子,以更好地利用流动性。
这篇文章将分为两部分,本篇将先介绍聚合问题的模型建立,下篇会介绍 DODO 自己的聚合器算法并分析聚合器工程设计上的难点。
1. 建模介绍与解法分析
对一个问题进行合理的建模是解决一个问题的良好开端。首先考虑一个最简单的问题:线性路由。
1.1 线性路由
线性路由指在寻找交易路径的过程中,一交易对只经过一个池子,在此基础上寻找目标token报价最优的路径。例如用户需要交易 ETH-USDC,线性路由所找到的最优路径为 ETH-USDT-USDC,而非[A-C-B]+[A-D-B](即A资产不会拆分为两部分选择不同的路)最终的路径只经过两个池子;这两个池子可能来自不同协议,例如,ETH-USDT 是 Uniswap V3 的池子,USDT-USDC 是 Curve V1 的池子。这种路由模型也是 Uniswap V2、Pancake 等 DEX 使用的路由模型,不同的是他们的流动性源仅为自己的交易所,即 Uniswap V2 路由只会经过 Uniswap V2 的池子,Pancake 的路由只会经过 Pancake 的池子。
我们约定,用户需要卖出的 token 为 fromToken,期望买入的 token 为 toToken,对于任意池子,定义 baseToken 为卖出 token,quoteToken 为买入 token,则可以对于路由路径,第一个池子的baseToken 一定为 fromToken,最后一个池的 quoteToken 一定为 toToken。如图所示:
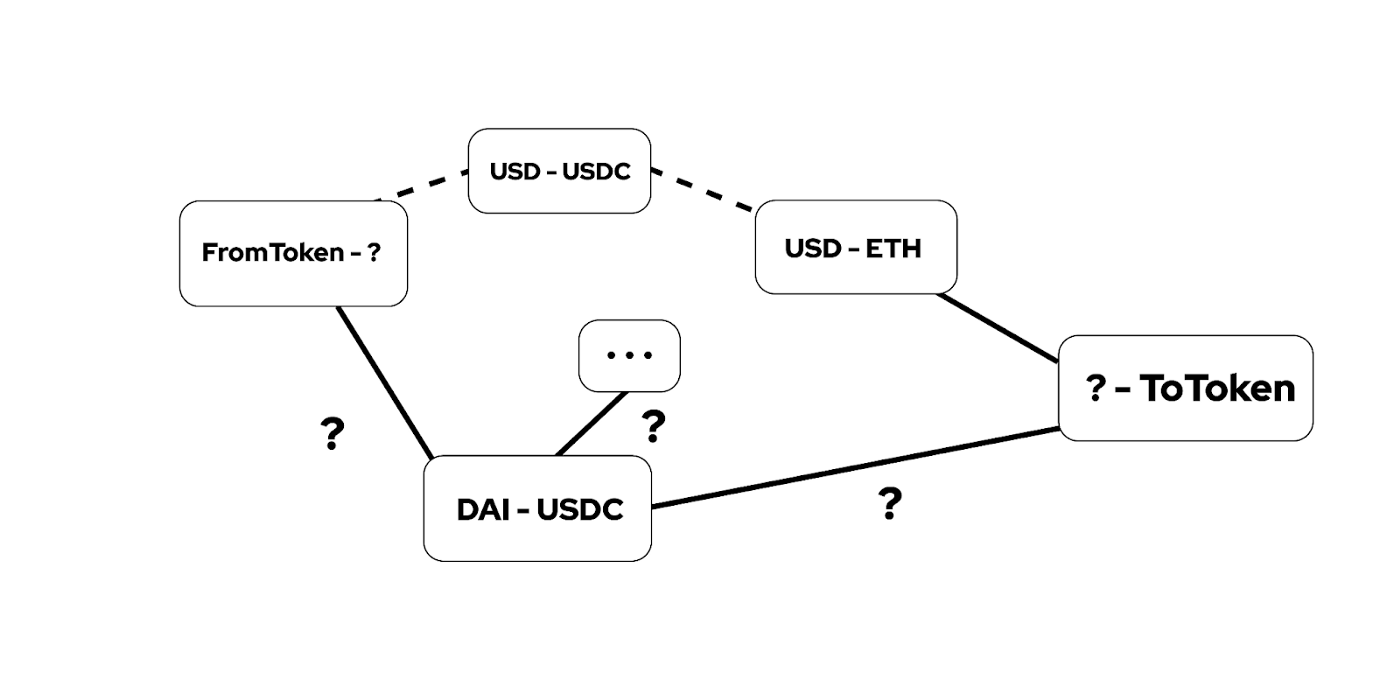
可以将其直接归纳为一个最值问题:设有 n 种不同资产,共有 k 种不同的池子,每个池子所交换的代币数量可以用一组函数表示:
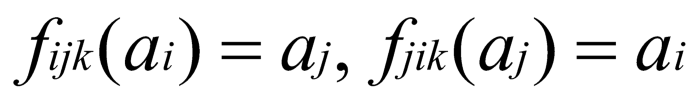
由于所有的 3-token 或多 token 池均可用双 token 池表示,函数可进一步简写为:
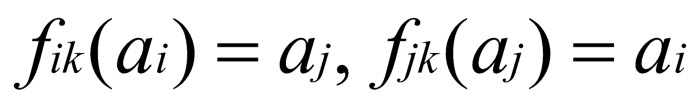
其中 ai 表示第 i 种资产的数量,aj 表示第 j 种资产的数量,k 表示池子编号。设用户 fromToken 数量为 af,最终能得到的 toToken 数量 at, 中途交换的代币集为:
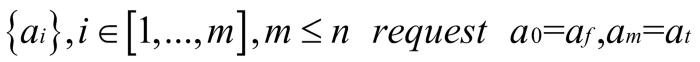
经过 m−1 个池子,记池子为:
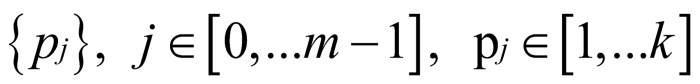
则:
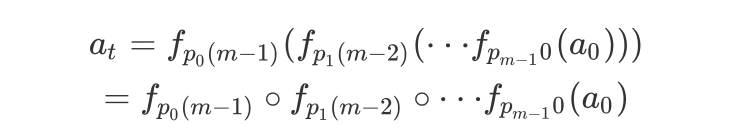
如能求出以上问题的解,即能求出最优路径。
该建模还是太抽象,借助图论,我们可以构建另一种模型。将币种看为节点,baseToken 为 i、quoteToken 为 j 的池子可以构建两条边,从 i 到 j 的边 ρⁱʲᵏ,从 j 到 i 的边 ρʲⁱᵏ, 边权重设为 a0 除以该池子换取的 quoteToken 数量 aj,α₀/αⱼ 则可建立以下含多重边与环的有向图,如下所示:
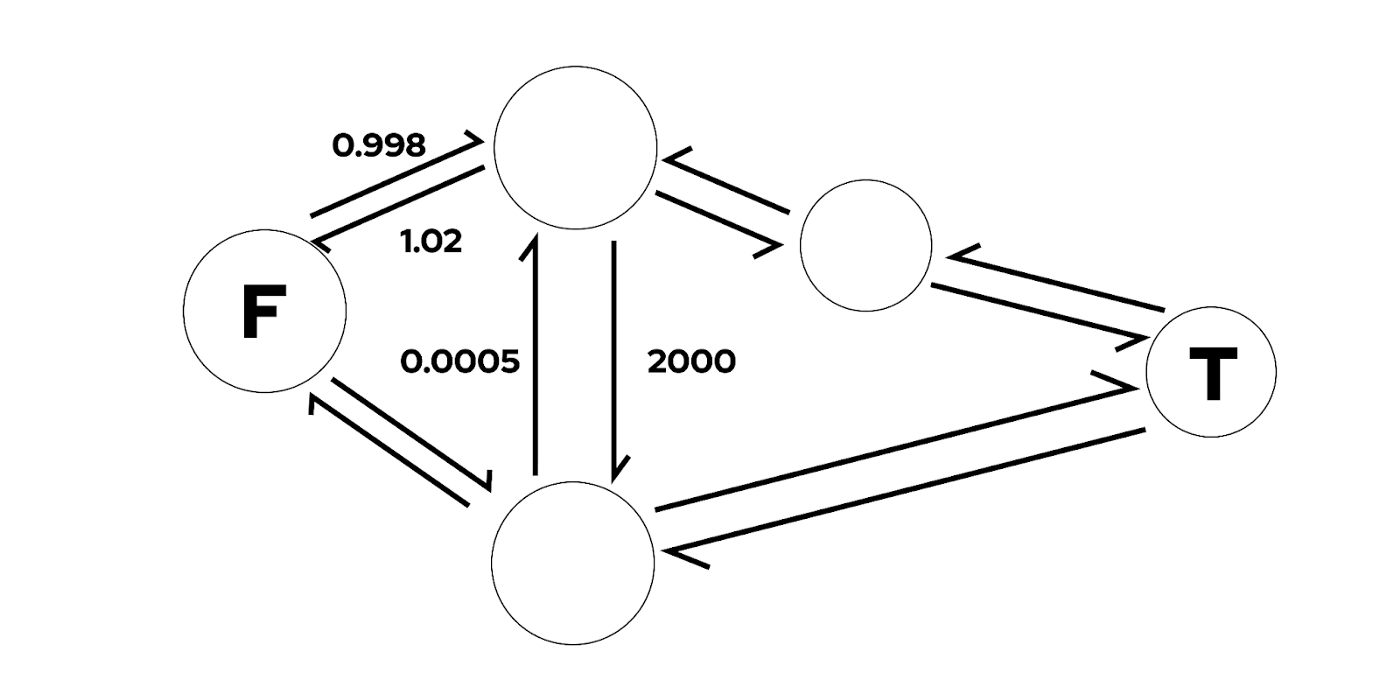
则可以将问题归结为,从原点 F,即 fromToken,寻找一条路径,使得到达 toToken 时,权重最小。
乍一看是一个非常简单的最短路问题,也有许多成熟的算法可供参考。但与普通的最短路问题不同的是,寻找下一条边时,下一条边的权重与节点的前序路径有关,因此,在进入队列优化路径时,节点是带状态的,必须实时维护每个节点的状态,使得后序节点所记录的路径长度与前序节点的状态匹配。且在该问题中,最后所求的“最小权重”,计算方法并不是将路径上的所有边的权重加和,而是仅计算 toToken 节点的入度权重。这个特性使得传统的最短路算法完全不适用。
当节点比较少时,比较直观的想法是直接采用 dfs 搜索,遍历每一条路径,得到最终 toToken 的价格,选取最优的一条路径为用户兑换。Uniswap V2 的 route 即采用该种方法寻找最优路径,第一版的 Uniswap V3 路由也是该方式,但与 V2 不同的是,V2 可以直接通过链下计算得到价格,V3 的价格是读合约数据计算所得,因此在 V3 的前端中,会先通过遍历找出所有的 path,再 multicall 调用 quoter 合约直接拿到计算结果。
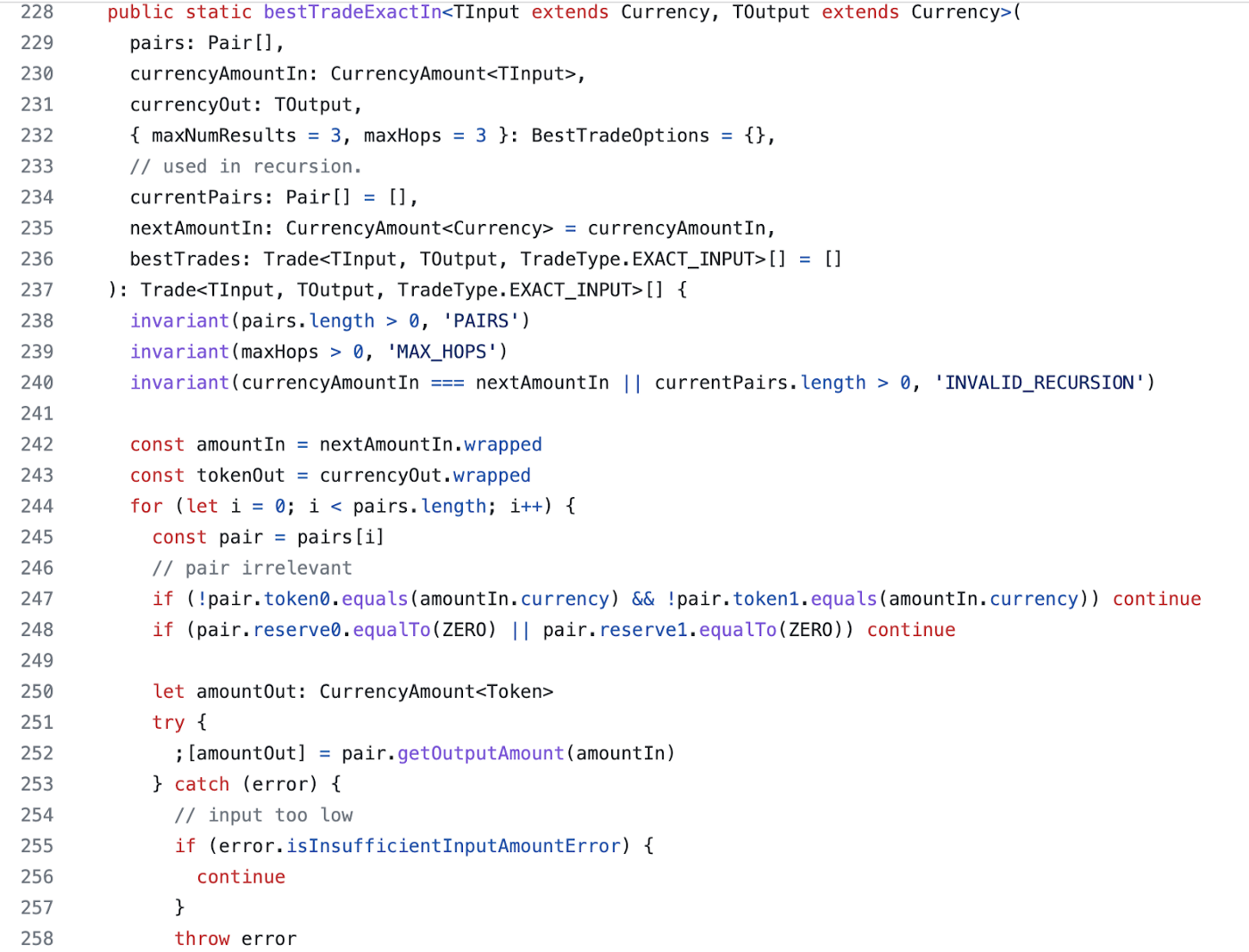

该模型不太适用于 BFS,如果按照边进行 BFS(即按照池子进行 BFS),需要同步维护该状态未选用的池子,下一步只能在未选用的池子中进行拓展,这样与dfs的复杂度没有区别,反而大大增大了记录所需的空间成本;而如果按照节点进行 BFS 拓展,则会遇到一个致命问题:因为此时节点是可以重复遍历的,不满足 BFS 条件。
同样由于有后效性,暂时没有想到在 DFS 中剪枝的规则,退而求其次的方法为对池子规模等做预处理排序,在进入 DFS 前删去一些池子,但删池子并不是全无风险的,可能对最优性造成影响。
应用 DFS 算法,一定能保证得到当前图从 fromToken 到 toToken 的最优路径,时间复杂度与层数有关,万幸的是,出于保证 gas 合理的考虑,递归层数不会超过 4,则时间复杂度为 O(l³), l 为总边数。
1.2 拆单路由
考虑复杂的问题,选取最优报价路径,又称拆单路由。寻找交易路径的过程中,一交易对可能经过不同的池子,用户的资金按最优比例配置到不同池子进行兑换,以使得目标token报价最优。同样以交易 ETH-USDC 为例,交易路径所经过的币种仍为 ETH-USDT-USDC,ETH 与 USDT 交易对可能经过两个池子,用户 30% 的 ETH 通过 Uniswap V3 兑换成 USDT,70% 的 ETH 通过 DODO V2 兑换成 USDT,进行下一交易对 USDT - USDC 兑换时,初始的 USDT 是以上两部分 USDT 所得的加和,再以此寻找 USDT-USDC 的最优拆分。
最优报价路径中可按照路径数额占比,将完整的 fromAmount 分成不同路径,或不同池子进行交易。按照划分时最小的比例单位不同,可以在原图中定义一个流网络。设 fromAmount 最大分为 n份,可建立一个超级源点,超级源点到 fromToken 节点的流量上限为n,剩余的边流量上限均为正无穷。a0 除以该池子换取的 quoteToken 数量 aj,α₀/αⱼ 作为边的费用 cⁱʲᵏ,运用如上所述的简化方法,k 池中仅包含 i,j 两种 token,可简化表示为 cʲᵏ。则问题转化为在该图中寻找最小费用最大流。
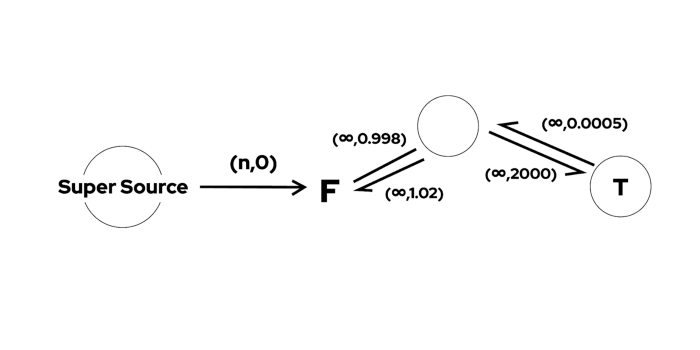
特殊的是,费用是动态的。具体而言,为了保持节点的出度和入度相等,我们可以认为在经过节点时,流不会增加或减少(均为原amount的x%),仅仅影响费用大小。因为边的费用和 baseToken 的 amount 有关,amount 又和路径有关。因此,每条边的费用 w 可定义为:
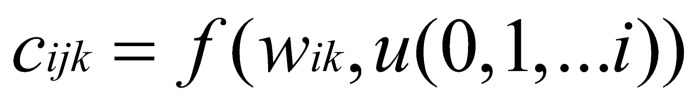
其中 cⁱʲᵏ 为,baseToken为 i,quoteToken为 j,池子编号为 k 的路径费用,是 wⁱᵏ 的函数,该函数即为池子的报价函数。u 为从 0 到 i 的路径。而 wⁱᵏ 定义为节点i中,会走k路径的流量。则有:
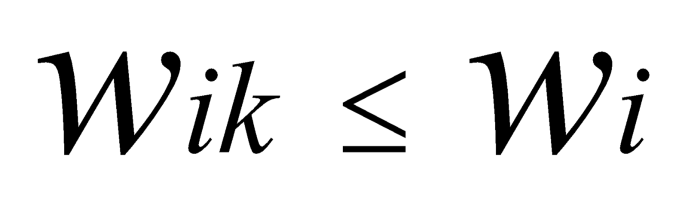
wⁱ 为 i 的节点流量。
又因为实际影响 quoteToken 数量的因素仅为 baseToken 的数量。可以进一步将 cⁱʲᵏ 简化为:
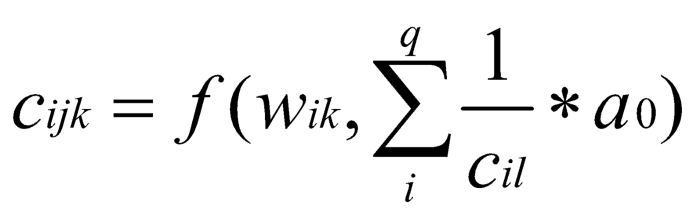
其中 cᵢₗ 为节点 i 的入度费用,ι∈ ∑ [1,…,q],q 为入度边数。
为了解决划分比例的问题,一种常见思路为,将可能的流量拆成 n 份,进而将 Pⁱʲᵏ 边拆成 n 份。流量等分 n 份,记为 wⁱᵏ=1,2…n, 其中要求:
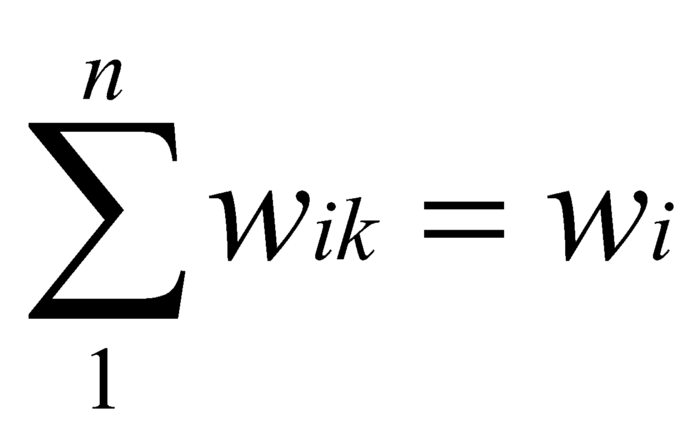
其对应边 P’ⁱʲᵏ,0<o<n+1,则 cⁱʲᵏ 定义为:
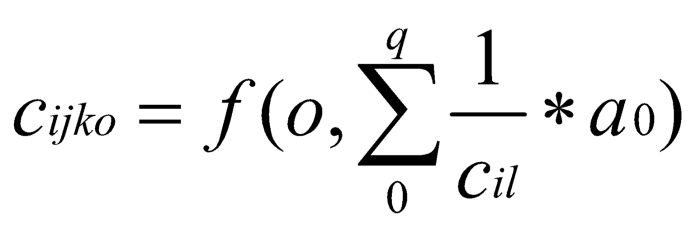
且要求同一组边拆分出的子路径不能重复选取。
同样的,问题最后所求解的最小费用仅由 toToken 的入度费用定义。
由于费用对过往路径的依赖,解决最小费用最大流的通常的增广路的算法无法适用。另一个问题是,这种拆边方法限制同一个池子只能走其中一条拆分子路径,子路径间不能加和计算,增广路也无法简单退流。
该问题需要另外的解决方法。因为该问题实际为一个求最值问题,当算力与时间足够时,可以考虑随机模拟参数,利用 MCMC 估计参数,暴力求解。实际在工业中,人们更在乎时间和可靠性,或许也不需要该原始问题的最优解。下文中,笔者试图分析业内其他聚合器的方案,以阐释两种简化问题的解法。
1.3 聚合器分析
0x
通过对 0x 源代码和 api 返回结果的分析,0x 实际将问题简化为两个独立模型,各自给出最优报价,再选择最优解返回给用户。
简化问题1:线性路由,即 api 返回中的 multiHops 结果。
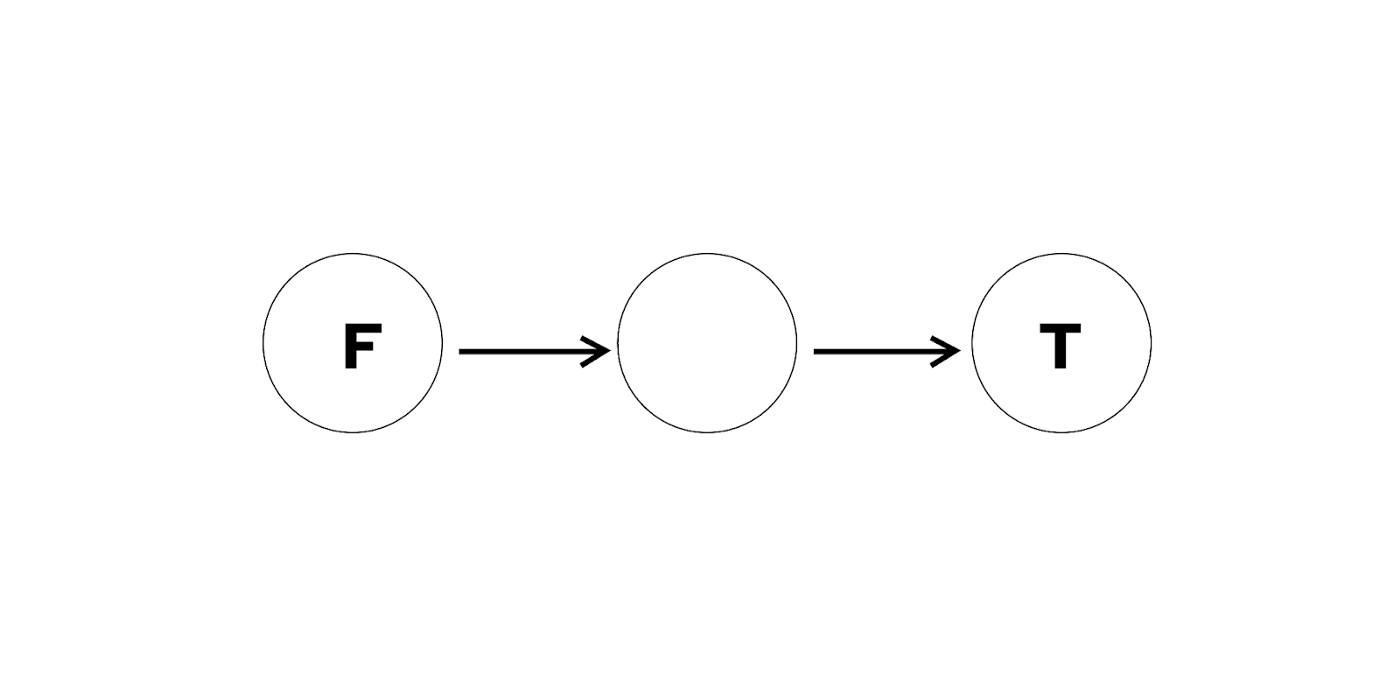
简化问题2:单跳的拆单路由。仅保留 fromToken 到 toToken 的池子。
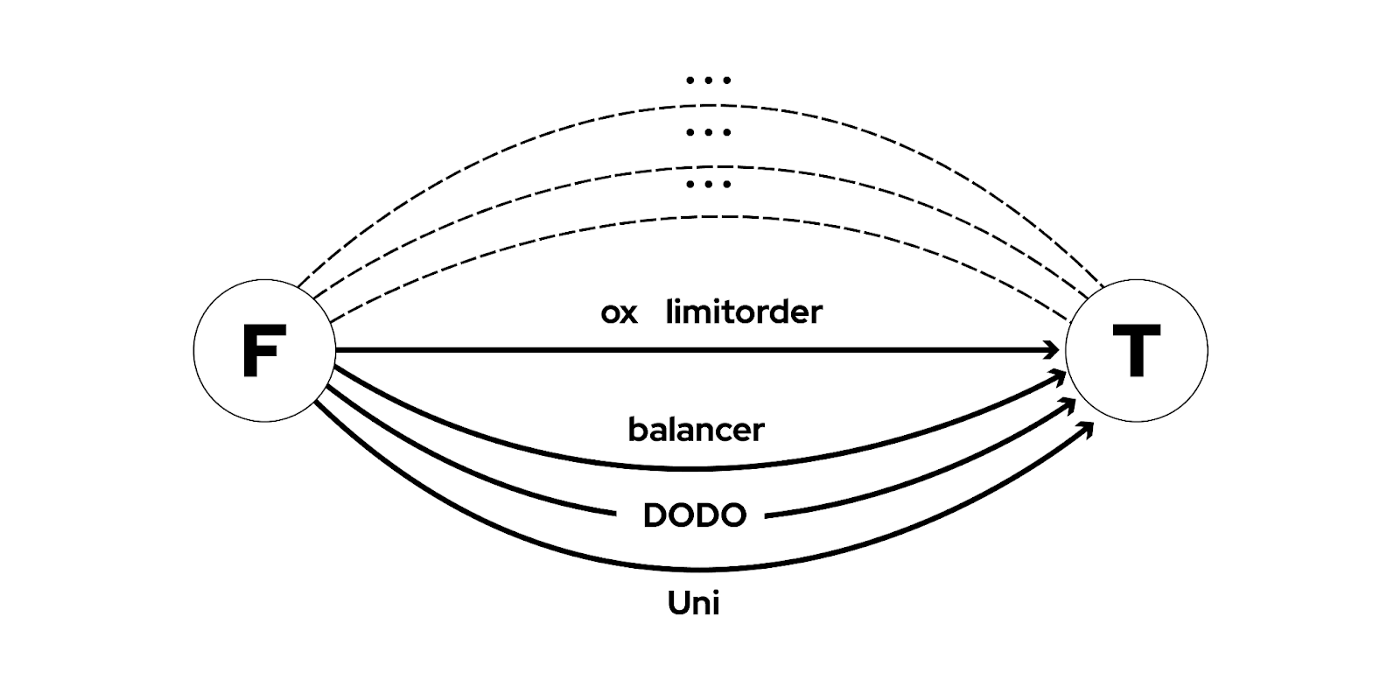
对于单跳的拆单路由,可以将每条路径按照离散系数 n 拆成 n 条子路径,每条子路径的费用为流量为i时的 quoteToken,也是 toToken 的单位价格,而后求解。
特殊地,0x 在构造 sushiSwap 或 Uniswap 相关的路径时,调用的 route 合约询价,因此该路径中可能会有多个中间跳币种,实质上是将这跳看为一个完整池子进行计算。
1inch/ParaSwap
对于1inch,1inch V2 中的 gas 最优路径即为线性路由。
1inch V2 的拆单路由更新了 pathfinder 算法,该 pathfinder 的结构如下:
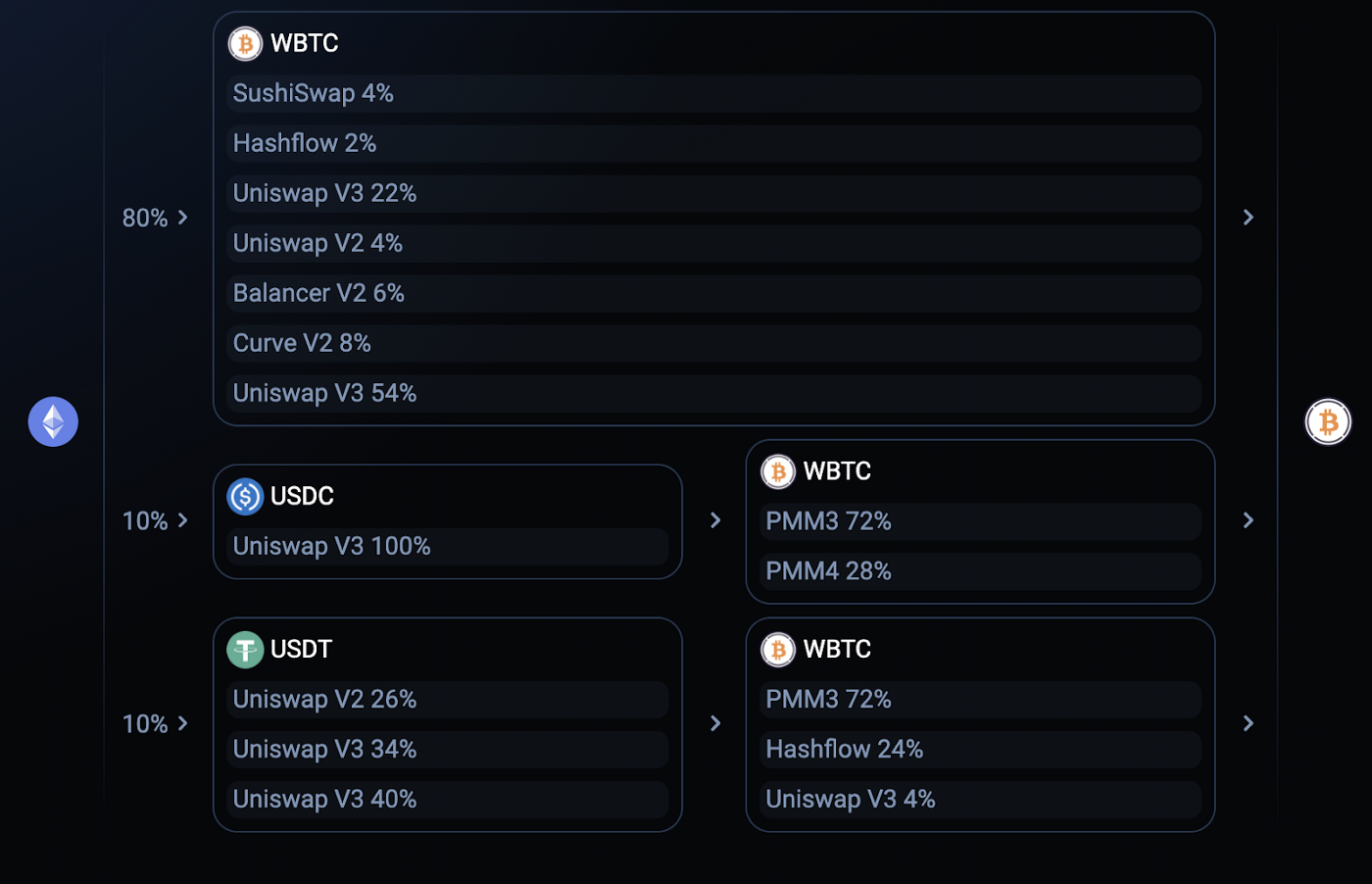
无独有偶,ParaSwap 采用了和 1inch 一样的模型:

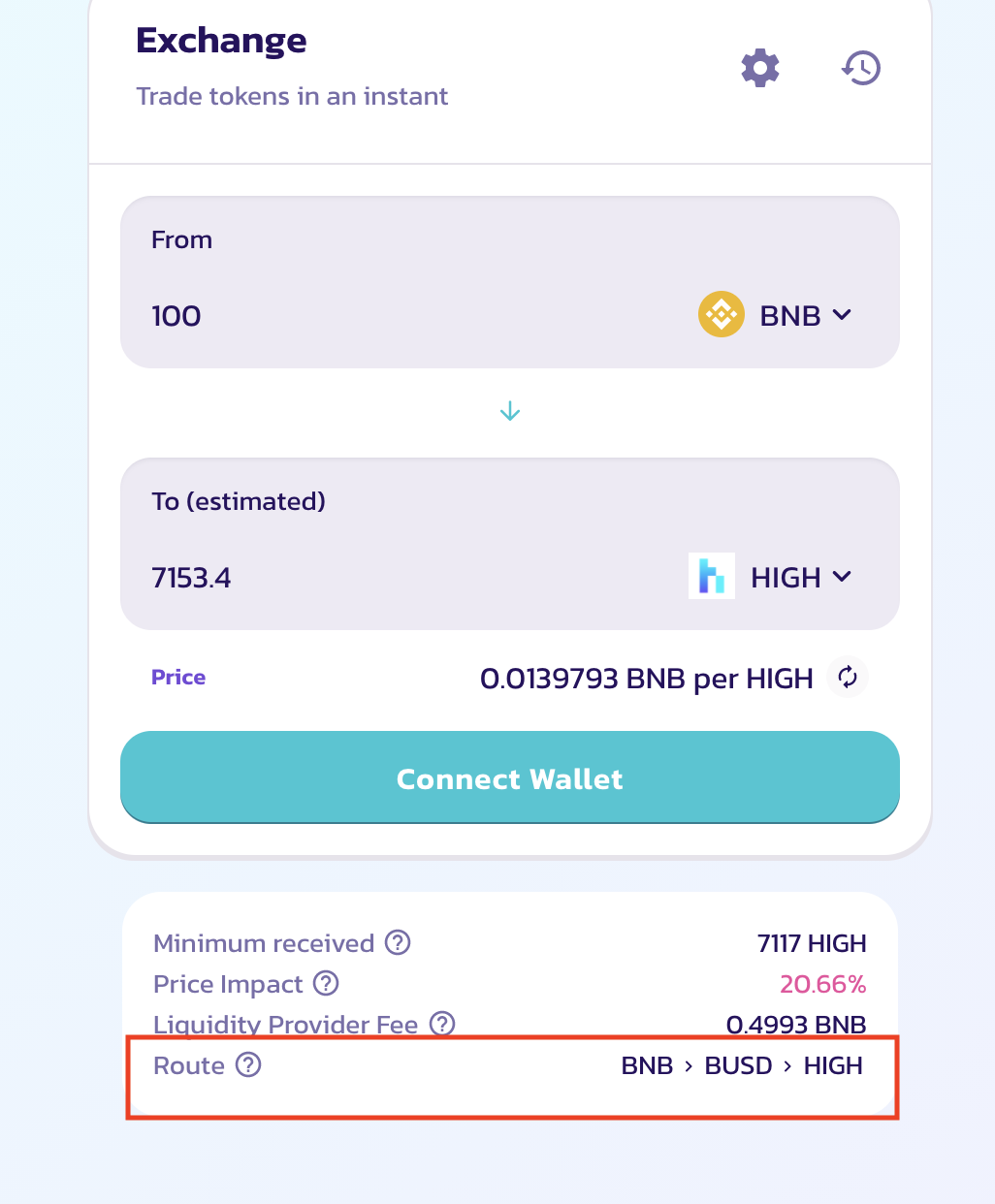
前端并没有展示单跳中的拆分路径,但 api 中可以观察到拆分结果:
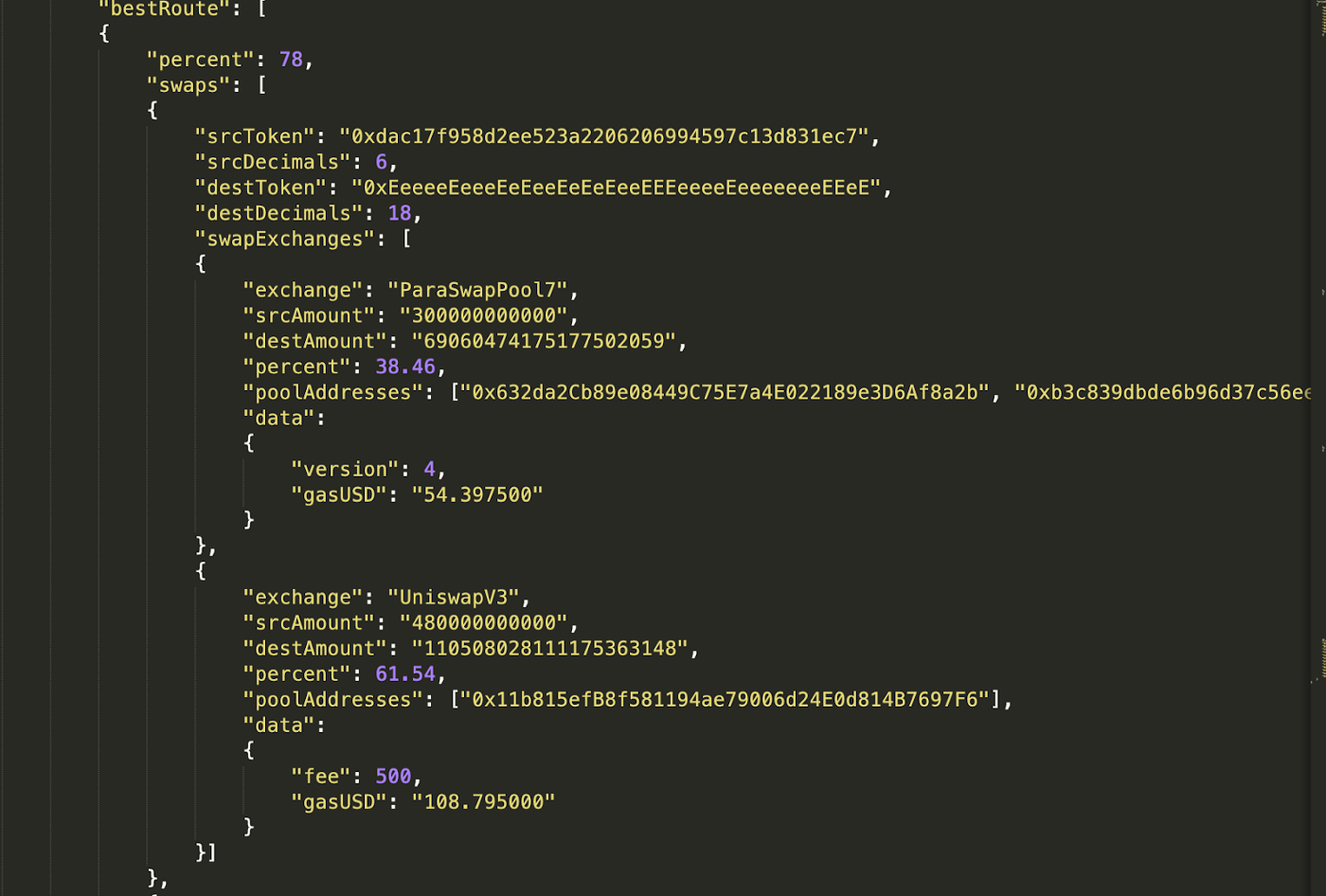
[api中bestRoute 字段记录了路由路径的细节,如图可以看出,在 usdt(0xdAC17F958D2ee523a2206206994597C13D831ec7)-eth 对中,ParaSwap 选择了ParaSwapPool7 (占比38.46%)和 Uniswap V3(占比61.54%)两个池子进行交易]
该模型直接可表示为:
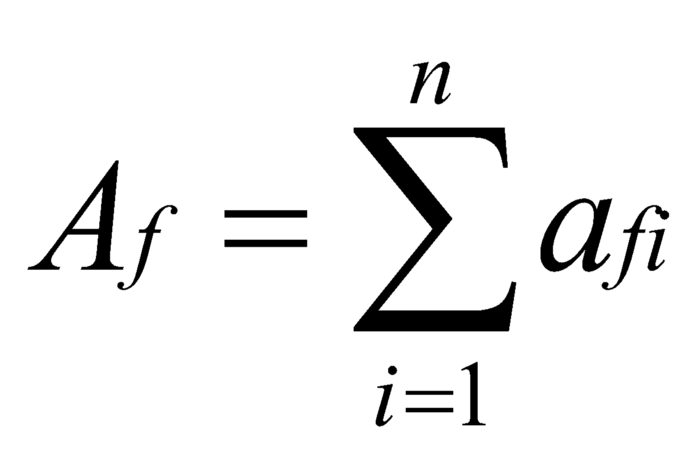
其中 Af 为 base token 总额,拆分成 n 条路径分别交易。记最终所获得的 toToken 数量为 At, At 同样为 n 条路径之和。
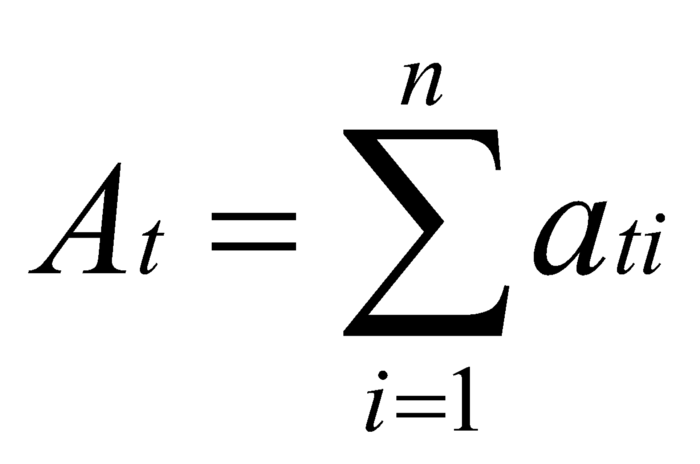
对于每一条路径,可能会经历数量不等的池子/交易所,中途交换不同的代币,利用上文中的模型,可以直接将 ati 表示为:
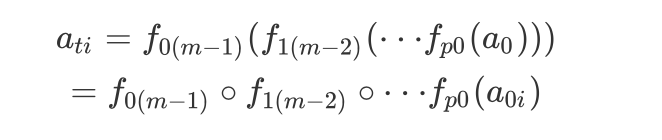
该解法可以理解为在问题中找出三条互不重复的费用最小路径,比 0x 的算法更加接近最优解。但它同样是一个简化版本,考虑一种隐蔽的情况,两条不同路径汇流到同一个节点。
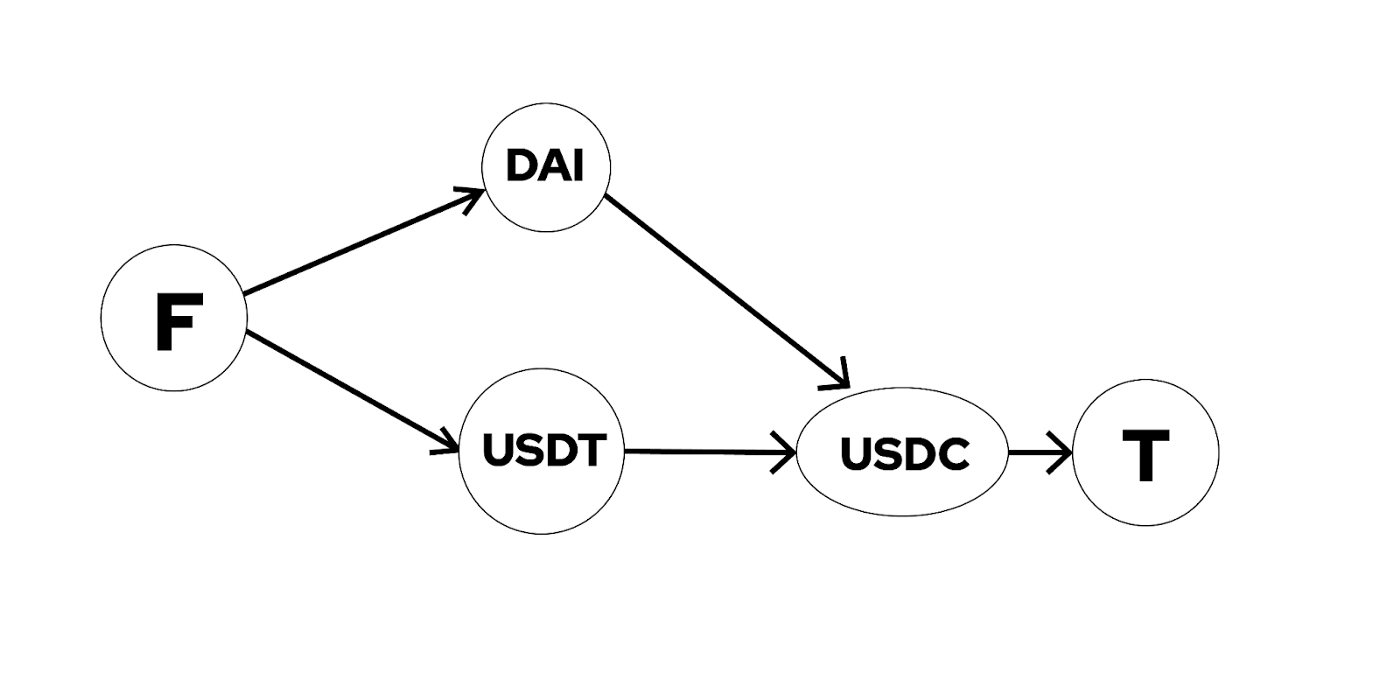
尽管 1inch 的 pathfinder 在设计子 token 路径时没有排除重复节点(即不同路径经过相同币种),1inch 为不同的子路径分配了不同的报价源,避免了同一报价源使用两次的问题,但在一些情况下,它的解仍会和最优解有差距,具体的影响大小可以进行敏感度测试。
但如分析所示,该模型最接近原始模型,如能对该问题给出最优解,则该解更接近原问题给出了最优解(可以测算模型扰动)。唯一的影响为,观察 1inch 的 api 参数和结果,可以推测 1inch 对amount 进行了指定份数的离散处理,**可能会造成一些离散误差。**观察 ParaSwap的拆分比例,似乎比 1inch 颗粒度更细,在一些情况下,ParaSwap能得到比 1inch 更好的结果,或许这是一个影响因素。
DODO
DODO 自建路由算法参考 1inch 和 0x 的设计,也对问题进行了简化处理。在路由 V1 版本中,考虑到 gas 消耗和交易成功率我们将其简化成了如下模型:
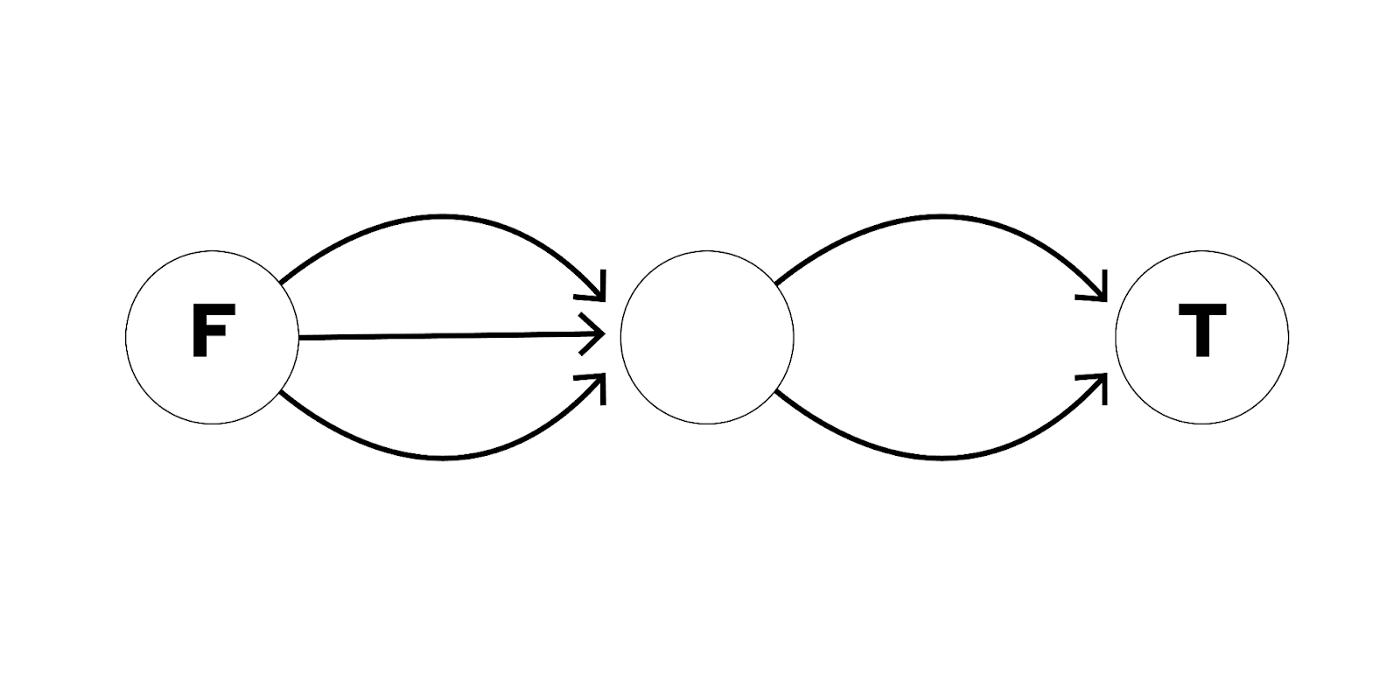
即 token 路径唯一,池子路径不唯一。
在路由 V2 版本中,DODO 将参考 1inch 和 ParaSwap 的模型设计,优化成多 token 路径,多池子路径的拆单路由。
本篇分享了聚合器问题的几种可能的建模方式,在下篇中,我们将依据 DODO 的自建路由算法给出一种可能的工程设计思路。