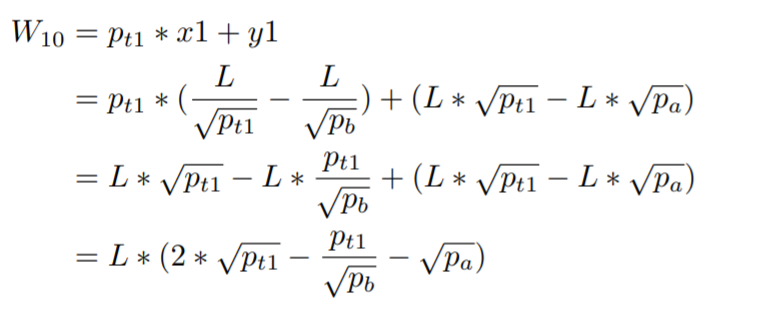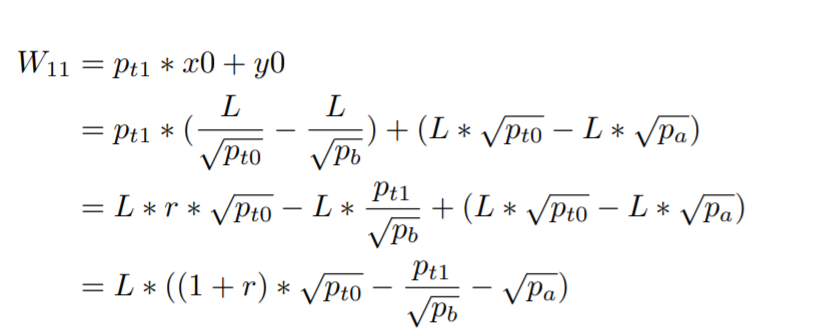Uniswap v1
- Constant Product Market Maker
- ETH/ERC20, ETH bridge currency
任意两个数量的资产价格只取决于数量(quantities)本身,而不取决于它们之间的路径。这提供了两个重要的好处: (path dependence vs. path independence)
- 由于交易者在单次交易中获得的价格与在一组小量交易中获得的价格相同,交易者不需要为其制定交易策略
- 它尽可能地给出了一项资产的状态:我们只需要知道资产的数量就可以为其定价
Uniswap v2
- Arbitrary ERC20/ERC20
- price oracle ==> keep track of the cumulative sum of prices at the beginning of each block in which someone interacts with the contract. ==> time-weighted average price
- track price a/b and b/a at the same time
- Impermanent loss calculator
Understanding math
x, y represent the quantity of token x and y.
x * y = k = L^2
how to get the Price of token x denominated in token y
y = L^2 / x
dy = - L^2 / x^2 dx
==>
P = - dy / dx = - (- L^2 / x^2 dx) / dx = L^2 / x^2 = y / x
==>
x = L / sqrt(P)
y = L * sqrt(P)

Impermanent Loss
w10: wealth at time t1 if participate as UNISWAP LP at time t0
w11: wealth at time t1 if hold half asset x and half asset y at time t0
p(t1): price for x at time t1
p(t0): price for x at
time t0
!!! all the wealth are denominated in y.
w10 = p(t1) * x1 + y1
= p(t1) * L / sqrt(p(t1)) + y1
= L * sqrt(p(t1)) + y1
= 2 * L * sqrt(p(t1))
Assume r = p(t1) / p(t0)
w11 = p(t1) * x0 + y0 【the quantities remain the same】
= p(t1) * L / sqrt(p(t0)) + y0
= r * P(t0) * L / sqrt(p(t0)) + y0
= r * sqrt(p(t0)) * L + sqrt(p(t0)) * L
= (1 + r) * sqrt(p(t0)) * L
IL = w10 / w11 - 1
= 2 * L * sqrt(p(t1)) / ((1 + r) * sqrt(p(t0)) * L) - 1
= 2 * sqrt(p(t1)) / ((1 + r) * sqrt(p(t0))) - 1
= 2 * sqrt(r) / (1 + r) - 1
If we only care about the initial investment in the value of y,
w00: wealth at time t0 (in token y)
w12: wealth at time t1 if hold all asset y at time t0
w12 = w00
= p(t0) * x0 + y0
= p(t0) * L / sqrt(P(t0)) + L * sqrt(P(t0))
= 2 * L * sqrt(p(t0))
Assume r = p(t1) / p(t0)
IL = w10 / w12 - 1
= 2 * L * sqrt(p(t1)) / (2 * L * sqrt(p(t0))) - 1
= sqrt(p(t1)/p(t0))- 1
= sqrt(r) - 1
If we only care about the initial investment in the value of x,
w13: wealth at time t1 if hold all asset x at time t0
w13 = p(t1) * (2 * x0) [hold 2*x0 all time]
= 2 * p(t1) * L / sqrt(P(t0))
= 2 * r * P(t0) * L / sqrt(P(t0))
= 2 * L * r * sqrt(P(t0))
IL = w10 / w13 - 1
= 2 * L * sqrt(p(t1)) / (2 * L * r * sqrt(p(t0))) - 1
= sqrt(r) / r - 1
= 1 / sqrt(r) - 1

If we only care about the initial investment in the value of y, and we participate the pool and hedge x0 at time t0【we don’t consider the hedging fees here】
w00: wealth at time t0 (in token y)
w12: wealth at time t1 if hold all asset y at time t0
k: hedge ratio in terms of x0
w14: wealth at time t1 if participate pool and hedge k * x0 at time t0


Conclusion
The loss varies depending on how investors think of their initial deposit. For example, x=BTC, y=USDT, investors who originally hold all their position in BTC and think of possible downtrend may provide liquidity in this case and actually benefit from the decline of BTC price compared to simply holding all BTC. But still, the liquidity provider has some exposure to the upside compared to converting all BTC to USDT. Meantime, the LP generates profit from transactions.
For investors who seek only capital gains in USDT (y here), becoming liquidity providers could be beneficial, as long as they employ some hedge.
Uniswap v3
- concentrated liquidity ==> increased capital efficiency
- smaller range ==> higher fees
- range order ==> limit order
- in range ==> fees; not in range ==> no fees
If the current price = Pc, we have x quantity of asset X and y quantity of asset Y in the pool.
In v2, if the price moves between Pa and Pb, only x_real and y_real are utilized. The quantity (x- x_real) and (y - y_real) are never touch. Given that in mind, we only need to keep x_real and y_real in that pool to provide the same amount of liquidity instead of having x and y (larger than x_real and y_real).

In the graph below, the green line and the orange line have the same liquidity, but the green line need x, y, the orange line only needs x_real and y_real. Why we put x and y if we only need x_real and y_real?

what's new:
Pa: low range for x
Pb: up range for x
Pc: current price for x
Pa < Pc < Pb
x_v: virtual reserve for x
y_v: virtual reserve for y
L: virtual liquidity
(x + L / sqrt(Pb)) * (y + L * sqrt(Pa)) = L^2
x_v * y_v = L^2
x_v = x + L / sqrt(Pb)
y_v = y + L * sqrt(Pa)
x = x_v - L / sqrt(Pb)
= L / sqrt(Pc) - L / sqrt(Pb)
y = y_v - L * sqrt(Pa)
= L * sqrt(Pc) - L * sqrt(Pa)
Impermanent Loss
w10: wealth at time t1 if participate as UNISWAP LP at time t0
w11: wealth at time t1 if hold half asset x and half asset y at time t0
Assume r = p(x1) / p(x0)