We are developing a new yield-bearing stablecoin which has not been explored by many yet. As a result, explaining the mechanism behind our model is crucial.
Stable Jack partitions AVAX volatility into two products to have a new yield-bearing stablecoin, called aUSD, while also creating a volatile AVAX token, called xAVAX.
To make things simpler, we should consider the entire system as one big CDP in which:
-
the total AVAX reserve represents the total CDP collateral
-
the total aUSD supply represents the borrowed amount
-
the xAVAX supply represents the difference between supplied collateral and the total borrowed amount
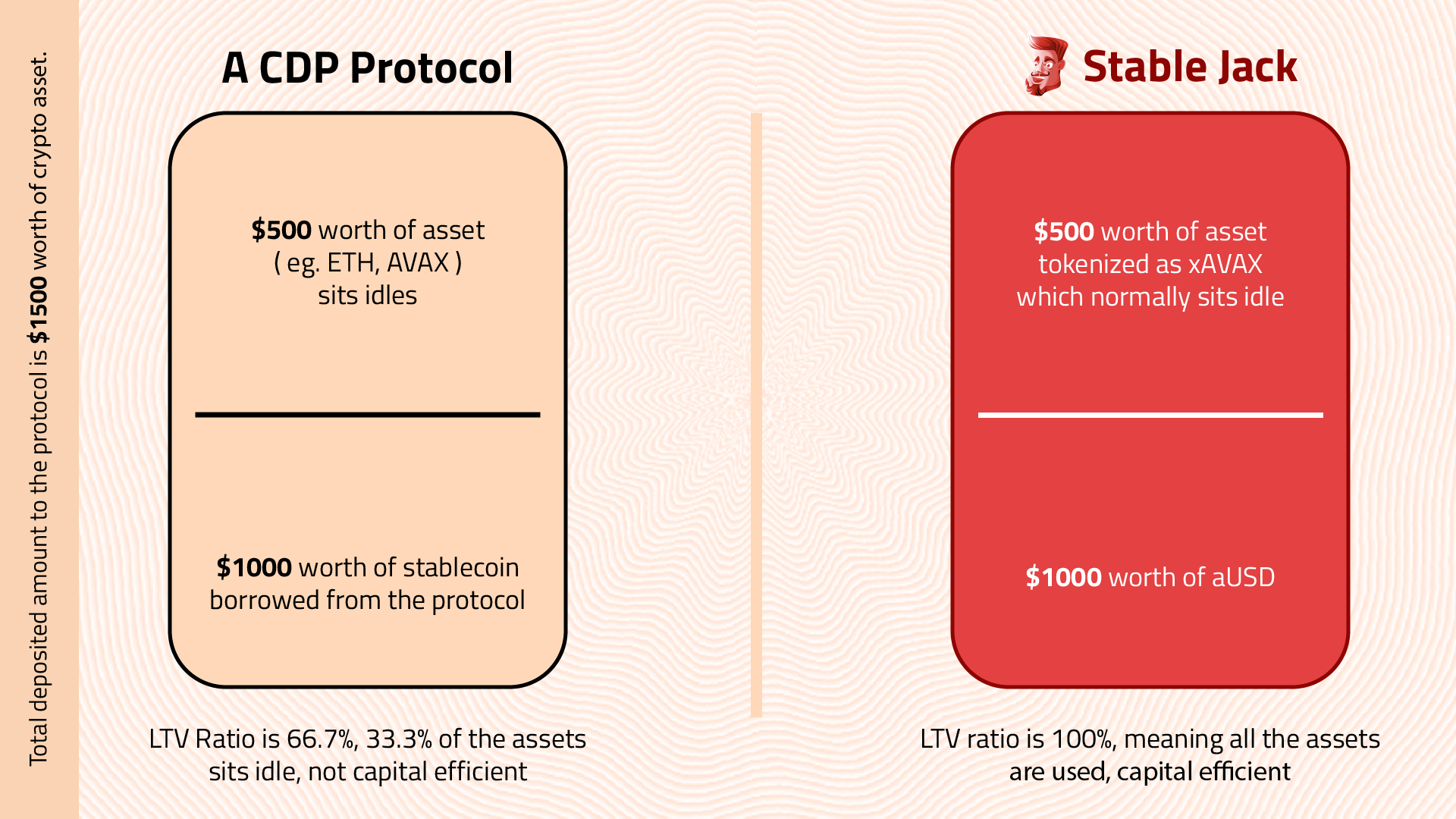
As a result, the total value of all aUSD and xAVAX tokens equals the overall AVAX LST reserve value. This connection is expressed through the equation:
The quantity of AVAX LST Collateral × AVAX LST Price in USD = (Total Supply of aUSD × NAV of aUSD) + (Total Supply of xAVAX × NAV of xAVAX).

Here, the Net Asset Value (NAV) represents the current mint/redemption value of aUSD or xAVAX as determined by the protocol. The protocol maintains the stability of aUSD by consistently valuing it at $1, reflecting a fixed ratio of Δ=0 of AVAX's price. Simultaneously, it adjusts the NAV of xAVAX more significantly than the AVAX return to uphold this invariant.
This strategy enables xAVAX to provide leveraged AVAX returns without incurring funding costs, while aUSD retains its peg to $1.
In other words, total AVAX LST collateral value in the protocol = Total market cap of aUSD + Total market cap of xAVAX
Example 1
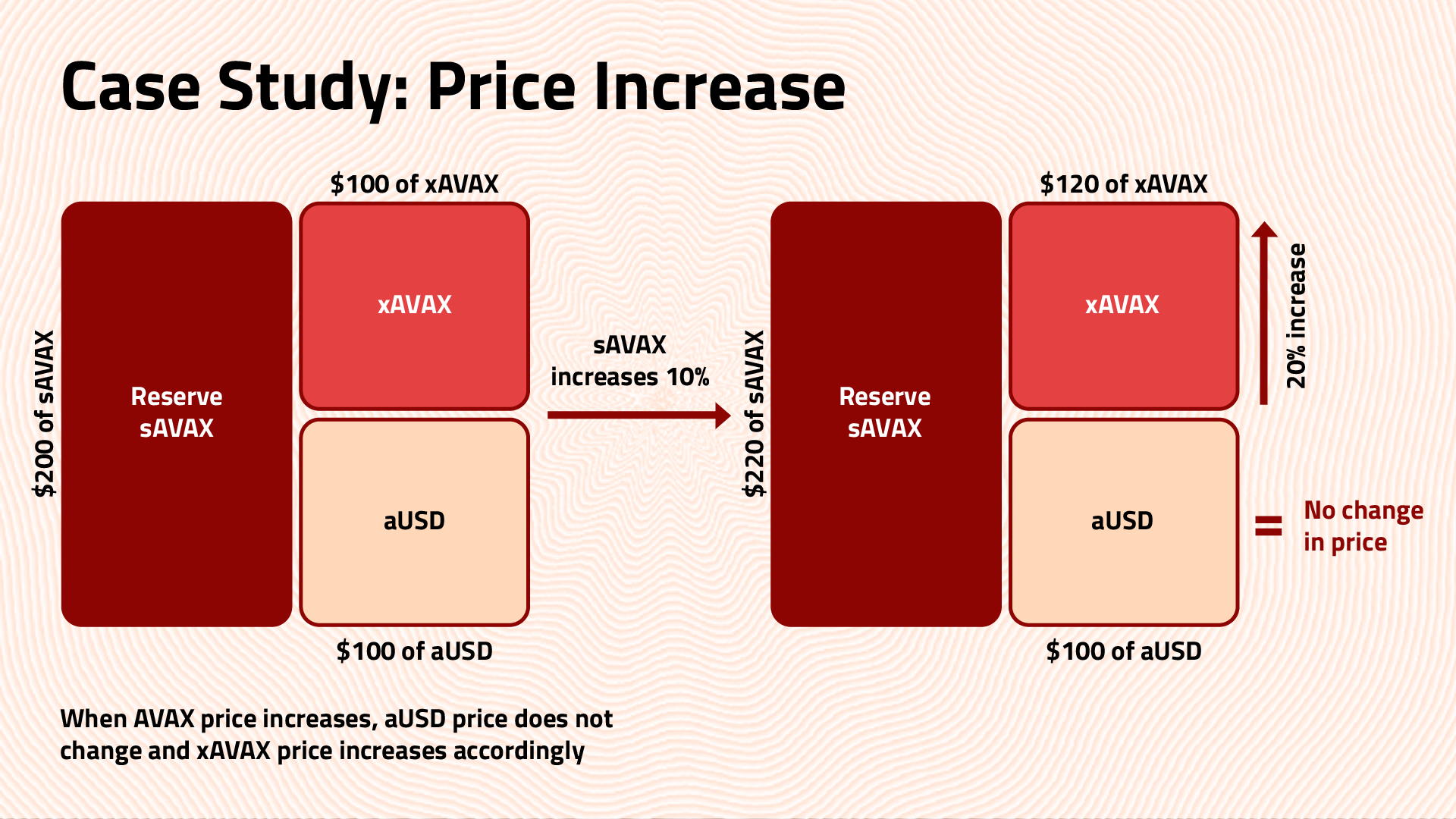
User A deposits $100 worth of AVAX and mints 100 aUSD
User B deposits $100 worth of AVAX and mints 100 xAVAX
Total Pool: $200 worth of AVAX
AVAX price increases by 10%
New Total Pool: $220 worth of AVAX
-
aUSD Worth: $1 (no price exposure)
-
xAVAX Worth: $1.2 (all price exposure)
User A redeems 100 aUSD and receives $100 worth of AVAX User B redeems 100 xAVAX and receives $120 worth of AVAX
Note 1: The price of xAVAX is initially $1, subject to change based on AVAX price action. Note 2: Even though the price of AVAX increased by 10%, aUSD has no price exposure (Δ=0), while xAVAX increased by 20% (Δ>1).
Note 3: Collateralization ratio is assumed %200, meaning that xAVAX leverage is 2x.
Example 2
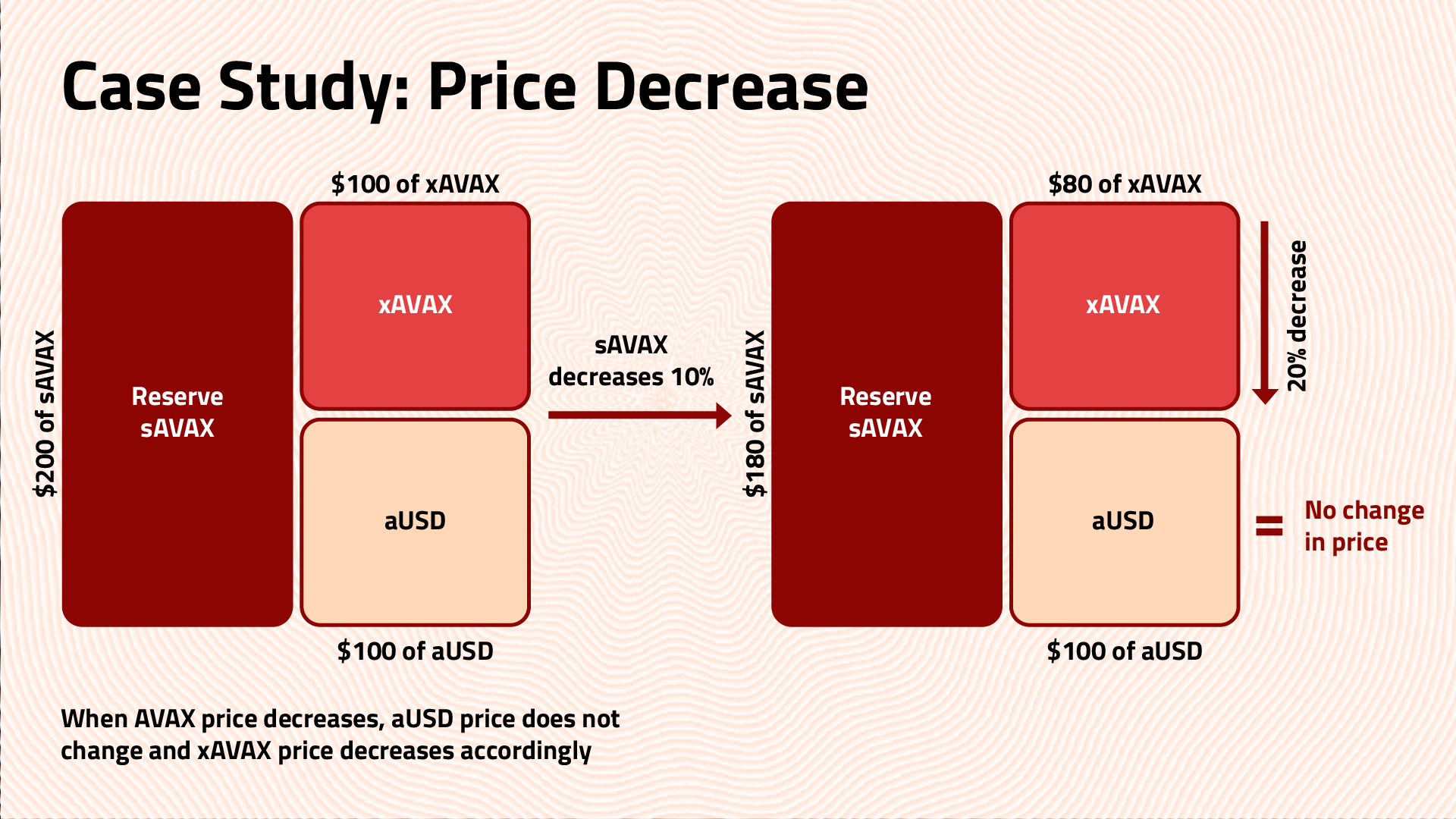
User A deposits $100 worth of AVAX and mints 100 aUSD
User B deposits $100 worth of AVAX and mints 100 xAVAX
Total Pool: $200 worth of AVAX
AVAX price decreases by 10%
New Total Pool: $180 worth of AVAX
-
aUSD Worth: $1 (no price exposure)
-
xAVAX Worth: $0.8 (all price exposure)
User A redeems 100 aUSD and receives $100 worth of AVAX User B redeems 100 xAVAX and receives $80 worth of AVAX
Note 1: The price of xAVAX is taken as 1$ because, at the genesis of the protocol, the price of xAVAX will be $1, but then it will change based on the AVAX price action.
Note 2: Even though the price of AVAX decreased by 10%, aUSD has no price exposure as its Δ=0 while xAVAX has decreased by 20% as its Δ>1.
Note 3: Collateralization ratio is assumed %200, meaning that xAVAX leverage is 2x.
How to Determine xAVAX Leverage?
xAVAX’s precise Δ at any given time is based on the total relative supplies of aUSD and xAVAX, which are always changing.
i.e. when xAVAX’s Δ = 2, a 10% AVAX price increase would lead to a 20% increase in the NAV of xAVAX.
A higher supply of xAVAX relative to aUSD --> lower effective leverage as volatility is absorbed over more xAVAX tokens.
Conversely, a larger supply of aUSD concentrates volatility on fewer xAVAX tokens --> higher effective leverage.
Here's a detailed calculation that shows the xAVAX leverage in different scenarios:
What is the relationship between aUSD and xAVAX?
-
For the price stability of aUSD, there needs to be a sufficient supply of xAVAX as it acts as a barrier to maintain the collateral value of aUSD.
-
xAVAX is working as an insurance to aUSD, in which xAVAX carries all the volatility, in return for taking this risk, leveraged AVAX can return higher profits without any funding fee and unlikely liquidation risk
-
As the supply of aUSD increases, the supply of xAVAX should also increase to match the volatility risk of the collateral so that volatility can be distributed to xAVAXs. Similar to CDP models, if the borrowed amount increases, the supplied collateral should increase too so that the liquidation risk can be minimized.
-
If the supply of xAVAX increases, the aUSD supply can increases further.
-------------------
That’s all the necessary information you need to have about the Stable Jack protocol mechanism. However, if you have any questions, you can check our Gitbook or ask your question on the Discord channel!