Authors

Kishori Konwar (Optimum), Muriel Médard (Optimum/MIT), Nicolas Nicolaou (Optimum)

Abstract

Sending data over shaky or delayed connections often means it gets lost or delayed. The old way to deal with this was simply to resend anything that didn’t make it (like the TCP protocol does). But this approach has problems, especially on crowded networks where resending things just adds to the traffic jam and leads to further delays.

Erasure codes offer a different solution. They work by adding extra, often called redundant, information to help recover lost or damaged data. Basically, you break the original data into smaller pieces, then create some extra “coded” pieces using a special process. When you send these coded pieces (or shards), the receiver only needs to get some of them – not necessarily all – to rebuild the original data. This tolerance for missing pieces makes erasure codes great for unreliable situations like wireless networks, dynamic systems, and streaming applications.

With the rapid expansion of Web3 applications it is critical to answer the question: Which type of erasure codes are suitable for Web3 networks?

Random Linear Network Codes (RLNC) made their appearance in the early 2000s as an erasure coding solution for decentralized, highly dynamic environments such as the ones assumed in Web3 applications. Here, we argue that RLNC is a highly suitable candidate for Web3 network communication, outperforming conventional families of erasure codes, namely block erasure codes (e.g., Reed-Solomon codes) and fountain codes (e.g., Raptor codes).

1. Coding

When you send data over connections that aren’t reliable or tend to lose information, that data can get corrupted, mixed up, or just lost entirely. The usual way to deal with lost messages was just to send them again (like the TCP protocol often does). But this method had its problems, especially on crowded networks where sending things over and over could just make the congestion worse.

Erasure codes try to get around these issues. They use techniques that add extra, redundant information, which helps recover data that gets lost or damaged. How it works is, you divide the original data into smaller pieces (fragments). Then, you create some extra coded packets using a special process on those original pieces. When you send these coded pieces (sometimes called shards), the receiver doesn’t need to get all of them. They only need to receive a certain number of the pieces to figure out what the original data was. This makes the whole process tolerant to missing data. Because of this ability to handle lost pieces, erasure codes are really useful for tricky situations like wireless networks, systems spread across many computers that might change unexpectedly, and for streaming data smoothly.

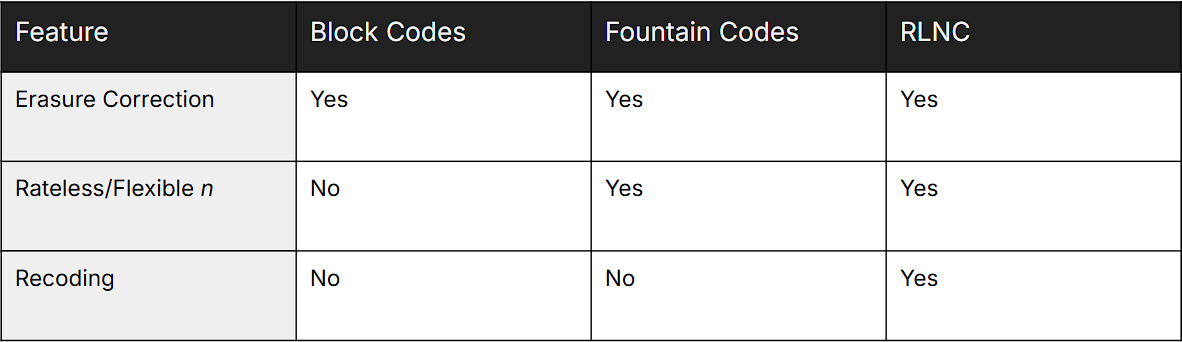
Three of the commonly used types of erasure codes are block erasure codes (e.g., Reed-Solomon [RS60]), fountain codes (e.g., LT codes [Lub02], Raptor codes [Sho06]), and network codes (e.g, Algebraic Network Codes [KM03], Random Linear Network Codes [HMK+06]) each offering trade-offs between complexity, overhead, and adaptability.

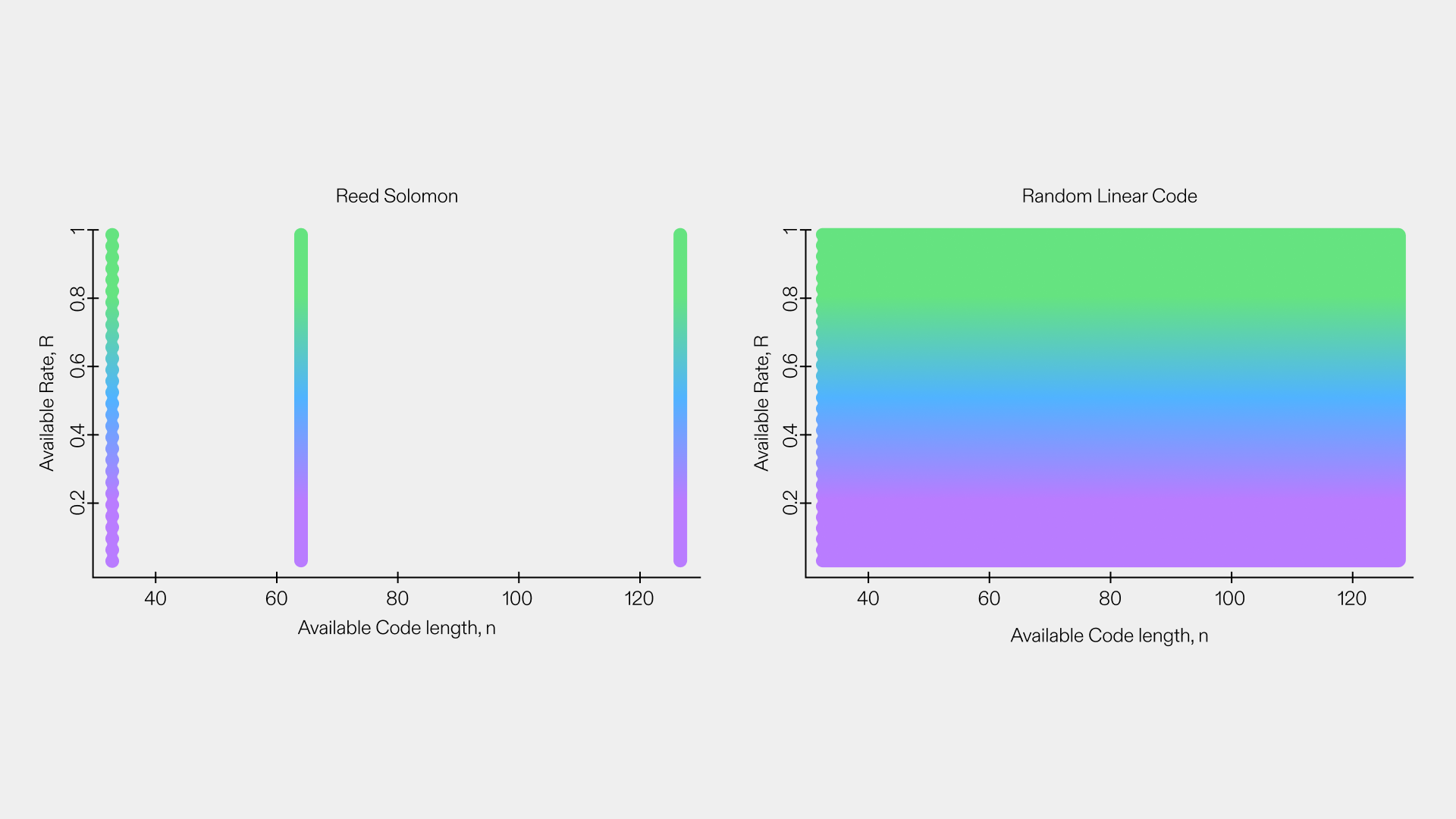
Block-based codes like Reed-Solomon (RS) [RS60] and many others presented in [LJ04], are a foundational class codes that work by transforming data into a polynomial representation and adding systematic redundancy. They have traditionally been designed as error correcting codes but then repurposed for handling erasures. A (n, k) RS code works by splitting the data into k pieces and generating n − k additional coded packets, each of similar size to the un-encoded k pieces, creating a total of n shards. Any k out of n shards can be used to decode the original value, placing RS in the category of Maximum Distance Separable (MDS) codes. The ratio of the initial fragments k, over the total number of shards n, i.e. $k/n$, defines the coding rate, which is used to specify the number of erasures RS codes may tolerate. RS codes are widely used in storage systems like RAID arrays, optical media (CDs/DVDs), and QR codes owing to the fact that they are well understood. In network environments, RS codes as single source encoding mechanisms, meaning that coding is happening only at the source and decoding may happen at the targets.

Fountain codes, including LT [Lub02] and Raptor codes [Sho06], are rateless erasure codes, i.e. without predefined redundancy as in RS, designed for environments where loss rates are unpredictable. Unlike block codes, Fountain codes generate an unlimited stream of encoded packets, each constructed by combining original data shreds. The receiver can reconstruct the original data once it collects enough unique packets, eliminating the need for precise coordination between the sender and the receiver. This makes fountain codes suitable for one-to-many communication scenarios, such as multimedia streaming (e.g., DVB-H, IPTV), where the losses to different receivers may be different. Variants like Raptor codes [Sho06] reduce decoding overhead by preprocessing data.

Algebraic Network Coding (NC), represents a paradigm shift by allowing intermediate network nodes to combine (and not just forward) coded packets algebraically. The existence of NC was first discussed by Ahlswede, Cai, Li and Yeung in 2000 [ACLY00]. To be able to map network coding to actual coding Kötter and Médard [KM03] presented an algebraic framework for NC by representing the processes in each network node as algebraic equations and in turn the network response in the form of a matrix. They showed how matrix manipulations may allow both encoding and decoding of data. Decoding involves solving a system of linear equations once enough independent combinations are received. Random Linear Network Codes (RLNC) [HMK+06], further enhanced the applicability of the NC of [KM03] by allowing the selection of random coefficients in the generated equations, and hence, the generation of random linear combinations of original shards at each network node, which we refer to as recoding. In contrast to deterministic network coding, RLNC does not depend on any deterministic rules or predefined structures. This characteristic provides RLNC the ability to be superior over other approaches in decentralized and dynamic environments, such as wireless mesh networks, IoT systems, and 5G communications, where traditional codes struggle with fluctuating topology or intermittent connectivity. Furthermore, its ability to exploit path diversity and reduce redundant transmissions makes it uniquely suited for multicast and multi-hop scenarios [MAVPD25].

It is important to point out that RS codes are never better than RLNC. They are simply a degenerate, needlessly constrained version of a random code. That constraint arises from the fact that they were developed over half a century ago, for a different purpose. As seen in Figure 1 RS (left plot) simply poses unnecessary and often highly detrimental constraints (figure courtesy of Ken Duffy).

Table 1: Key Characteristics of RLNC, Reed-Solomon, and Fountain Codes

2. Let the Network Grow: The Power of Recoding

So, what’s the big deal with recoding? Well, let’s dive into how things work. Picture this: we’re sending data through a network, but it’s not always perfect. Sometimes, the network connections (the channels) drop packets, and that’s where erasure coding comes to the rescue. Imagine, for example, that every lossy channel drops 1 every 10 messages it transfers.

Now, let’s start with a simple setup: a single point-to-point connection. In this case, the source sends the data directly to the receiver. Using any coding technique the source would do the following: encodes the data, by adding some extra shards to make up for the lost packets, and then sends the shards to the receiver. In our example, if the receiver needs 10 shards to decode the value then the source will prepare 11 shards. So, the receiver gets enough shards to decode the original message, despite any losses from the network, and the delivery of the data to the receiver works at its best.

But what happens when we want to send data to multiple receivers at once? In such scenarios block codes fall short and fail to deliver. When block codes are used in a single-hop multicast setup, the source encodes the data based on specific coding parameter (n, k), and it divides the data into shards to be distributed to the receivers. Each receiver needs at least k shards to decode the original data. If some receivers will fail to collect k shards, they fail to decode the original data.

On the other hand, fountain codes and RLNC allow generation of coded packets indefinitely, which allow them to cope with different erasures at different receivers.

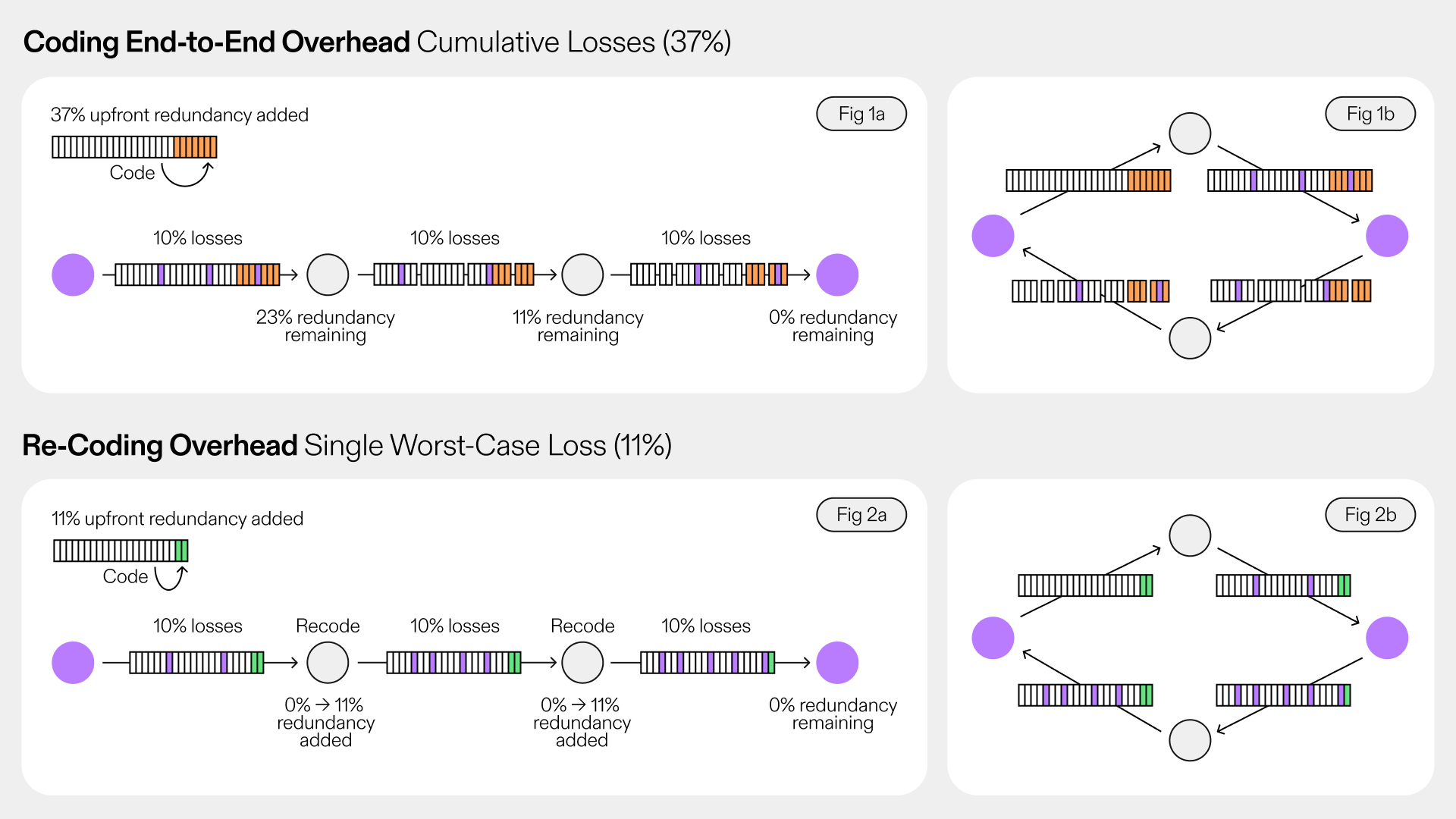
Communication over a wide area network (WAN) requires multiple hops, and often multiple paths exist between the source and the receiver. In such environments, both block and fountain codes may often fail to deliver the message. Both approaches assume that a single source is responsible for generating the coded elements from the original data, and therefore, a sufficient number of coded elements must reach the receiver to guarantee decodability. To do so, intermediate nodes need to forward the packets they receive. As shown in Figure 2(a), a (generally small) number of transmitted shards will be lost at each hop along the path from the source to the receiver. However, such loss is accumulated as the packets are passed from one hop to the next. So the more hops the packets need to travel, the more packets will be lost until they reach the receiver. The cumulative loss of encoded packets will either result in a failure of decodability or require substantial overhead.

One approach to cope with this is to decode the data at intermediate nodes, re-encode it, and then forward it to downstream nodes at each hop. While this may be feasible in simple networks, such as a daisy chain, it will fail in more complex topologies like the one shown in Figure 2(b). In such networks, splitting coded elements among intermediate nodes may prevent those nodes from collecting enough coded elements to decode.

In contrast, recoding at intermediate nodes when using Random Linear Network Coding (RLNC) — which does not require decoding — can actually assist in generating missing coded packets at each hop. As a result, the packet loss at the receiver will reflect only the losses incurred from the last hop. Consequently, the total loss remains comparable to that of a single-hop architecture. This ensures that decoding performance is preserved, allowing all data to be successfully decoded at the receiver. Furthermore, the network is fully utilized, as there is no downtime for decoding.

Owing to its ability to recode, RLNC is particularly well-suited for dynamic networks, where constant node churn and frequent changes in the path between source and receiver are common. Recoding in RLNC not only enables the creation of new encoded packets without prior decoding, but it also eliminates the need for distributed synchronization protocols, leveraging the inherent randomness of the coding process. This adaptability allows RLNC to dynamically optimize for changing network conditions, improving both latency and bandwidth efficiency.

Table 2: Scalability of RLNC, Reed-Solomon, and Fountain Codes

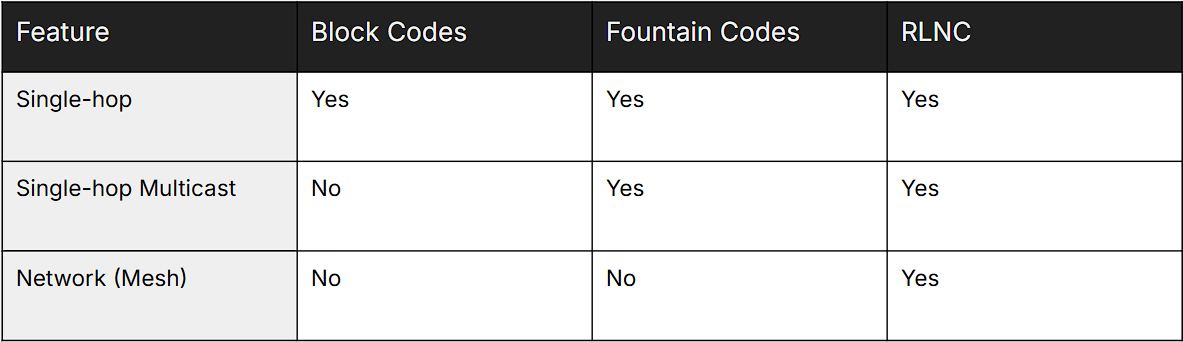
By harnessing the power of recoding, RLNC is uniquely equipped to handle scalability. In particular, all other coding approaches are unscalable. As the network grows, their throughput decreases with the number of hops, whereas RLNC is able to maintain a constant throughput. This means that it is necessary for a decentralized scalable network. In future pieces, we shall visit what are some of the practical consqeuences, even in cases where the number of hops is not large.

References

[ACLY00] Rudolf Ahlswede, Ning Cai, Shuo-Yen Robert Li, and Raymond W. Yeung. Network information flow. IEEE Transactions on Information Theory, 46(4):1204–1216, 2000.

[HMK+06] Tracey Ho, Muriel Médard, Ralf Kötter, David R. Karger, Michelle Effros, Jun Shi, and Ben Leong. A random linear network coding approach to multicast. IEEE Transactions on Information Theory, 52(10):4413–4430, 2006.

[KM03] Ralf K¨otter and Muriel M´edard. An algebraic approach to network coding. IEEE/ACM Transactions on Networking, 11(5):782–795, 2003.

[LJ04] Shu Lin and Daniel J. Costello Jr. Error Control Coding. Pearson Prentice Hall, 2nd edition, 2004.

[Lub02] Michael Luby. LT codes. In Proceedings of the 43rd Annual IEEE Symposium on Foundations of Computer Science (FOCS), pages 271–280, 2002.

[MAVPD25] Muriel Médard, Vipindev Adat Vasudevan, Morten Pedersen, and Ken Duffy. Network Coding for Engineers. 02 2025.

[RS60] Irving S. Reed and Gustave Solomon. Polynomial codes over certain finite fields. Journal of the Society for Industrial and Applied Mathematics, 8(2):300–304, 1960.

[Sho06] Amin Shokrollahi. Raptor codes. IEEE Transactions on Information Theory, 52(6):2551– 2567, 2006.