By Muriel Médard, Kishori Konwar, Nicolas Nicolaou

Abstract

In decentralized blockchain implementations, three properties are highly desirable: decentralization, security, and scalability. There is a widely held belief in the blockchain community—often referred to as the Blockchain Trilemma—that it is impossible to fully achieve all three simultaneously. As a result, much effort by protocol designers has focused on ensuring decentralization and security, while scalability has typically been left to be handled on a best-effort basis, with performance largely dependent on the processing and communication capacities of operators and participants. By leveraging the properties of Random Network Linear Coding (RLNC), we aim to enhance the scalability of any blockchain protocol while simultaneously improving decentralization and security, directly addressing the constraints imposed by current implementations.

The Trilemma Landscape: Navigating Competing Priorities

Blockchains emerged as one of the most popular distributed data structures after the introduction of Bitcoin in 2008 [18]. As per [2, 22], a blockchain can be considered an append-only data structure that stores a totally-ordered sequence of transactions. While relatively simple to implement on a single computing device, it becomes challenging to implement a blockchain in a decentralized manner using multiple, distinct, failure-prone (from crash to Byzantine failures) devices that communicate via messages.

Ethereum’s co-founder Vitalik Buterin [3] identified three properties as essential for the performance of distributed blockchain implementations: decentralization, referring to the large number of autonomous network devices that collectively implement and ensure the fault tolerance of the blockchain; security that refers to the implementation’s tolerance to malicious acts; and scalability that refers to the “speed” of the protocol in completing transactions. In the same article, Buterin introduced the term “Blockchain Trilemma”, raising concerns about the coexistence of these three properties. Buterin’s conjecture suggests that higher decentralization favors higher security, but negatively impacts scalability. Similarly, achieving higher scalability performance, requires either sacrificing decentralization for smaller networks or sacrificing security by bounding communication.

Following Buterin’s article [3], the blockchain community started seeking solutions to overcome the statement of the Trilemma and ensure the maximum performance for their proposed blockchain implementation. Let’s examine each property separately.

Decentralization. One of the core tenets used in blockchain implementations is decentralization, the distribution of control across a network of nodes rather than relying on a central authority. Decentralization offers multitudes of benefits: (i) tolerance of node failures, (ii) robustness against attacks as there are no sensitive central points, and (iii) resistance against node collusion when the majority of nodes are benign. In his article, Buterin [3], identified blockchains as architecturally and politically decentralized, yet logically centralized: they are built on top of multiple nodes (architectural decentralization), those nodes are controlled by multiple users (political decentralization), but the whole system needs to behave like a single device (logical centralization).

Protocols like Algorand [10] and Ethereum [7] aim to mitigate the challenges of decentralization, thereby avoiding the Trilemma and ensuring both security and scalability. Algorand [10] employs a protocol to reduce the number of nodes that participate in the consensus protocol. In contrast, sharding solutions, such as Danksharding [7], propose dividing the validators into smaller groups, each responsible to validate and agree on a different set of transactions.

Security. An adversary aims to violate the correctness of the system by either attempting to deviate the system from its sequential specification (and expected outcomes), or by preventing operations from terminating (i.e., denial of service). Buterin [3] identifies three potential security threats against blockchains:(i) Failures: when the adversary forces a set of nodes to stop operating, (ii) Attacks: malicious actions against a set of nodes to force them to diverge from the protocol, and (iii) Collusion: when nodes coordinate to “defeat” the protocol.

Protocols were also designed to deal with security concerns, and address the Trilemma conjecture. Such solutions can be found in optimistic rollups [13] and private pools [14]. Optimistic rollups were introduced to address security constraints while improving scalability performance. They propose collecting and validating transactions off-chain, and the submission of a collective outcome to the main chain. They follow all the security rules of the main chain and ensure that collected transactions are secure. Private pools, on the other hand, ensure security by assigning validation to a verified, whitelisted group of validators.

Scalability. Decentralization and security are crucial for the reliability of the blockchain, but scalability is an essential metric for its performance. Scalability captures the system’s capacity to handle increasing operational demands without compromising speed or cost-efficiency. A scalable blockchain should process a high throughput of transactions (measured in transactions per second) while keeping fees low and confirmation times fast, ideally without requiring excessive computational resources or centralization trade-offs. Since a blockchain is built on top of message-exchanging nodes, transaction latency is heavily dependent on the delay in delivering the messages required to complete a single transaction, which directly influences transaction throughput.

Contrary to decentralization and security, developers and providers of blockchains have not designed or considered protocol solutions to directly tackle transaction latency and enhance scalability at the network level. Instead, they rely on probabilistic and best effort scalability, which is driven by incentives provided to network maintainers and participants to boost their computation and/or network capabilities. Traditional blockchains like Bitcoin and Ethereum [1, 9], solely rely on the network’s capabilities, providing network-dependent scalability.

To improve upon simple network performance, some Ethereum Layer 2 solutions, like rollups [13], propose the utilization of computationally intensive nodes for merging together multiple transactions into a single transaction before committing the merged transaction onto the main chain. Those nodes are incentivized through rewards, based on the efficiency of their transaction merging process. Solana [23], on the other hand, incentivizes validator participation: a node may participate as a validator and receive rewards only if it offers high computational and network capabilities. In that sense, Solana relies on costly high-performance machines to deliver scalability. However, such solutions are still susceptible to network delays.

What are the limitations of best-effort scalability? Can we guarantee the completion of every transaction? Are those transactions completing quickly enough?

Scalability with Provable Guarantees

Ideally, we need solutions that offer provable guarantees on scalability performance. To achieve this, we first need to understand the key components and latency bottlenecks of blockchain transactions. The most important mechanism of every blockchain is to allow system maintainers to agree on a single sequence of transactions. This ensures that the system eventually reaches a stable and consistent state. Consequently, a State Machine Replication (SMR) [15] service is the backbone of all major blockchain implementations. Each node in the system executes the same operations in the same order, ultimately leading all nodes to the same state, which reflects the overall state of the system.

Significance of Consensus. To facilitate agreement on operations and their order, blockchain implementations address SMR by solving the consensus problem [16, 20]. Consensus is a well-known problem in distributed systems, where every node proposes a value, and all nodes must agree on one of the proposed values. The correctness of a consensus algorithm is governed by three requirements: (i) agreement: every node must decide on the same value. (ii) validity: the decided value must have been proposed by a node. (iii) termination: eventually, every node must decide a value. Agreement and validity define the safety, and termination the liveness properties of consensus. In the context of blockchains, nodes need to agree on the transaction blocks and the order in which they will be appended to the chain.

Unsolvability of Consensus. Fischer, Lynch, and Paterson (FLP) in [8] showed that fault-tolerant agreement is impossible to guarantee with certainty in an asynchronous system with the crash failure of a single node.

Solvability of Consensus. Following the FLP result, researchers focused on exploring how synchronicity may affect the solvability of consensus. Soon it was shown that consensus can be solved in synchronous fault-prone systems where nodes compute in sync, messages are delivered within known timing bounds, and execution proceeds in synchronous rounds. It was shown [17, 5] that f + 1 rounds, where f, the maximum number of nodes that may be byzantine or crash, are sufficient to solve consensus in the synchronous system. This triggered the question: How much synchrony is necessary to solve consensus?

Living in Partial Synchrony. Soon after [8], Dwork, Lynch, Stockmeyer [6], proposed an algorithm for solving consensus in a partial or eventual synchronous system, i.e. a system that experiences both periods of synchrony and some periods of asynchrony. As long as such a system eventually stabilizes and offers “long enough” windows of synchrony, we can solve consensus. It is noteworthy that the algorithm proposed by Dwork, Lynch, Stockmeyer [6], nearly three decades ago, serves as the fundamental algorithm employed in any Tendermint/CometBFT based SMR system [12]. Other prominent blockchains, such as Ethereum, Solana, BNB Chain, Cosmos-based chains, and others, also rely on partial synchrony to resolve leader-based consensus. Each leader needs to make decisions within a predefined time interval ∆,usually known as block time. Consequently, ∆ represents the synchrony window duration within which consensus must be solved. The value of ∆ is known to the nodes and is used to decide when it's time to move to the next consensus slot.

Timing Decisions. But what is the best ∆? Picking a large ∆ may delay the consensus decision, and in turn block finality and reduce transaction throughput and scalability. Very small values for ∆ may result in unproductive consensus attempts and thereby again decreasing throughput. Thus, there is a tradeoff involved in reducing the consensus slot Δ while potentially increasing the number of transactions finalized in a given time interval.

Consensus algorithms involve each node attempting to communicate its local value to the others, through a series of message exchanges. Similar to information propagation in social networks, gossip is used for propagating the proposed values among the nodes. Due to network disruptions, some messages may be lost, some may be delayed, some may be received at a node from multiple origins (i.e., duplicated), and some may be retransmitted. Such incidents may increase the time needed for information propagation and hence reaching consensus, inevitably resulting in large ∆ slots especially in larger networks. This motivates the decision in many blockchain solutions to limit decentralization for scalability.

The Promise of RLNC. In order to scale without compromising decentralization, it becomes necessary to devise low latency gossip (publish/subscribe) solutions to reduce the ∆ slot. Random Linear Network Codes (RLNC) [11], propose the division of message data into coded elements using algebraic equations over finite fields. To compensate for network losses and malicious (Byzantine) behavior, RLNC requires each node to collect only a subset of the generated coded elements (or equations) for recovering the original message. Furthermore, RLNC eliminates duplicates by enabling each intermediate node to randomly combine equations on the fly and generate novel, previously unseen coded elements. Consequently, each node discovers new information with every coded element received. These characteristics render RLNC resilient to decentralization, and (provably) achieve optimal throughput for message transfers [4].

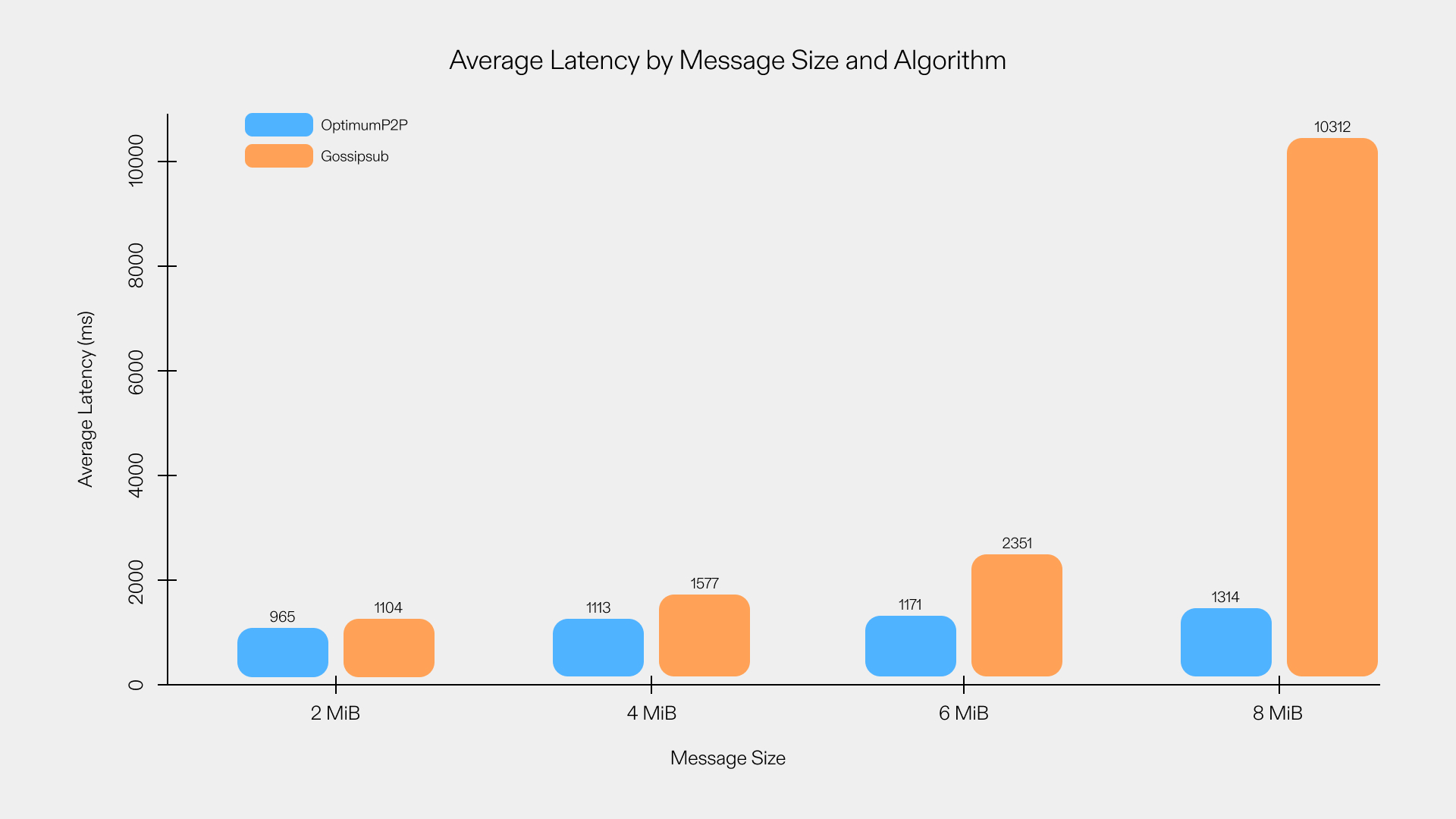
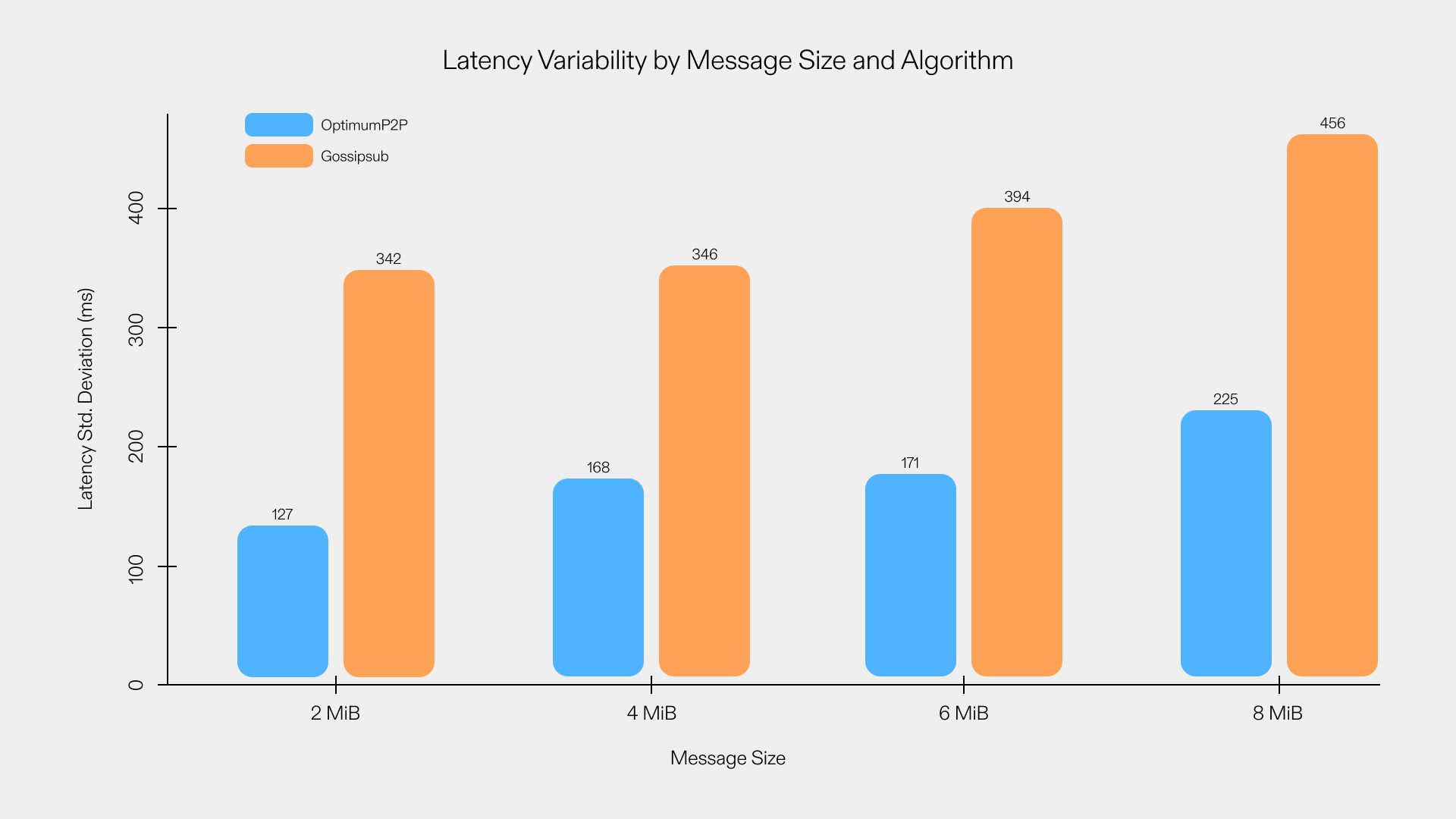
As a result, RLNC enhances message delivery, reducing the consensus slot ∆ while making an increase to the number of transactions finalized within a given time interval possible. This implies scalability benefits without compromising either decentralization or security within the system.

We have proposed, implemented, and deployed a preliminary version of a new data propagation protocol called OptimumP2P, that extends the widely used Gossipsub protocol and incorporates RLNC at its core. We have compared OptimumP2P’s and Gossipsub’s performance in terms of latency and average delay. Our observations indicate that OptimumP2P offers substantial improvements. Analytical and experimental results (see plots and [19]) consistently demonstrate that gossiping with RLNC reduces both the average and the standard deviation of message propagation times across large networks. As the next step, we are planning to bring OptimumP2P to the service of current blockchain implementations, like Ethereum, by designing architectures to seamlessly integrate OptimumP2P with Ethereum validators allowing them to achieve higher throughput, lower latency and hence higher scalability.

Conclusions

With RLNC, a chain’s scalability becomes untethered from its decentralization and security, free from the binds of the classic trilemma.

OptimumP2P leverages RLNC, unlocking the trilemma by raising network performance and maintaining high performance as message sizes increase, while also keeping bandwidth requirements for network participants low. In practice this enables throughput scaling via larger blocks and shorter slot times, achieving the speed that users value so highly without the need to centralize the network.

References

[1] What is bitcoin fork? http://blog.cex.io/bitcoin-dictionary/what-is-bitcoin-fork-14622. Accessed: 2016-05-05.

[2] Anta, A. F., Konwar, K. M., Georgiou, C., and Nicolaou, N. C. Formalizing and implementing distributed ledger objects. SIGACT News 49, 2 (2018), 58–76.

[3] Buterin, V. The meaning of decentralization. Medium (Feb 2017). Accessed: May 2025.

[4] Deb, S., Medard, M., and Choute, C. Algebraic gossip: a network coding approach to optimal multiple rumor mongering. IEEE Transactions on Information Theory 52, 6 (2006), 2486–2507.

[5] Dolev, D., and Strong, H. R. Authenticated algorithms for byzantine agreement. SIAM Journal on Computing 12, 4 (1983), 656–666.

[6] Dwork, C., Lynch, N., and Stockmeyer, L. Consensus in the presence of partial synchrony. J. ACM 35, 2 (1988), 288–323.

[7] Feist, D. Danksharding. Ethereum Research (2022). Ethereum Research post introducing Dankshard-ing.

[8] Fischer, M. J., Lynch, N. A., and Paterson, M. S. Impossibility of distributed consensus with one faulty process. Journal of ACM 32, 2 (1985), 374–382.

[9] Foundation, E. Ethereum 2.0 networking specification. https://github.com/ethereum/consensus-specs, 2023. Accessed: 2023-10-10.

[10] Gilad, Y., Hemo, R., Micali, S., Vlachos, G., and Zeldovich, N. Algorand: Scaling byzantine agreements for cryptocurrencies. In Proceedings of the 26th Symposium on Operating Systems Principles (New York, NY, USA, 2017), SOSP ’17, Association for Computing Machinery, p. 51–68.

[11] Ho, T., Medard, M., K¨otter, R., Karger, D. R., Effros, M., Shi, J., and Leong, B. A random linear network coding approach to multicast. IEEE Transactions on Information Theory 52, 10 (2006), 4413–4430.

[12] Jae Kwon. Tendermint: Consensus without mining. https://tendermint.com/static/docs/tendermint.pdf, n.d. Accessed: July 7, 2025.

[13] Kalodner, H., Goldfeder, S., Chen, X., Weinberg, S. M., and Felten, E. W. Arbitrum: Scalable, private smart contracts. Proceedings of the 27th USENIX Security Symposium (2018), 1353–1370. Introduces optimistic rollups via Arbitrum’s fraud-proof mechanism.

[14] Labs, U. Uniswap v4: The future of amms, 2023. Introduces customizable pools, including private variants.

[15] Lamport, L. Time, clocks, and the ordering of events in a distributed system. Communications of the ACM 21, 7 (1978), 558–565.

[16] Lamport, L., Shostak, R., and Pease, M. The byzantine generals problem. ACM Transactions on Programming Languages and Systems (TOPLAS) 4, 3 (1982), 382–401.

[17] Lynch, N. A., and Fischer, M. J. Lower bounds on the time to assure interactive consistency. Information Processing Letters 16, 4 (May 1983), 187–189.

[18] Nakamoto, S. Bitcoin: A peer-to-peer electronic cash system.

[19] Optimum. Comparing the performance of optimump2p and gossipsub, 2025.

[20] Pease, M., Shostak, R., and Lamport, L. Reaching agreement in the presence of faults. Journal of the ACM (JACM) 27, 2 (1980), 228–234.

[21] Raynal, M. Fault-tolerant message-passing distributed systems.

[22] Roughgarden, T. Foundations of blockchains lectures, 2022.

[23] Solana Labs. Solana: Fast, secure, decentralized blockchain. https://solana.com, n.d.