Introduction: The Determinism Challenge in AO and the Summation Operator

The AO ecosystem, built on Arweave, aims to achieve decentralized, trustless computation. APUS Network, as a GPU acceleration project within AO, focuses on enhancing the efficiency of compute-intensive tasks like deep learning. However, a key challenge in decentralized systems like AO is ensuring the determinism of computation results. Non-determinism—where the same input might produce slightly different outputs across different runs or hardware—undermines the verifiability and trust required for decentralized platforms.

This blog post focuses on one of the most fundamental operations in deep learning: the summation operator. We will explore the non-determinism issues it faces under GPU acceleration and introduce the work APUS Network is doing to address this problem.

The Challenge: Non-Determinism in GPU Summation

Summation (or reduction) is a foundational operation in deep learning, widely used in dot products, normalization layers, loss calculations, and more. When executed on parallel hardware like GPUs, standard summation algorithms often encounter non-determinism issues, primarily due to:

1. Floating-Point Arithmetic Properties: IEEE 754 floating-point numbers have limited precision, and crucially, addition is not associative. That is, (a + b) + c is not always bit-wise identical to a + (b + c) due to intermediate rounding errors.

2. Parallel Reduction Order: GPUs accelerate computations by processing vast amounts of data in parallel. Optimized reduction algorithms (like those in PyTorch or TensorFlow) distribute the input among many threads and combine partial sums using parallel tree structures. The exact order in which these partial sums are combined can vary depending on thread scheduling and hardware specifics, leading to different accumulations of rounding errors and thus different final results.

3. Atomic Operations: Some parallel algorithms use atomic operations to allow multiple threads to update the same memory location (the running sum). The order in which threads execute these atomic updates is inherently non-deterministic, again affecting the final result.

Even when frameworks provide options to enforce determinism (e.g., torch.use_deterministic_algorithms(True)), they typically enforce a specific parallel strategy but may not fully mitigate the precision issues inherent in naive summation, especially with large datasets or data with a wide dynamic range.

Code Example: Demonstrating Non-Determinism

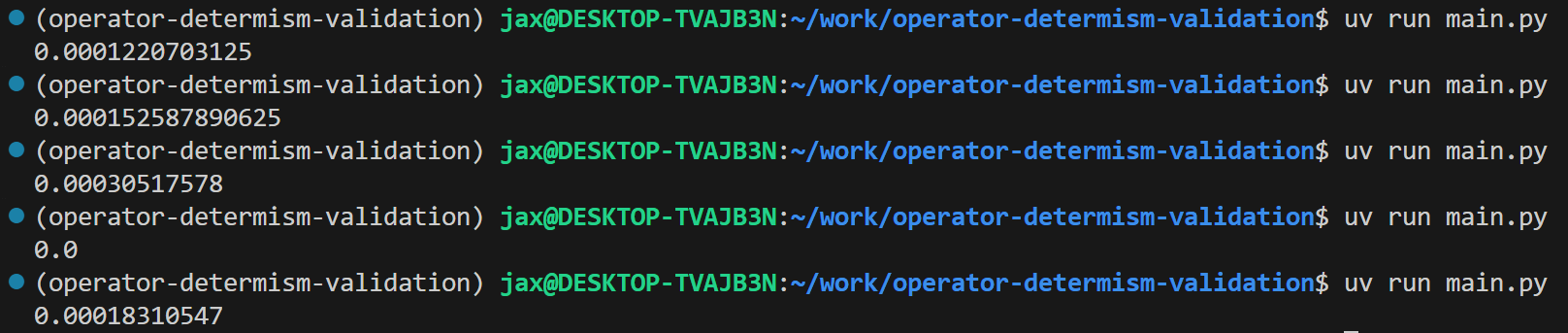
We can observe this non-determinism with a simple PyTorch snippet. The following code (derived from main.py) attempts to sum the same random array on both the GPU and CPU. Even with determinism flags set, minor differences can arise due to underlying implementation variations, especially between CPU and GPU floating-point units:

We can observe this non-determinism with a simple PyTorch snippet. The following code (derived from main.py) attempts to sum the same random array on both the GPU and CPU. Even with determinism flags set, minor differences can arise due to underlying implementation variations, especially between CPU and GPU floating-point units:

import torch
import numpy as np

# Attempt to enforce deterministic algorithms
# Note: This primarily affects PyTorch's internal algorithm choice.
# Subtle differences in CPU vs. GPU floating-point hardware can still cause variations.
torch.use_deterministic_algorithms(True)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False # Disable benchmarking to reduce variability

x_gpu = torch.randn(1000000, device='cuda', dtype=torch.float32)

# GPU Summation
gpu_sum = x_gpu.sum().item()

# CPU Summation (Move data to CPU)
cpu_sum = x_gpu.cpu().sum().item()

# Compare results (use np.float32 for consistent comparison precision)
difference = abs(np.float32(cpu_sum) - np.float32(gpu_sum))

print(f"GPU Sum: {gpu_sum}")
print(f"CPU Sum (Reference): {cpu_sum}")
print(f"Difference: {difference}")

Deterministic Solution: Kahan Summation with CUDA (Khana_Sum)

To guarantee bit-wise identical summation results regardless of execution order, we need an algorithm that actively compensates for floating-point rounding errors. The Kahan summation algorithm is a well-known technique for this. It maintains a running compensation term (c) to track and correct for the error introduced in each addition step.

APUS Network has implemented and verified a deterministic Kahan summation algorithm accelerated using CUDA.

Implementation (kahan_sum.cu)

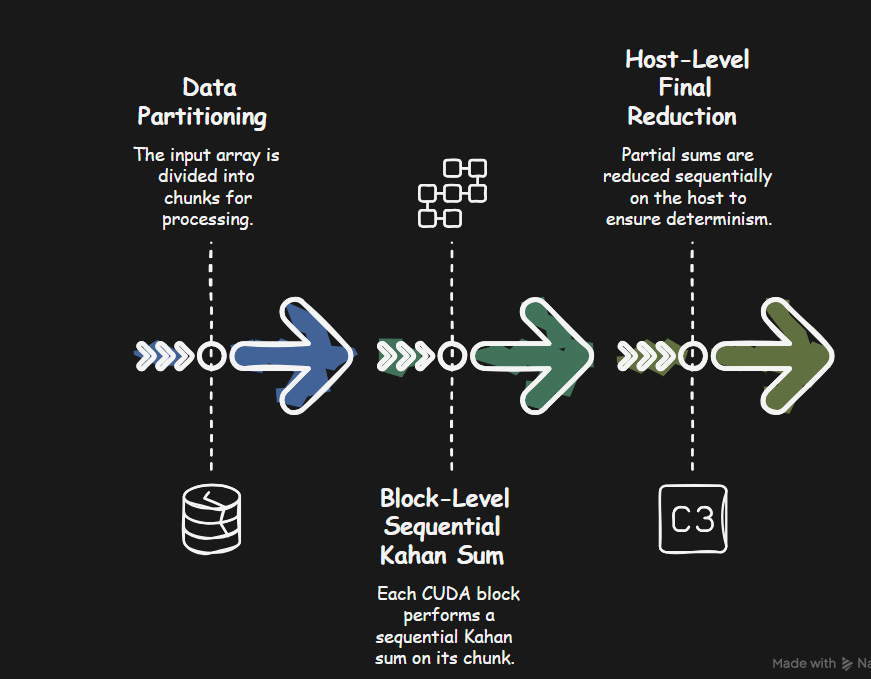
The core idea is to combine parallelism with the sequential nature of Kahan summation carefully:

1. Data Partitioning: The input array is conceptually divided into chunks.

2. Block-Level Sequential Kahan Sum: A CUDA kernel (kahan_block_sum) is launched where each CUDA block is assigned a chunk of the input data. Crucially, within each block, only a single thread (threadIdx.x == 0) performs a sequential Kahan sum over its assigned chunk. This avoids the non-determinism associated with parallel reduction trees within the block. Each block outputs its partial sum (block_sums) and the final compensation term (block_compensations) for its chunk.

   // CUDA kernel to perform Kahan summation for a block's chunk of data
   __global__ void kahan_block_sum(const float* input, int n, int chunk_size, float* block_sums, float* block_compensations) {
       // Ensure only thread 0 of the block executes the sequential sum
       if (threadIdx.x == 0) {
           int block_start_idx = blockIdx.x * chunk_size;
           int block_end_idx = min(block_start_idx + chunk_size, n);
   
           float sum = 0.0f;
           float c = 0.0f;
           
           for (int i = block_start_idx; i < block_end_idx; ++i) {
               float x = input[i];
               float y = x - c;
               float t = sum + y;
               c = (t - sum) - y;
               sum = t;
           }
   
           block_sums[blockIdx.x] = sum;
           block_compensations[blockIdx.x] = c;
       }
   }
   

3. Host-Level Final Reduction: The partial sums calculated by each block (h_block_sums) are copied back to the host (CPU). A final Kahan summation (kahan_sum_host, called within run_kahan_sum_cuda) is performed sequentially on the host over these partial sums. Since this final step is purely sequential, it is deterministic.

   // Host-side function in kahan_sum.cu (Simplified Snippet)
   extern "C" float run_kahan_sum_cuda(const float* h_input, int n) {
       // ... (Allocate device memory, copy input) ...
   
       int chunk_size = 4096; // Example chunk size
       int num_blocks = (n + chunk_size - 1) / chunk_size; // Calculate number of blocks needed
   
       // Allocate host memory for results from blocks
       float* h_block_sums = (float*)malloc(num_blocks * sizeof(float));
       // ... (Allocate block_compensations memory) ...
   
       // Allocate device memory for block results
       float* d_block_sums;
       // ... (Allocate d_block_compensations) ...
       cudaMalloc((void**)&d_block_sums, num_blocks * sizeof(float));
       // ...
   
       // Launch kernel
       kahan_block_sum<<<num_blocks, 1>>>(/*...*/ d_block_sums, /*...*/);
       cudaDeviceSynchronize(); // Wait for GPU to finish
   
       // Copy block sums back to host
       cudaMemcpy(h_block_sums, d_block_sums, /*...*/);
   
       // Perform final Kahan sum on the host over the block sums
       float final_reduction_sum = kahan_sum_host(h_block_sums, num_blocks);
   
       // ... (Free memory) ...
       return final_reduction_sum;
   }
   

This hybrid approach leverages GPU parallelism for the bulk of the work (processing chunks) while ensuring determinism by performing the Kahan summation steps sequentially within blocks and during the final reduction on the host.

Verification (kahan_sum.py)

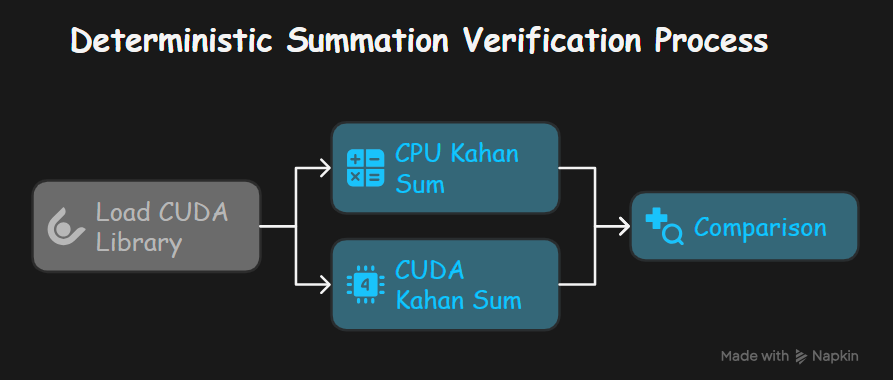
To validate the implementation, a Python script (kahan_sum.py) compares the result of the CUDA Kahan sum with a pure NumPy-based Kahan sum executed on the CPU.

1. Load CUDA Library: The compiled CUDA code (kahan_sum_cuda.so) is loaded using ctypes.

2. CPU Kahan Sum: A reference implementation kahan_sum_cpu performs the algorithm using NumPy with np.float32 precision.

3. CUDA Kahan Sum: The run_kahan_sum_cuda function from the loaded library is called with the input data.

4. Comparison: The results from the CPU and CUDA implementations are compared.

# Snippet from kahan_sum.py
import ctypes
import numpy as np
import os

# --- Load the compiled CUDA library ---
lib_name = 'kahan_sum_cuda.so'
# ... (construct lib_path) ...
kahan_lib = ctypes.CDLL(lib_path)
# ... (define argtypes and restype) ...

# --- CPU Kahan Sum Implementation ---
def kahan_sum_cpu(arr):
    sum_ = np.float32(0.0)
    c = np.float32(0.0)
    for x in arr:
        y = np.float32(x - c)
        t = np.float32(sum_ + y)
        c = np.float32((t - sum_) - y)
        sum_ = np.float32(t)
    return sum_

# --- Prepare Data and Run ---
data_size = 1000000
data_cpu = np.random.rand(data_size).astype(np.float32)
c_float_array = (ctypes.c_float * data_size)(*data_cpu.tolist())

# Calculate sums
result_cpu = kahan_sum_cpu(data_cpu)
cuda_kahan_sum = np.float32(kahan_lib.run_kahan_sum_cuda(c_float_array, data_size))

# Verify
print("CPU Kahan Sum:", result_cpu)
print("CUDA Kahan Sum:", cuda_kahan_sum)
print("Difference:", abs(result_cpu - cuda_kahan_sum))

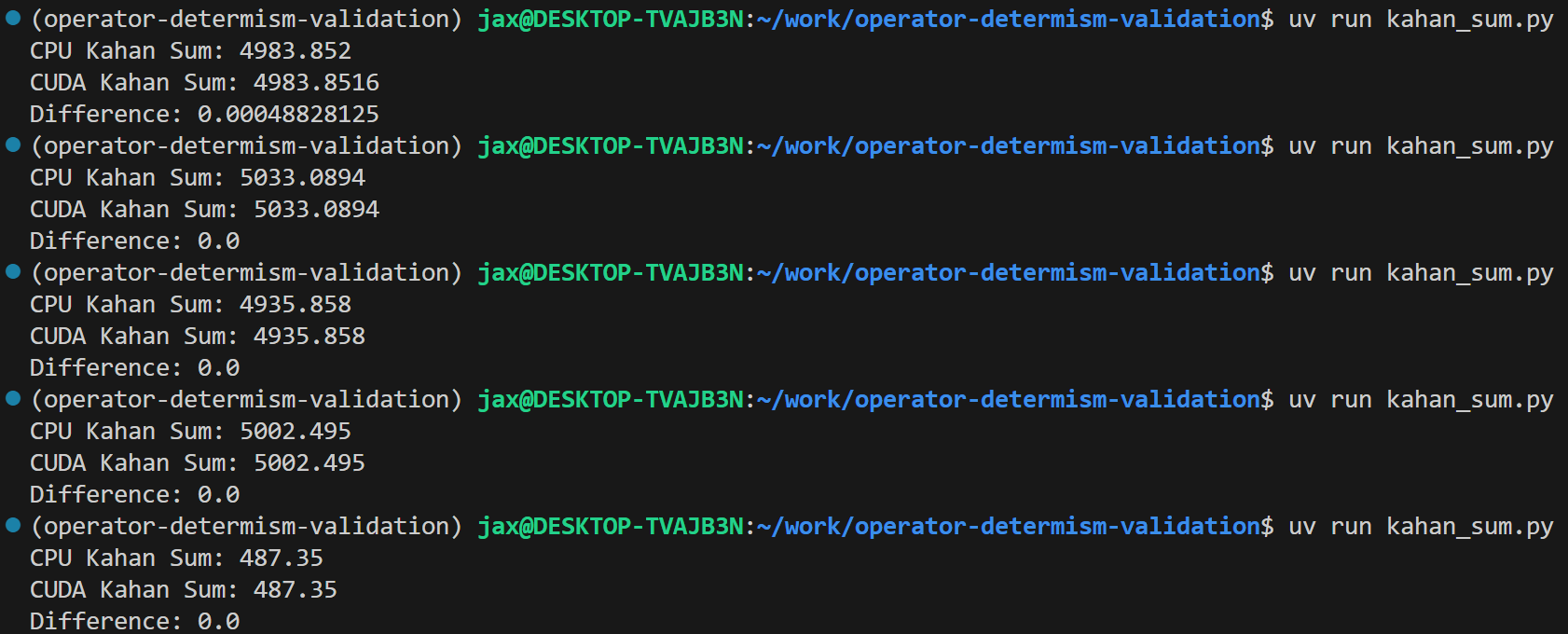
The script consistently shows a difference of 0.0, confirming that the CUDA implementation produces bit-wise identical results to the deterministic CPU Kahan summation.

Performance and Costs

Ensuring determinism comes at a cost. Kahan summation involves more operations per element than a naive sum. Furthermore, the chosen CUDA implementation uses only one thread per block for the actual summation and involves copying partial results back to the host for the final reduction. This is generally slower than highly optimized, potentially non-deterministic parallel reduction algorithms (like cub::BlockReduce or standard torch.sum implementations).

However, for decentralized systems like AO where verifiability is paramount, the cost of ensuring determinism through methods like Kahan summation is often a necessary trade-off.

Conclusion: Balancing Performance and Determinism for AO

Non-determinism in fundamental operations like summation poses a significant barrier to integrating reliable AI inference into decentralized systems like AO. APUS Network is tackling this challenge by developing and verifying deterministic implementations of core operators, as demonstrated with the CUDA-accelerated Kahan summation.

While standard GPU libraries often prioritize raw speed at the expense of strict reproducibility, solutions like the Kahan sum implementation provide the bit-wise determinism crucial for trust and verifiability within the AO ecosystem. This work represents a concrete step towards building a foundation for fully deterministic AI inference (as envisioned by concepts like DCAIP), enabling complex, verifiable AI applications to run reliably on AO. APUS Network will continue to explore and implement solutions that carefully balance the need for performance with the non-negotiable requirement