A hash tree, also known as the Merkle Tree, is a cryptographic structure fundamental to blockchain technology. It is a tree with each leaf node labelled with the hash value of a data block, and each non-leaf node labelled with the hash value of its child nodes labels.

This article discusses various aspects of Merkle trees, highlighting their significance in ensuring the integrity and security of data within a blockchain. The discussion holds topics such as:

• Cryptographic hash functions

• Blockchain structure

• Merkle tree construction

• Proof of membership

• Merkle proofs, and the advantages conferred by Merkle trees.

Let’s discuss each of these topics in detail.

What is a Cryptographic Hash?

A cryptographic hash function is a tool in blockchain technology, that generates fixed-size digests for variable-length inputs. Hash functions, such as SHA-256, produce unique outputs for different inputs, making them important for verifying data integrity.

Even minor alterations in input data produce dramatically different hash values, helping in the detection of tampering.

From the above picture, it is clear that the slightest change in the alphabet in the input sentence can drastically change the hash obtained. Therefore hashes can be used to verify integrity.

Imagine you have a text file containing crucial data. You pass the contents of this file through a hash function, which generates a unique hash value. This hash value is then stored on your phone.

However, if a hacker gains access to the file and alters its data, upon reopening the file, you can recompute the hash value and compare it with the previously stored hash. Any discrepancy between the two hash values would indicate that the file has been tampered with.

What is Hash Pointer?

A conventional pointer simply stores the memory address of data, promoting easy access to that data.

In contrast, a hash pointer not only points to where data is stored but also includes the cryptographic hash of the data alongside it. This means that a hash pointer not only directs us to the data but also enables us to verify its integrity.

Utilizing hash pointers, various data structures such as blockchains and Merkle trees can be constructed, leveraging the ability to securely reference and verify data within these structures.

Blockchain Structure Explained

The blockchain is a proficient combination of two hash-based data structures-

1. Linked list: This is the structure of the blockchain itself, which is a linked list of hash pointers. Unlike a conventional linked list, where each node contains data and a pointer to the next node, in a blockchain, the traditional pointer is substituted with a hash pointer. This hash pointer not only directs to the next block but also verifies the integrity of the data.

Merkle Tree: A Merkle tree is a binary tree formed by hash pointers, and named after its creator, Ralph Merkle.

The Structure of a Block

1. Block Header -

   The header data contains metadata of the block, i.e. information about the block itself.

   The contents of the block header include -

   1. The hash of the previous block header.

   2. The hash of the current block.

   3. Timestamp.

   4. Cryptographic nonce.

   5. Merkle root.

2. Merkle Tree -

   A Merkle tree is a binary tree formed by hash pointers and named after its creator, Ralph Merkle.

   As mentioned earlier, each block is supposed to hold a certain number of transactions. Now the question arises, how to store these transactions within a block?

   One approach can be to form a hash pointer-based linked list of transactions and store this complete linked list in a block. However, when we put this approach into perspective, it does not seem practical to store an extensive list of hundreds of transactions.

   What if there is a need to find whether a particular transaction belongs to a block? Then we will have to traverse the blocks one by one, and within each block, traverse the linked list of transactions. This approach can reduce the efficiency of the blockchain.

   Now, this is where the Merkle tree comes into the picture. It serves as a per-block tree structure that includes all the transactions within the block. By organizing transactions in a tree-like fashion and computing hashes at each level, the Merkle tree enables the generation of a single hash or digest representing all transactions within the block.

   So to recap, the blockchain is a hash-based linked list of blocks, where each block consists of a header and transactions. The transactions are arranged in a tree-like fashion, known as the Merkle tree.

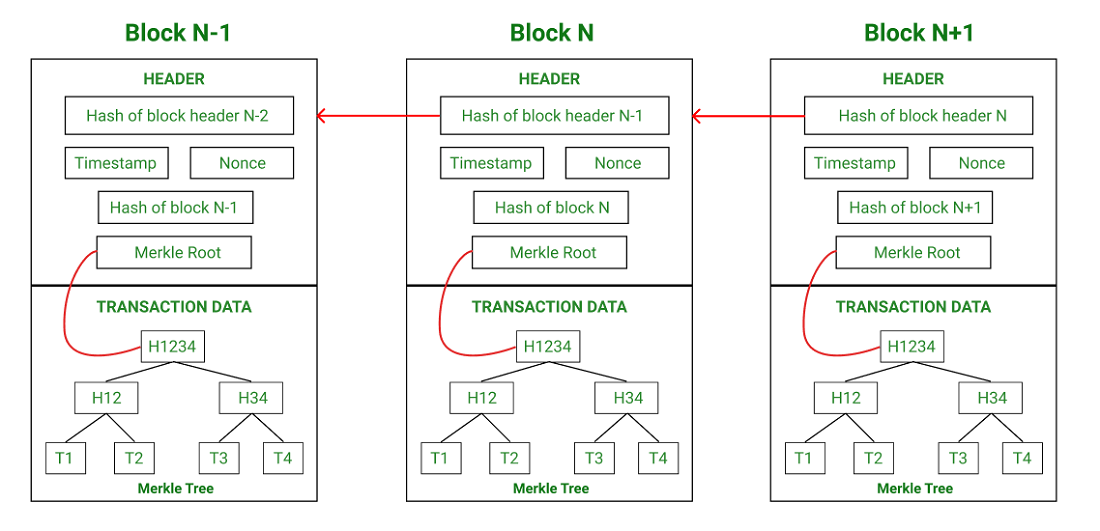
Merkle Tree Structure

A blockchain can potentially have thousands of blocks with thousands of transactions in each block. Therefore, memory space and computing power are two main challenges.

It would be optimal to use as little data as possible for verifying transactions, which can reduce CPU processing and provide better security, and this is exactly what Merkle trees offer.

In a Merkle tree, transactions are grouped into pairs. The hash is computed for each pair and this is stored in the parent node. The parent nodes are grouped into pairs and their hash is stored one level up in the tree. This continues till the root of the tree.

Bitcoin uses the SHA-256 hash function to hash transaction data continuously till the Merkle root is obtained.

Further, a Merkle tree is binary in nature. This means that the number of leaf nodes needs to be even for the Merkle tree to be constructed properly. In case there is an odd number of leaf nodes, the tree duplicates the last hash and makes the number of leaf nodes even.

Different Types of Nodes in a Merkle Tree

• Root node: The root of the Merkle tree is known as the Merkle root and is stored in the header of the block.

• Leaf node: The leaf nodes contain the hash values of transaction data. Each transaction in the block has its data hashed. This hash value (also known as transaction ID) is stored in leaf nodes.

• Non-leaf node: The non-leaf nodes contain the hash value of their respective children. These are also called intermediate nodes because they contain the intermediate hash values. Thereafter, the hash process continues till the root of the tree.

How Do Merkle Trees Work?

Think of building a Merkle tree-like constructing a pyramid, starting from the bottom and moving upwards. You begin with the individual transactions at the leaf nodes, then group them in pairs and calculate the hash for each pair. These hash values represent the combined integrity of the paired transactions.

As you move up a level, each pair's hash is further hashed together, creating a new level of hashes. This process continues until you reach the Merkle root at the top, the ultimate hash representing all transactions in the block.

Comparing this construction to a typical binary tree, where branches extend downwards, Merkle trees are built "upside-down". The hash values flow upwards, with each level representing a summary of the data below it. This inverted structure provides a streamlined way to verify transactions and ensure the integrity of the blockchain data.

Constructing a Merkle Tree for a Block

Consider a block having 4 transactions- T1, T2, T3, T4. These four transactions have to be stored in the Merkle tree and this is done by the following steps-

Step 1: Compute Transaction Hashes

The hash of each transaction is computed.

H1 = Hash(T1).

Step 2: Store Hashes in Leaf Nodes

The hashes computed are stored in leaf nodes of the Merkle tree.

Step 3: Form Non-Leaf Nodes

Now non-leaf nodes will be formed. To form these nodes, leaf nodes will be paired together from left to right, and the hash of these pairs will be calculated.

Firstly, the hash of H1 and H2 will be computed to form H12. Similarly, H34 is computed. Values H12 and H34 are parent nodes of H1, H2, and H3, H4 respectively. These are non-leaf nodes.

H12 = Hash(H1 + H2)

H34 = Hash(H3 + H4)

Step 4: Compute Merkle Root

Finally, H1234 is computed by pairing H12 and H34. H1234 is the only hash remaining. This means we have reached the root node and therefore H1234 is the Merkle root.

H1234 = Hash(H12 + H34)

Ensuring Transaction Integrity with Merkle Roots in Blockchain

In the context of blockchain security, the Merkle root plays an important role in safeguarding the integrity of transactions within a block.

By storing only the Merkle root in the block header, the blockchain system efficiently verifies the authenticity of transactions without needing to store each transaction individually. This approach generates a digital fingerprint of all transactions, allowing for validation of the entire block's contents.

Mechanism of Merkle Root Verification:

• Tamper-Proofing Transactions: Changes in any transaction within the block are reflected in the corresponding hashes up the Merkle tree hierarchy.

• Propagation of Changes: Altered transaction data affects the hash values of parent nodes, moving upwards until reaching the Merkle root.

• Root as a Verification Point: If the Merkle root changes, it indicates tampering with the transactions, alerting the system to the compromised data integrity.

• Enhanced Security with Block Header Hash: Further protection is provided by hashing the block header, including the Merkle root, and storing it in the subsequent block.

Why are Merkle Trees Important for Blockchain?

In a centralized network, data can be accessed from a single copy. This means that nodes do not have to take the responsibility of storing their copies of data and data can be retrieved quickly.

However, the situation is not so simple in a distributed system.

Let us consider a scenario where blockchain does not have Merkle trees. In this case, every node in the network will have to keep a record of every single transaction that has occurred because there is no central copy of the information.

This means that a huge amount of information will have to be stored on every node and every node will have its copy of the ledger. If a node wants to validate a past transaction, requests will have to be sent to all nodes, requesting their copy of the ledger.

Thereafter, the user will have to compare its copy with the copies obtained from several nodes. Any mismatch could compromise the security of the blockchain.

Furthermore, such verification requests will require large amounts of data to be sent over the network, and the computer performing this verification will need a lot of processing power for comparing different versions of ledgers.

Without the Merkle tree, the data itself has to be transferred all over the network for verification.

Merkle trees allow the comparison and verification of transactions with viable computational power and bandwidth. Only a small amount of information needs to be sent, hence compensating for the huge volumes of ledger data that had to be exchanged previously.

Merkle trees use a one-way hash function extensively and this hashing separates the proof of data from the data itself

Proof of Membership

An interesting aspect of Merkle trees is their ability to provide proof of membership, an important feature in blockchain systems. For instance, let's say a miner needs to demonstrate that a specific transaction is indeed part of a Merkle tree. In such cases, the miner only needs to have the following elements:

• Transaction: The particular transaction in question.

• Nodes on Path: All intermediary nodes lying along the path from the transaction up to the root of the Merkle tree.

By providing these components, the miner offers solid proof that the transaction is legitimately included in the Merkle tree. This proof allows any verifier to efficiently confirm the transaction's validity by recalculating the hashes using the presented data.

What's fascinating is that only a fraction of the entire tree needs to be examined for verification. The rest of the tree can be safely ignored, as the hashes stored in the intermediary nodes contain ample information to verify the transaction's integrity up to the root.

If there are n nodes in the tree then only log(n) nodes need to be examined. Hence, even if there are a large number of nodes in the Merkle tree, proof of membership can be computed in a relatively short time.

Proof of Non-Membership

It is also possible to test non-membership in logarithmic time and space using a sorted Merkle tree. That is, it is possible to show that a given transaction does not belong in the Merkle tree.

This can be done by displaying a path to the transaction that is immediately before the transaction in question, as well as a path to the item that is immediately following it.

If these two elements in the tree are sequential, this proves that the item in issue is not included or else it would have to go between the two things shown if it was included, but there is no room between them because they are sequential.

What are Merkle Proofs?

A Merkle proof is used to decide:

1. If data belongs to a particular Merkle tree.

2. To prove data belongs to a set without the need to store the whole set.

3. To prove that certain data is included in a larger data set without revealing the larger data set or its subsets.

Merkle proofs are established by hashing a hash’s corresponding hash together and climbing up the tree until you obtain the root hash which is or can be publicly known.

Consider the Merkle tree given below:

Let us say we need to prove that transaction ‘a’ is part of this Merkle tree. Everyone in the network will be aware of the hash function used by all Merkle trees.

1. H(a) = Ha as per the diagram.

2. The hash of Ha and Hb will be Hab, which will be stored in an upper-level node.

3. Finally, the hash of Hab and Hcd will give Habcd. This is the Merkle root obtained by us.

4. By comparing the obtained Merkle root and the Merkle root already available within the block header, we can verify the presence of transaction ‘a’ in this block.

From the above example, it is clear that to verify the presence of ‘a’, ‘a’ does not have to be revealed nor do ‘b’, ‘c’, and ‘d’ have to be revealed, only their hashes are sufficient. Therefore Merkle proof provides an efficient and simple method of verifying inclusivity, and is synonymous with “proof of inclusion”.

A sorted Merkle tree is a tree where all the data blocks are ordered using an ordering function. This ordering can be alphabetical, lexicographical, numerical, etc.

Advantages of Merkle Tree

• Efficient Verification

Merkle trees offer efficient verification of integrity and validity of data and significantly reduce the amount of memory required for verification. The proof of verification does not require a huge amount of data to be transmitted across the blockchain network.

This further enables the trustless transfer of cryptocurrency in the peer-to-peer, distributed system by quickly verifying transactions.

• Less Delay in Data Transfer

There is no delay in the transfer of data across the network. Merkle trees are extensively used in computations that maintain the functioning of cryptocurrencies.

• Less Disk Space

Merkle trees occupy less disk space when compared to other data structures.

• Unaltered Transfer of Data

Merkle root helps in making sure that the blocks sent across the network are whole and unaltered.

• Tampering Detection

Merkle tree gives an amazing advantage to miners to check whether any transactions have been tampered with.

Since the transactions are stored in a Merkle tree which stores the hash of each node in the upper parent node, any changes in the details of the transaction such as the amount to be debited or the address to whom the payment must be made, then the change will propagate to the hashes in upper levels and finally to the Merkle root.

• Time  Complexity

Comparing the time complexity of searching for a transaction in a block using a Merkle tree versus a linked list arrangement yields insightful results:

1. Merkle Tree Search: O(logn), where n is the number of transactions in a block.

2. Linked List Search: O(n), where n is the number of transactions in a block.

3. So the Merkle Tree search will be efficient.

Conclusion

In conclusion, Merkle trees are fundamental to the functionality and security of blockchain technology. By using cryptographic hash functions and hierarchical data structures, Merkle trees promote efficient data verification, tamper detection, and proof of membership within blockchain networks. Embracing Merkle trees ensures the integrity, scalability, and efficiency of distributed ledger systems in various applications.