About OFR Insight Sharing

OFR Insight Sharing is a weekly program session presented by Old Fashion Research, joined by other crypto practitioners of multiple notable institutions and media presses. Every week, researchers of OFR Fund will share their research results in the crypto industry for the past week. Recaps take a look back at the sharing sessions and expose a larger audience to the most discussed topics recently.

This week, we are pleased to feature Scott, Web3 Researcher of ResearchDAO, to share his insights and understandings on Zero-Knowledge Proof (ZKP).

Scott is a Master of Finance at Fudan University and a crypto enthusiast since 2016. He primarily served as a Semiconductor Analyst Intern and IoT Engineer and has been a CFA Level III Candidate. Follow Scott on Twitter @CryptoScott_ETH

____________________________________________________________________________

ZKP(Zero-Knowledge Proof) is currently a popular black technology, but its technical details are more difficult to understand. This article is to sort out the relevant data in the field of zero-knowledge proof and discuss the application in the industry, hoping to provide non-technical researchers with guidance on ZK research and helping them understand zero-knowledge proofs from the simple to the deep.

Understand ZKP from the story of Alice & Bob

This chapter is a summary of The Incredible Machine published by Aviv Zohar in 2017. It helps readers to understand the relevant characteristics of zero-knowledge proofs more intuitively from a comprehensive story.

Alice and Bob are both Sudoku lovers. One day, Alice said to Bob, "I designed a very difficult Sudoku. Would you like to challenge it?" Bob accepted the challenge, but he was unable to fill the blanks, so he questioned Alice that her design has no solution. In order to prove that the problem has a solution without revealing the answer itself, Alice thought of a way.

• The Commitment: Alice takes 81 (9x9) blank cards and puts them on the table, writes a number from 1-9 on each sheet, he turns Bob around and closes his eyes, then puts the 81 cards placed on the table according to the arrangement of the solution. The cards representing the solution are placed on the table with the numbers facing down; the cards representing the riddle are placed on the table with the numbers facing up.

• The Random Challenge: Bob randomly selects the row, or by the column, or by the 3x3 nine-square grid to test the solution. Then put the selected 9 cards away and put them individually in a bag. All cards were collected and placed in 9 bags. Alice then shook each bag, breaking the order of the cards inside. She returns the 9 bags to Bob.

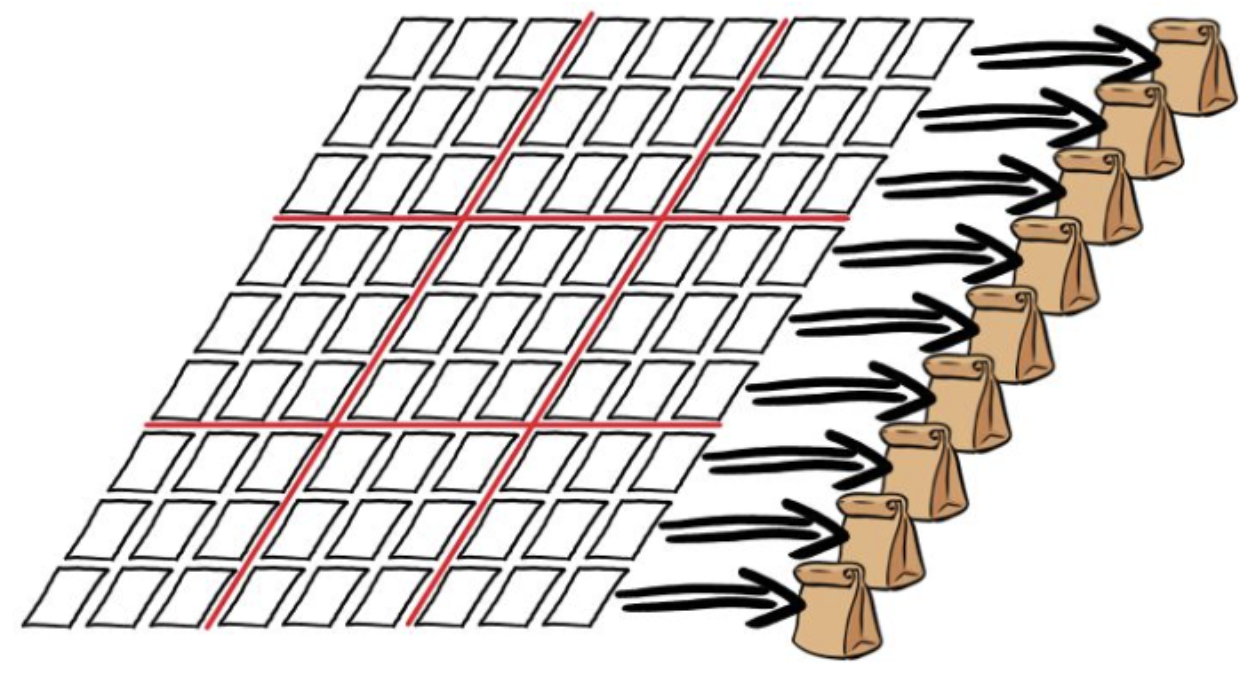
• Verification: Bob opens the bags and verifies that each bag contains number cards from 1 to 9

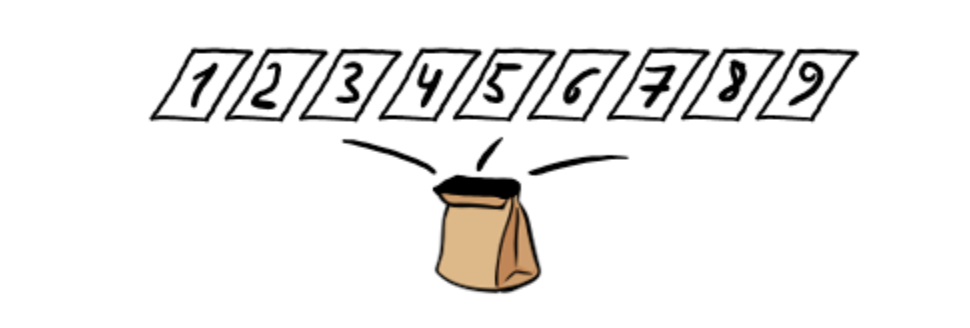
• Repeat: According to the rules of Sudoku, the numbers in each row and column of each nine-square grid will not be repeated. Only one random experiment is performed, and the probability that Alice does not lie is only 1/3. Repeat the experiment several times, and the result of each experiment will not be repeated. Repeating numbers proves that Alice really knows the solution to the problem.

• Non-Interactivity: Alice and Bob's selection arrangement is interactive, and there is a possibility that the two parties may join forces to deceive a third party. So Charlie designed a machine to select the row and column blocks to achieve the non-interaction of random experiments. Alice just puts the card on the conveyor belt, the machine will automatically choose to collect the card by row, column, or grid, put it in the bag to shuffle the order, and then send the bag through the conveyor belt.

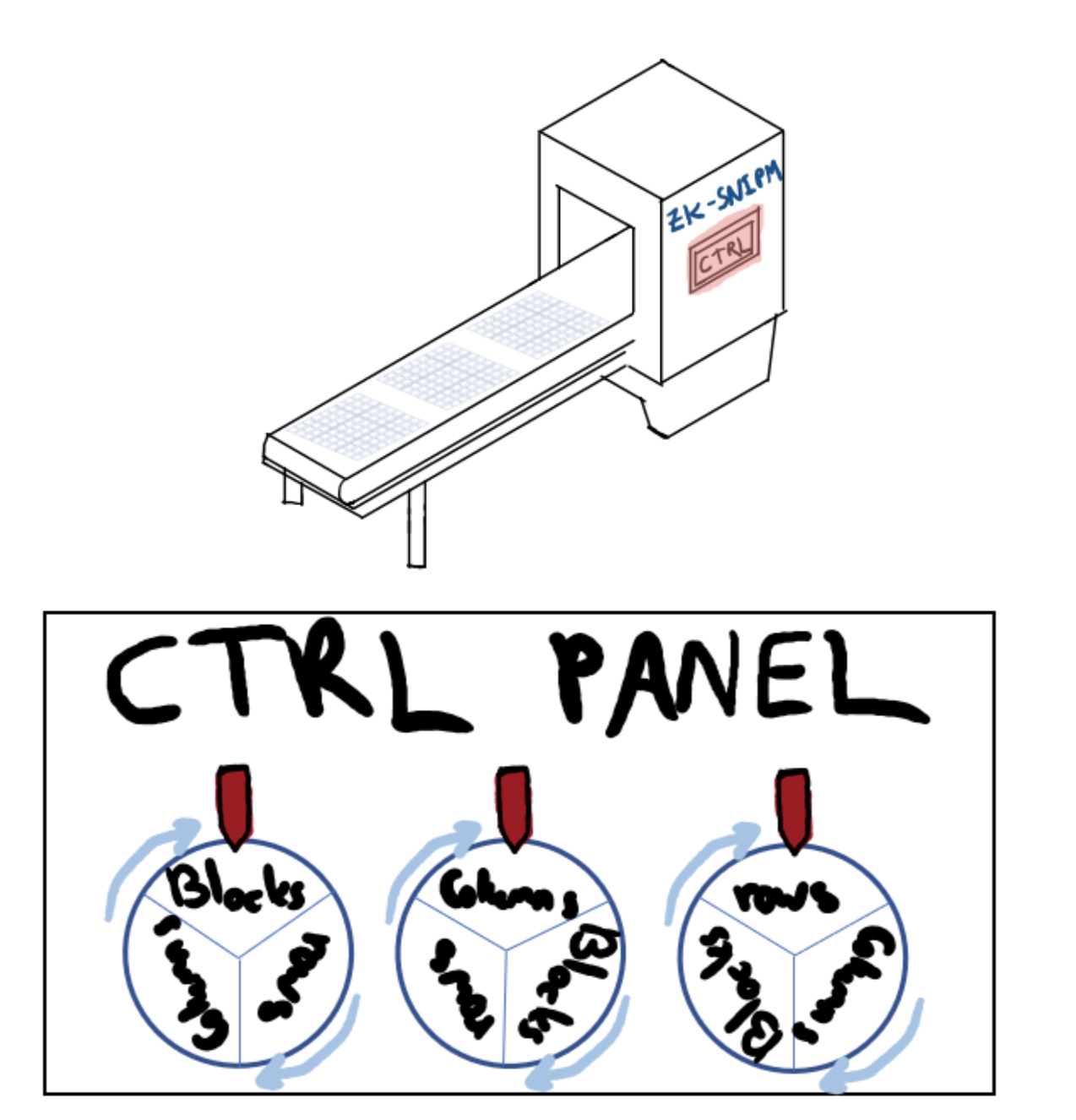
• Trusted Setup: The extraction order of row and column blocks is set by Charlie, so this machine cannot verify whether he can solve Sudoku or not. Others can also bribe Charlie to know the extraction order. Alice then proposes to have Charlie turn the control panel back on, and a multi-party set up the test sequence on the control panel. This process is called a "trusted setup ceremony". The machine is placed in a dark room, the first person enters the room and turns the dial to any random position, the second person and the third person add one and two cells down in the order randomly selected by the first person. In this way, it ensures that each dial will not be known to any of them. After this setup ceremony is completed, they will weld the control panel of the machine.

Such a machine can realize the three characteristics of zero-knowledge:

• Completeness - as long as the "statement" is correct, the prover can convince the verifier

• Reliability - if the "statement" is false, there is no way for a cheating prover to convince a verifier

• Zero knowledge - the interaction of the protocol only reveals whether the "statement" is correct and does not reveal other information other than public information

Understand ZKP from a mathematical perspective

This chapter is about the mathematical proof process of ZK-SNARK (the mainstream ZKP). It mainly refers to Quadratic Arithmetic Programs: from Zero to Hero published by Vitalik Buterin in 2016. From a mathematical point of view, it helps readers to further understand the implementation process of zero-knowledge proof.

Preliminary knowledge

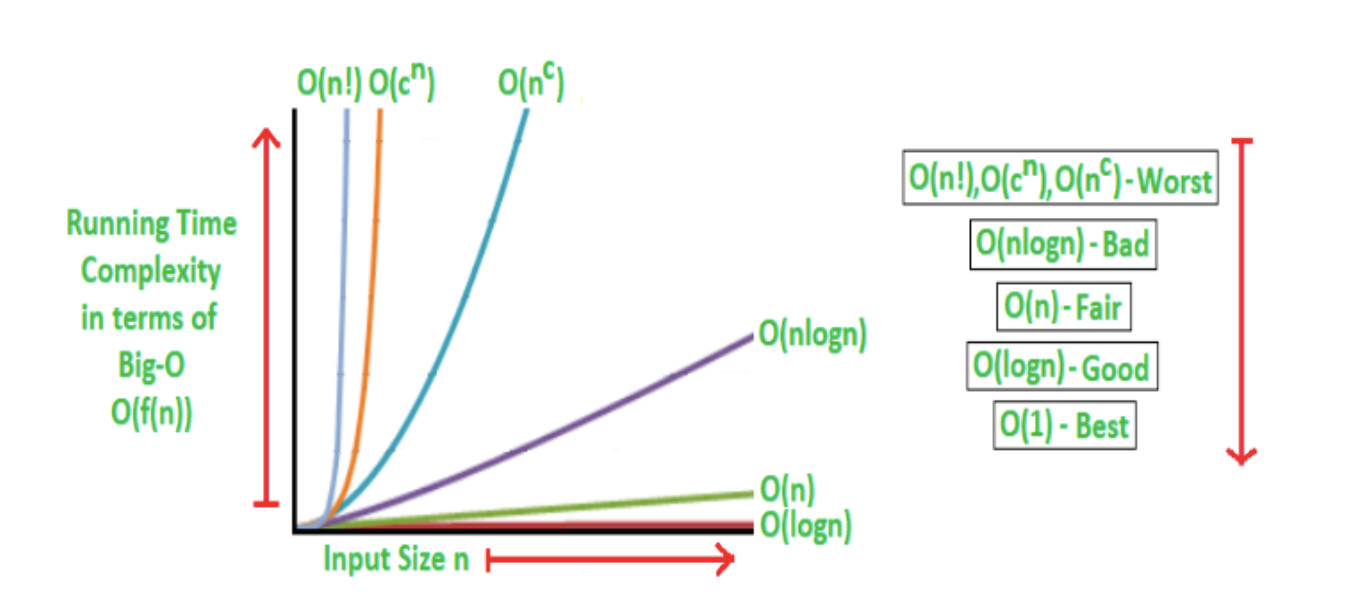
• Complexity

  • How fast the length of time the procedure takes grows as the problem scales up.

  • No matter how big the data is, the time it takes to process the program is always that much, we say that this program is very good and has O(1) time complexity, also known as constant-level complexity;

  • How big the data size becomes, and how long it takes, the time complexity of this program is O(n).

  • O(1), O(log(n)), O(n^c), etc. We call it polynomial level complexity.

  • O(c^n) and O(n!) type complexity, which is non-polynomial, and the complexity of which computers often cannot afford.

  • When we are solving a problem, the algorithm we choose usually needs to be polynomial-level complexity, and non-polynomial-level complexity requires too much time and often times out, unless the data size is very small.

• P problem and NP problem

  • P problem: a problem solvable in polynomial time, such as

    • Knowing the private key sk and the elliptic curve generator G, the public key pk = sk * G can be quickly calculated

    • Knowing the original image x and the hash function SHA256, you can quickly calculate the hash value Y = SHA256(x)

• NP problems: problems that cannot be solved in polynomial time (difficult to solve), but can be verified in polynomial time (easy to verify), such as:

  • Knowing the public key pk and the elliptic curve generator G, the private key sk cannot be calculated in polynomial time such that pk = sk*G

  • Knowing the hash value Y and the hash function SHA256, the preimage x cannot be calculated in polynomial time such that Y = SHA256(x)

• Polynomial

  • Polynomials have a very nice property that if we have two unequal polynomials of degree d, they will not intersect at more than d points. It is impossible for us to find two different curves, they will coincide in a certain area (they will only intersect at some points).

  • For example, to check whether two vectors of length 1000 (the information provided by the prover and the correct information) are equal, be sure to check 1000 times, and two polynomials of 1000th degree have at most 1000 points the same, in a large take for a range of values, such as 1 to 100 million, the probability that two different polynomials are the same at the same point is only 1 in 1 million. Checking if two polynomials are equal is much faster than checking if two vectors of equal size are equal.

  • (Ax, s) * (Bx, s) - (Cx, s) is a quadratic algorithm polynomial, referred to as a QAP polynomial (Ax, Bx, Cx are d-order polynomials, s is a d-order vector, and QAP is a 2d-order polynomial) . a1,a2,…,an is the solution of the QAP polynomial equal to 0, let Z(x)=(x-a1)*(x-a2)*…*(x-an), then the QAP polynomial can be calculated by Z(x) Divisible.

  • If the vector s is not known, it takes exponential time to violently search for the vector s, so that the constructed QAP polynomial can divide Z(x).

  • Divisibility relation of QAP polynomials, constituting NP problems.

• Arithmetic circuits

  • In terms of writing programs with circuits, it is relatively mature. For example, CPUs, various chips, embedded devices, ASIC mining machines, etc., are all circuit designs. At the same time, the structure of the circuit is simple enough not to cause too much trouble to construct the ZKP. It's just that ZKP commonly uses arithmetic circuits (left), and Boolean circuits are common in hardware (right).

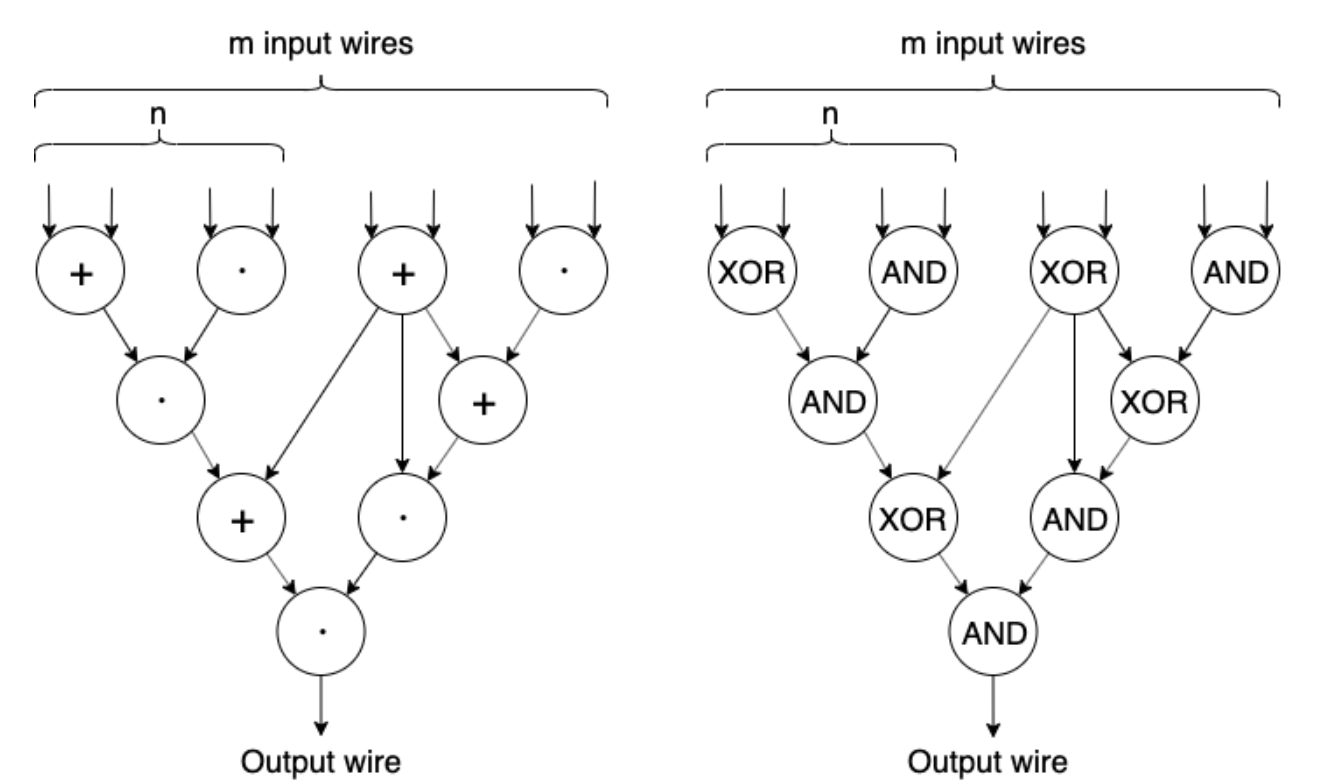
• Codes for polynomial-time operational relationships can be represented by arithmetic circuits. The arithmetic circuit consists of addition gates and multiplication gates.

• Continuously smooth functions can be infinitely approximated by Taylor expansion, which consists of addition and subtraction and exponentiation, and the power function consists of multiplication. Bitwise operations such as AND and XOR are not smooth and are more difficult to represent by addition and multiplication.

• Basic knowledge of linear algebra

  • Vector inner product operation

• As shown in the figure on the left, if the input is known and the verifier wants to verify whether the result given by the prover is correct, the final result can be compared with the output through the value of each node in the arithmetic circuit. However, this process cannot achieve simplicity, that is, the calculation time used by the prover and the verifier to draw a conclusion is the same, so the value in the operation process can be used as an unknown variable and verified by zero-knowledge proof. To achieve the simplicity of the verification process; as shown in the figure on the right, in order to maintain the privacy of part of the input, the prover can use zero-knowledge proof technology to make the prover believe that the prover knows the correct solution.

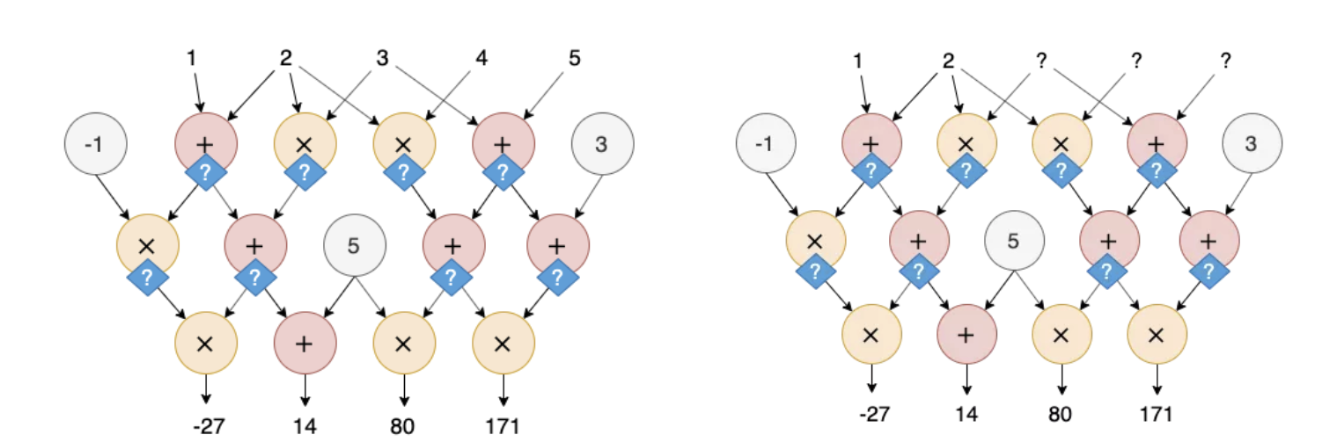
• The information known to the Verifier is Statement (shown in green in the figure below), and the knowledge that the Prover knows but the Verifier does not know is Witness (shown in blue in the figure below).

**

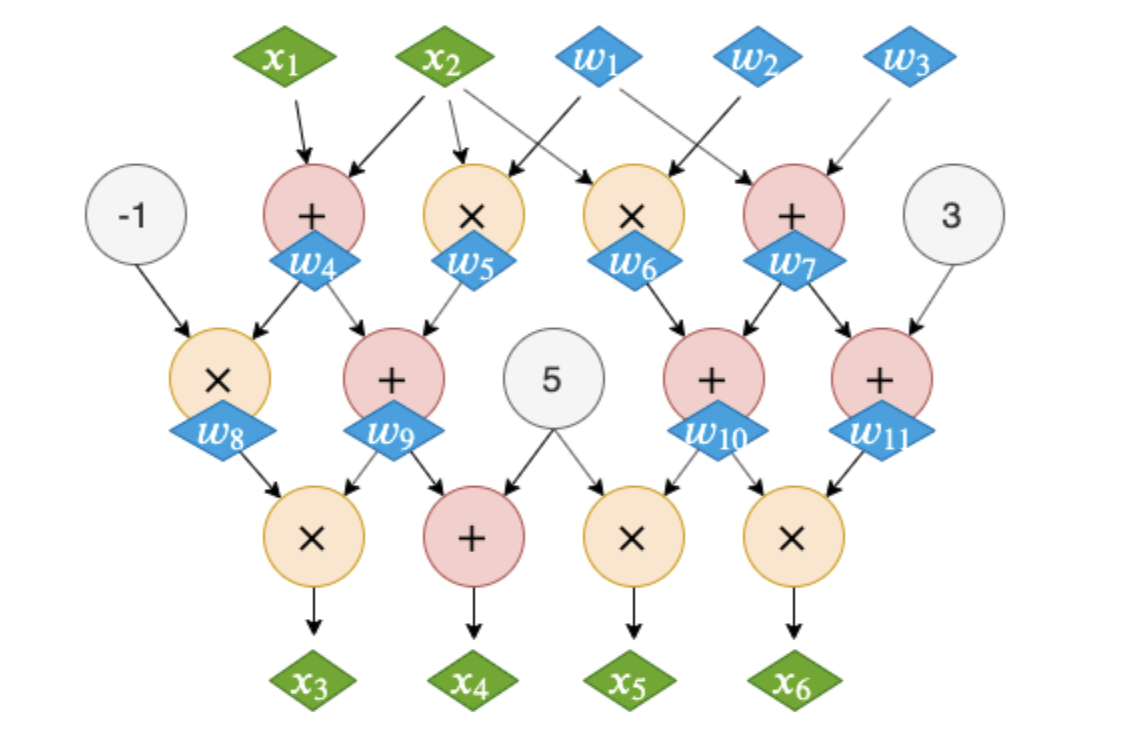
The mathematical proof process**

1. In order to achieve simplicity or zero-knowledge, the algorithm needs to be converted into an NP problem (easy to verify, difficult to solve)

2. The answer known by the verifier and the information data contained in the correct answer can be represented by a vector. To determine whether two vectors are equal, a vector length operation is required. For example, to determine whether two vectors of length 100 are equal, 100 comparisons are required. conclusions can be drawn later. Conciseness and zero knowledge are not achieved.

3. Judging whether two polynomials are equal is easier than judging whether two vectors are equal, because two different n-order polynomials are at most compared to n points, as long as the range is large enough, the point where the two functions intersect will be collided. The probability is extremely low, an unlikely event. For example, two different 100th-order polynomial functions have at most 100 identical points. If the value range of x is set to [-1,000,000, 1,000,000], a random point is selected so that the probability of the intersection of the two polynomials is 100/ 2,000,000=1/20,000, if two points are taken uniformly so that the probability of two polynomials intersecting is (1/20,000)*(1/20,000), it is an impossible event.

4. Converting the problem of verifying whether two vectors are equal to verifying whether two polynomials are equal can greatly reduce the computational complexity. SNARK converts the vector comparison problem into a natural NP problem that divides the target polynomial by the QAP polynomial as a verification method.

5. In order to construct the QAP polynomial, the program needs to be converted into an arithmetic circuit to construct the R1CS.

6. SNARK proof process: the program is transformed into a polynomial time operation relation -> R1CS -> QAP -> QAP divisible relation -> elliptic curve discrete logarithm.

ZK-SNARKs and ZK-STARKs

The current mainstream ZKPs are zkSNARK and zkSTARK. SNARK, STARK, and ZKP are all proof systems. The intersection of SNARK and ZKP is called zkSNARK, and the intersection of STARK and ZKP is called zkSTARK.

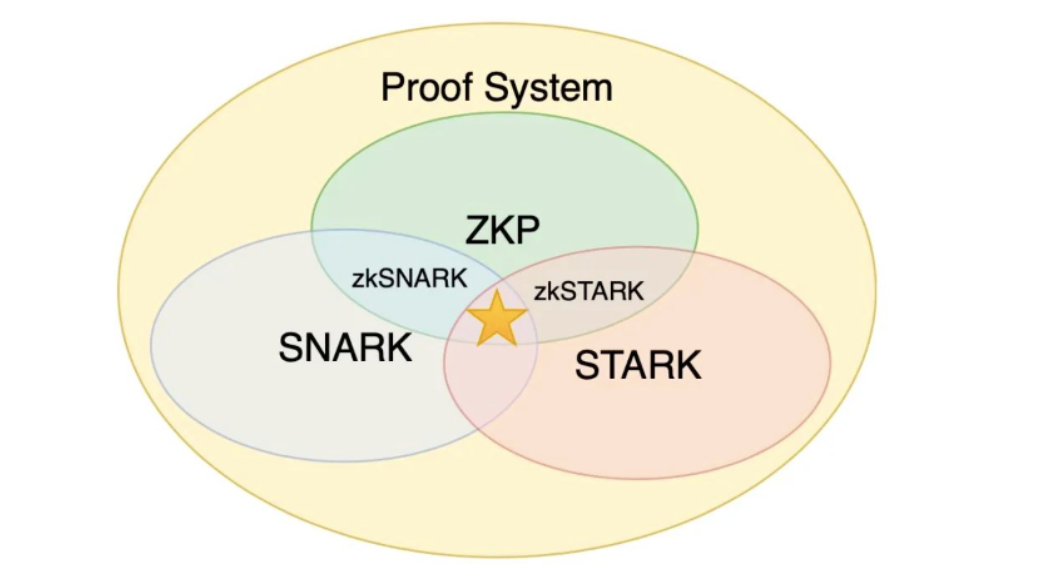
The meanings of SNARK and STARK

SNARK

• S: Succinctness. Prover and Verifier implement this proof system, which saves communication bandwidth compared to Prover sending w directly to Verifier. Occasionally, succinctness may also require Verifier to be less computationally expensive in the proof system than to verify w. In summary, succinctness requires proving that the system has an advantage in terms of efficiency.

• N: Non-Interactivity means that the entire interaction of the proof system is only a message sent by the Prover to the Verifier, which is called a proof. Non-interactivity can bring many conveniences and bring more application scenarios to the proof system. For example, in a blockchain system, a non-interactive zero-knowledge proof can be attached to a transaction for anyone to check at any time, without requiring the author of the transaction to interact with the validator online at any time. Any NP language naturally has a non-interactive proof protocol, that is, the Prover sends the proof directly to the Verifier, and the proof is a knowledge proof.

ARK: Argument of Knowledge. If the Prover is required to "know" some information in order for the Verifier to pass verification, the system is called Proof of Knowledge. Proof of Knowledge can be seen as an enhanced version of reliability. The computational version of a Proof of Knowledge is called an Argument of Knowledge.STARK

• S: Scalability, which requires the Prover complexity to be at most Quasi-linear, ie O(n log n), based on succinctness. The proof time has a quasi-linear relationship with the complexity of the proof content, while the verification time has a multi-logarithmic relationship with it. Therefore, when the complexity of the proof content increases significantly, although the off-chain proof time also increases quasi-linearly, the on-chain verification time does not increase much.

• T: Transparent, STARK does not require a trusted third-party setup.

• ARK: Argument of Knowledge. 

Similarities and differences between SNARK and STARK

STARK and SNARK are only one word apart, but there are many differences. Let's compare these two concepts.

Common ground:

• Both are arguments of knowledge (ARK), i.e. reliability in the computational sense only, and proofs are knowledgeable

the difference:

• SNARK's "S" is Succinctness, while STARK's "S" is Scalability, which requires Prover complexity to be at most quasi-linear (Quasi- linear), which is O(n log n).

• Transparency: STARK does not require a trusted third-party setup, so it is resistant to quantum computing.

• Non-Interactivity: SNARKs must be non-interactive, while STARKs do not have this limitation. It can be seen that the only limitation of SNARK over STARK is non-interactivity. Nevertheless, STARKs can generally be transformed into non-interactive proofs, and the result of the transformation must be a SNARK. In this sense, STARKs can be thought of as a subset of SNARKs.

• Most of the current zkSNARKs are based on circuit models, STARKs are based on RAM models, and the construction of RAM models is extremely complex.

• The size of cryptographic proofs generated by zk-STARKs is much larger. Additionally, Ethereum has precompiled for specific zk-SNARKs, so the gas cost of validating cryptographic proofs for zk-SNARKs is lower than for zk-STARKs.

ZKP Applications

ZKP is mainly used in the two directions of expansion and privacy, and the privacy direction includes privacy applications and privacy public chains built on Layer1 or Layer2. Before DeFi broke out, ZKP was mainly used in the direction of privacy. After the outbreak of DeFi, the high gas fee was the biggest obstacle to the large-scale use of Ethereum. Therefore, everyone began to turn their attention to Layer2 expansion, and in the Layer2 scheme, zk-Rollup has the best performance in terms of security and gas cost savings.

Layer 2 expansion

Before discussing the Layer 2 expansion, let's have a general understanding of the gas composition of Ethereum.

Layer 1 Gas Composition

The calculation method of gas fee on Ethereum is gas price (gasPrice) * gas cost (gasUsed).

• The gas price (gasPrice) is a quotation method, you can choose the quotation level by yourself, and the gas price (gasPrice) is related to the transaction speed. The gas price (gasPrice) has a positive correlation with the priority of the transaction, when the transaction demand of the same level of complexity and the higher the gas price (gasPrice), the miners will be more inclined to give priority to processing, and the transaction speed will be faster.

• The gas cost (gasUsed) is positively related to the complexity of the transaction. The higher the transaction complexity, the higher the gas cost (gasUsed); otherwise, the lower it is. For example, if you perform transfer operations and leverage operations separately, generally speaking, the cost of the former will be lower than that of the latter, because leverage operations are more complicated.

Rollup transfers the transactions that need to be calculated on the mainnet to off-chain, and then feeds back the calculated results to the mainnet, thereby reducing the complexity of transactions and reducing gas costs; the solution of ETH2.0 is to reduce the unit price of gas fuel on the mainnet, thereby reducing the gas cost.

Optimistic Rollup vs ZK Rollup

The Layer 2 expansion scheme can be divided according to the data storage method and the proof system. The specific division method is shown in the following figure. The current mainstream solutions are Optimistic Rollup and ZK Rollup.

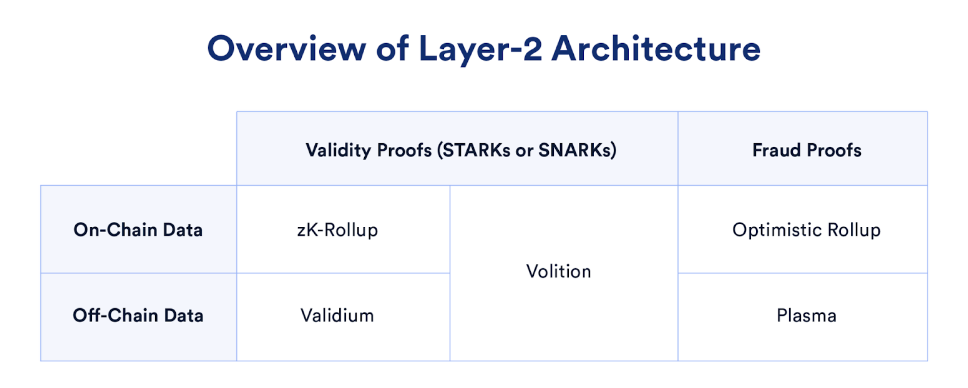
• Optimistic Rollup

  • The method of interactive fraud proof is used to ensure security, that is, when the calculation result of Layer 2 is returned to Layer 1, when the Verifier believes that the result may be fraudulent, the Verifier initiates a challenge, and then the mainnet freezes the assets, conduct transaction data and record verification, and finally prove whether it is a real transaction or a fraudulent transaction. When no validator doubts this result, the mainnet defaults that these results are true.

  • Advantages: good compatibility;

  • Disadvantages: low security (there is no fundamental guarantee of the control of assets, that is, the security of assets is threatened); assets will be frozen; the withdrawal cycle is long.

• ZK Rollup

  • Pack a large number of transactions into a Rollup block and generate a compact proof of the block off-chain. Subsequently, the smart contract on Layer 1 can directly apply the new state by simply verifying this proof, without re-executing these transactions. This saves an order of magnitude in gas costs, since the cost of proof verification is much lower than the computational cost of re-execution. Another benefit is that storage space can be saved through data compression (i.e., only a minimal amount of data is stored on-chain for verification).

  • Advantages: high security, short withdrawal period, low gas fee

  • Disadvantage: poor compatibility

Privacy

Privacy applications

• Tornado.Cash

The transaction records on Ethereum are public, you can see all the historical transaction records of an address on Etherscan, and know the asset balance of each address. In traditional financial payment, people are often reluctant to let others know how much money is in their account, and they are also reluctant to let anyone at random check their own transaction records. ZK technology can solve this problem very well.

Tornado.Cash, as the hottest decentralized privacy solution on the Ethereum network, uses zk-SNARKs technology to break the on-chain link between the addresses of depositors and withdrawers, achieves transaction confidentiality, and protects user privacy. Anonymous token transactions are realized. Simply put, it is a contract. When you want to transfer tokens anonymously, you throw a certain amount of coins into the contract (Deposit). At this time, you will get a note. Note is a string of characters. The person with this string can withdraw (Withdraw) the token just passed into the contract. Holding a note means having the right to withdraw money, so once the note is known to others, others can withdraw the money.

• Dark Forest

At present, GameFi basically only has assets on-chain, and the asset value of the game depends to a large extent on the game itself. After the centralized operation of the game is closed, the value of the assets on-chain no longer exists. A game that has on-chain assets only is not decentralized enough. A game that deploys the entire game on the blockchain can be called a true decentralized game.

The universe is like a dark forest, and the civilizations that exist in the universe are like hunters with guns. If a civilization is the first to discover another civilization in the universe, then it will attack like a hunter shooting a prey, Eventually a civilization is always wiped out. Due to the existence of this law, every civilization is very careful in its activities in the universe, but it is inevitable that some civilizations will expose their whereabouts and be attacked by other civilizations.

Dark Forest is a real-time strategy game and the first fully on-chain game to run on the Gnosis chain. The movement and capture of planets is the strategic focus of the entire game. Since it is a mobile attack, each planet has a coordinate. In order to increase the strategic experience of the game, the exact coordinates of the planet are not disclosed. It's a bit like in the vast universe, you can only observe (enumerate) the limited space around (hash collision) to find other planets. In order to prove the correct movement of the planet without disclosing the coordinates of the planet, zero-knowledge proof technology was introduced.

Privacy public blockchains

• Zcash

Zcash was born on November 9, 2011, its full name is Zero Cash, or ZEC for short. Most of Zcash’s code is very similar to Bitcoin, with a total of 21 million tokens, but it further improves the lack of Bitcoin’s anonymity function. Zcash is the first blockchain system to use the Zk-SNARK zero-knowledge proof mechanism to completely solve the problem of transactions being tracked and exposing user privacy. Zcash transactions automatically hide the sender, receiver and amount of all transactions on the blockchain. Only those with the viewing key can see the contents of the transaction. Users have full control, and they can choose to provide viewing keys to others. Currently, Zcash transactions are divided into two categories: transparent addresses (starting with "t") and hidden addresses (starting with "z"). If the user wishes to verify the details of the hidden address, a special access key must be shared with the relevant parties. Users can also "selectively disclose," which also comes with an encrypted memo field that allows institutions to securely attach sensitive data to transactions and make that information visible to authorized parties.

• Iron Fish

Iron Fish is committed to providing strong privacy guarantees for every transaction. Transaction information, mining information, and wallet information are all hidden, and cannot be viewed by any second party except the private key owner. To achieve this, Iron Fish has built a new PoW network that uses zk-SNARKs and the Sapling protocol to provide the highest level of privacy protection for every on-chain transaction.

One of the highlights of Iron Fish is that the network wants to preserve privacy without compromising the accessibility of on-chain transactions, so Iron Fish equips each on-chain address with an additional view key. The address holder can grant others read-only access through this key.

Currently, Iron Fish is still in the testnet stage and has launched an incentive program. Active participants can earn corresponding points through various contributions, and these points will be exchanged for mainnet tokens when the mainnet is released in the future.

• Mina

Mina is a lightweight public chain. Through recursive zero-knowledge proof, the size of the blockchain is maintained at about 22 KB, which allows nodes to participate with low requirement of hardware conditions, even for mobile terminals with relatively weak computing power, similar to mobile phones, tablet computers, etc., can also verify the Mina network synchronously. The requirements for running a node is lower, the nodes are more distributed, and an ecosystem that can protect data privacy is built around zero-knowledge proof.

Recursive zero-knowledge proof means: at each block production, the block is compressed into a single proof using zk-SNARK technology, and each new SNARK proof contains the past SNARK proof, and the node only needs to detect the proof. This eliminates the need to examine the entire transaction history, and the proofs can be recursively combined to achieve constant block size.

Compatibility - ZK EVM

The Ethereum Virtual Machine (EVM) is blockchain-based open-source software that allows developers to create decentralized applications. It is the global virtual computer that records the state of every smart contract that the Ethereum network stores and reaches consensus, and Solidity is its programming language. EVM was the first software to provide developers with smart contract capabilities and has grown into a thriving ecosystem with valuable developer network effects that extend beyond the Ethereum blockchain itself.

A protocol is EVM compatible if its smart contracts can be executed on the EVM, which means that the protocol's contracts must either be written in Solidity, or be able to compile its contract code into words that can run on the EVM section code. If a new public chain or Layer2 wants to rapidly expand its ecosystem, EVM compatibility is essential, and applications written in Solidity on Ethereum can be quickly deployed to their own chains. The Solidity language has many ZK-Unfriendly syntaxes, which makes the implementation of ZK-EVM face great challenges. Which protocol can achieve better EVM compatibility will achieve network effects faster.

• Solidity source code → compiler → EVM executable bytecode → EVM → EVM interpreter → machine executable binary file → program execution.

• Solidity source code → compiler → zkEVM executable bytecode → zkEVM → zkEVM interpreter → machine executable binary file → program execution.

• Non-Solidity source code → compiler → EVM executable bytecode → EVM → EVM interpreter → machine executable binary file → program execution.

This chapter is a generalization and summary of The different types of ZK-EVMs published by Vitalik in 2022 and zkEVM published by Ye Zhang in 2022. From the perspective of the classification and technical evolution of ZK-EVM, it helps readers better understand ZK-EVM development status.

Design challenges

• First, EVM has limited support for elliptic curves. Currently, EVM only supports BN254 pairing. EVM has difficulty implementing proof recursion due to no direct support for cyclic elliptic curves. With this setup, it is also difficult for us to use other proprietary protocols. The verification algorithm must be EVM friendly.

• Second, the word size of the EVM is 256 bits. The EVM operates on 256-bit integers (like most common virtual machines that operate on 32-64-bit integers), and zero-knowledge proofs operate "naturally" on prime fields. Doing "mismatch domain arithmetic" in a circuit requires range proofs, which in turn add about 100 constraints to each EVM operation. This increases the EVM circuit size by two orders of magnitude.

• Third, EVM has many special opcodes. Unlike traditional virtual machines, EVM has many special opcodes, such as CALL, and error types related to the execution environment and gas. This brings new challenges to circuit design.

• Fourth, EVM is a stack-based virtual machine. The SyncVM (zkSync) and Cairo (Starkware) architectures define their own IR/AIR in a register-based model. They built a specialized compiler to compile smart contract code into a new zero-knowledge proof-friendly IR. This method is language compatible, not native EVM compatible. Whether it's proving a stack-based model, or directly supporting native toolchains, it becomes more difficult.

• Fifth, the Ethereum storage layout brings high costs. The Ethereum storage layout is highly dependent on Keccak and a giant MPT4. Neither is zero-knowledge proof-friendly and incurs high proof costs. For example, the circuit size of Keccak hash is 1000 times larger than that of Poseidon hash. However, if you replace the Keccak hash with another hash, it will introduce some compatibility issues with the existing Ethereum infrastructure.

• Sixth, machine-based proofs come with high costs. Even if you can handle all the above problems properly, you still need to find an efficient way to combine them to get a complete EVM circuit. As I mentioned in the previous section, even a simple opcode like add can potentially cost you the entire EVM circuit.

Categories

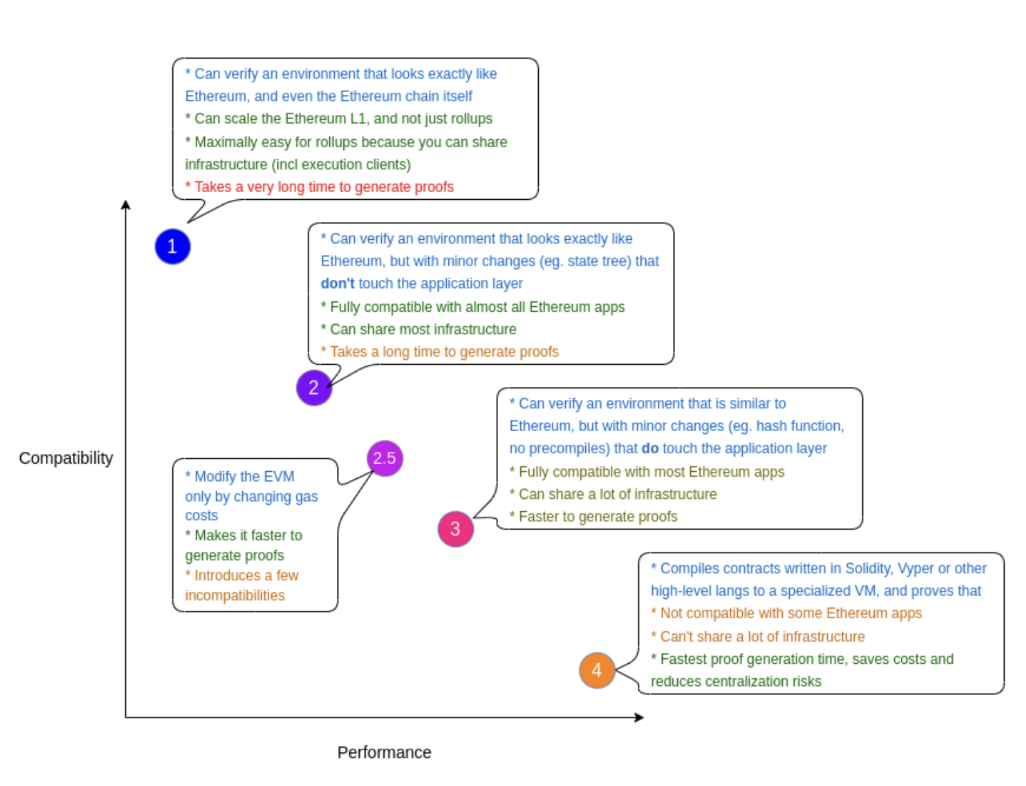
• Type 1 (exactly Ethereum equivalent)

Strive to be completely and uncompromisingly equivalent to Ethereum. Proofs are generated without changing any part of the Ethereum system.

Advantages: Perfectly compatible, this type of ZK-EVM is what we need most, making Ethereum layer 1 itself more scalable, and ideal for rollups as it allows rollups to use a lot of infrastructure. (The consensus level can also be implemented with ZK)

Disadvantages: Proving time is long. Ethereum was not originally designed around ZK friendliness, so many parts of the Ethereum protocol require a lot of computation to be ZK proofs. Type 1 is designed to replicate Ethereum exactly, so it cannot mitigate these inefficiencies.

Builders: privacy-scaling-explorations

• Type 2 (exactly EVM equivalent)

Type 2 ZK-EVM seeks to be fully equivalent to EVM, but not fully equivalent to Ethereum. That is, they look exactly like Ethereum "from the inside", but they have some differences on the outside, especially in data structures like block structure and state tree.

Pros: Perfect equivalence at the VM level, you won't be able to execute clients using Ethereum as-is, but you can use them with some modifications, and you can still use the EVM debugging tools and most other developer bases facilities.

Cons: There are improvements but still need to provide faster proof times than Type 1, mostly by removing parts of the Ethereum stack that rely on unnecessarily complex and ZK-unfriendly cryptography, but they don't solve everything .

Builders: Scroll's ZK-EVM project is heading towards Type 2 ZK-EVM, as is Polygon Hermez. That said, neither project is complete yet. In particular, many of the more complex precompiled are not implemented yet. So both projects are better considered Type 3 at the moment.

• Type 2.5 (EVM equivalent, except gas cost)

One way to significantly improve worst-case prover time is to greatly increase the gas cost of certain operations in the EVM that are difficult to ZK proofs. Changing the gas cost may reduce developer tool compatibility and break some applications, but it is generally considered less risky than a "deeper" EVM change.

Benefit: Speeds up proof time

Disadvantage: Partial incompatibility

• Type 3 (almost EVM equivalent)

Type 3 ZK-EVM is nearly equivalent to EVM, but makes some sacrifices in exact equivalence to further reduce verification time and make EVM easier to develop, possibly removing some that are extremely difficult to implement in ZK-EVM implementations function.

Advantages: Easier to build, faster verification time

Cons: More incompatibilities. These types of ZK-EVMs aim to be compatible with most applications and require minimal rewriting of the rest. That said, there will be some applications that will need to be rewritten.

Builders: Scroll and Polygon are both Type 3 in their current form, although they are expected to improve compatibility over time. Polygon uses some different internal logic to do it. Type 3 is just a transitional phase until the complex work of adding precompiles is done and the project can move to Type 2.5.

• Type 4 (high-level language equivalent)

Type 4 works by taking smart contract source code written in a high-level language (such as Solidity, Vyper, or an intermediate language that both can compile) and compiling it into some language explicitly designed to be ZK-SNARK friendly.

Pros: Very fast verification time by not doing ZK proofs for all the different parts of each EVM execution step, and starting directly from higher-level code, you can avoid a lot of costs.

Cons: more incompatibilities

Builders: ZKSync is a Type 4 system, although it may increase compatibility with EVM bytecode over time. Nethermind's Warp project is building a compiler from Solidity to Starkware's Cairo that will turn StarkNet into a de facto Type 4 system.

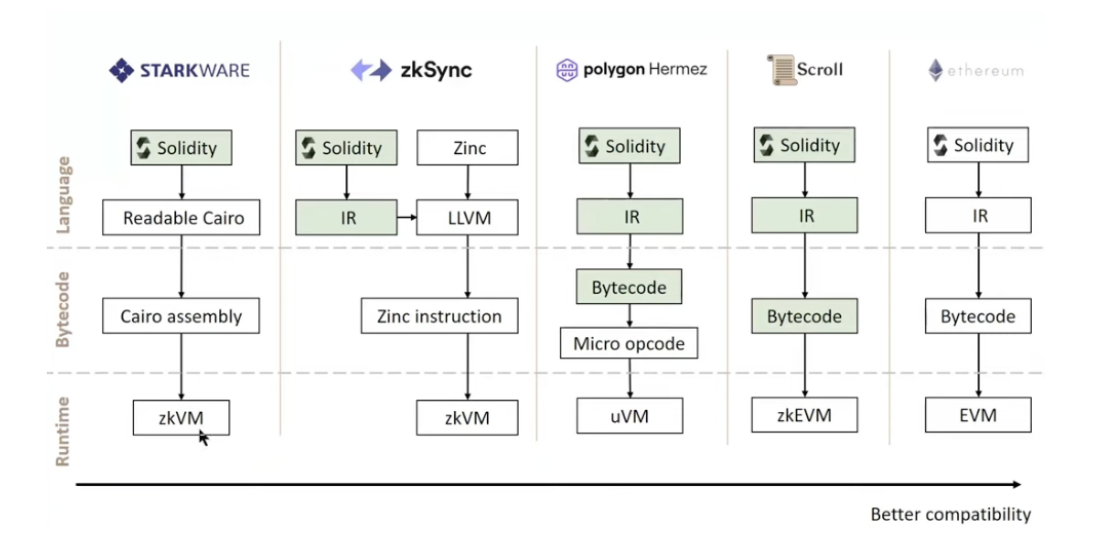
The future of different ZK-EVM types is not about which one is "better" or "worse". Instead, they are trade-offs that are spatially different: lower-numbered types are more compatible with existing infrastructure, but slower; and higher-numbered types are less compatible with existing infrastructure, but faster.

It can be seen that in order to achieve better compatibility, not only the ZK project party needs to work hard, but also the improvement of Ethereum itself and the development of hardware.

Possibilities of zkEVM Implementation

• Use of polynomial commitment. For the past few years, most compact zero-knowledge proof protocols have used R1CS, with PCP queries encoded into an application-specific trusted setup. This tends to increase the size of the circuit, making many custom optimizations impossible because each constraint must be of degree 2 (bilinear pairing allows only one exponential multiplication computation). With a polynomial commitment scheme, you can raise your constraints to any order via a universal setup or even a transparent setup, greatly increasing the flexibility of backend selection.

• Lookup table parameters and appearance of custom widgets. Another important optimization is the use of lookup tables. This optimization was first proposed in Arya and then implemented in Plookup. For zero-knowledge proof-unfriendly primitives (ie, bitwise operations like AND and XOR), lookup tables can save a lot of work. Custom widgets can efficiently implement higher-order constraints. TurboPlonk and UltraPlonk define an elegant program syntax that reduces the difficulty of using lookup tables and defining custom widgets. This goes a long way towards reducing the cost of the EVM circuit.

• Recursive proofs are getting more and more feasible. In the past, recursive proofs were expensive because they relied on special pair-friendly cyclic elliptic curves (i.e., MNT-curve-based structures). This incurs a high computational cost. However, a growing number of techniques enable recursive proofs without sacrificing efficiency. For example, Halo does not require pair-friendly curves and can also use a special inner product parameter to amortize recursion costs. Aztec demonstrated proofs that can directly aggregate existing protocols (lookup tables can reduce the cost of non-native field operations, thereby reducing the size of verification circuits). The same circuit scale can now achieve more functions.

• Hardware industry is accelerating and improving proof efficiency. As far as we know, we have built the fastest GPU and ASIC/FPGA accelerators for the proof program. Our paper on ASIC proof procedures was accepted this year by ISCA, the top academic computer conference. Our GPU prover is approximately 5 to 10 times faster than Filecoin's implementation, which greatly improves the computational efficiency of the Prover.

Conclusion

Before DeFi broke out, ZKP was mainly used in the direction of privacy. After the outbreak of DeFi, the high gas fee was the biggest obstacle to the large-scale use of Ethereum. Therefore, everyone began to turn their attention to Layer2 expansion, and in the Layer2 scheme, zk-Rollup has the best performance in terms of security and gas cost savings. The reason that hinders the large-scale outbreak of zk-Rollup is that due to its poor compatibility, many Layer 1 protocols need to be modified to deploy zk-Rollup. With the development of zk-EVM, this problem will be solved. The combination of ZK-Rollup and ETH greatly reduces the Gas fee while ensuring security, further hindering the development of Alt Layer1. At that time, Ethereum will further realize its vision of becoming a global settlement layer.

Discussions about the Future of the ZK Industry

• ZK Rollup P.K. Optimistic Rollup

• ETH + ZK Rollup P.K. Alt Layer 1

• The estimate market potential and commercial value of ZK Rollup

• Is it necessary to build an entire privacy chain?

• Other future applications

____________________________________________________________________________

Special thanks to Scott for presenting the content. Neither OFR Insight Sharing provides financial advice, nor researchers represent the final statement of OFR Fund.

ALL RIGHTS RESERVED TO Old Fashion Research

About Old Fashion Research

Old Fashion Research (OFR) is a multi-strategy blockchain investment fund founded in late 2021 by former executive and investment teams from the leading cryptocurrency exchange in the world.

OFR adopts a multi-strategy approach to capture the underlying value of Web3.0 and to build a full-cycle ecosystem to support new-generation crypto native entrepreneurs. OFR incubates promising startups, follows up with traditional venture capital investment and scaling support, and finally supports the projects if they wish to exit through a merger or acquisition.

**
Follow us Website | Twitter | Community | Mirror**