Huge thanks to Cat McGee for serving as my sounding board while I navigated through these intricate ideas. You've been an incredible support. And Raza, you're awesome. Your readiness to assist and your generosity with resources are deeply appreciated.

This week, I wanted to build a token transfer dapp to demonstrate how to send assets from a Layer 2 (L2) to a Layer 1 (L1). I would compare an optimistic rollup with a zero knowledge (ZK) rollup but, as I was thinking about it more, it dawned on me that I didn’t actually know how I would go about doing that.

Was it as simple as changing the RPC endpoints as when working with an optimistic rollup? Could I still write a contract in Solidity? And wtf is the zkEVM?

Twenty minutes later, I found myself in the ZK rabbit hole. I'm still in it, so this is going to be the first installment in a series on ZK rollup articles.

This guide is unfinished, so you might finish reading and think that we missed a lot of principles and concepts, and you would be right. The goal of this guide is not to be an encyclopedia of ZK rollups, but rather to serve as a stepping stone, capturing the essentials as I traverse the learning curve alongside you.

This series could include three articles, or possibly ten.

We’ll see how deep I dig.

In this first piece, we'll be getting our feet wet with ZK terminology, exploring ZK rollups, and delving into ZK proofs.

Terminology

Before getting into the weeds, let’s cover some basic ZK terms.

Zero Knowledge (ZK): In cryptography, it's a concept where one party can prove to another party that they know a specific piece of information without revealing what that information is.

Zero Knowledge Proof (ZK Proof): This is the actual output by which zero knowledge is conveyed—you might think of zero knowledge as the concept and the zero knowledge proof as the outcome of that concept.

Prover: This entity attempts to convince another entity that a particular statement is true. The prover can be an individual or a system.

Commitment: A cryptographic technique to securely 'seal' a secret, which, when 'unsealed', allows verification of the original secret without prior disclosure.

Witness: This is the confidential information that enables the prover to generate a proof about a statement without revealing the witness itself.

Real-World Example

Imagine Alex needs to apply for a loan. The bank must verify that Alex has a good credit score without actually seeing it. Here’s how it goes:

Prover (Alex): Alex needs to convince the bank that her credit score is good without disclosing the exact figure.

Witness: This is Alex's actual credit score—the secret information she doesn't want to disclose.

Zero Knowledge Proof: Alex uses the witness to create a ZK proof, essentially asserting, "I can confirm my credit score meets the required level, but I won't reveal the exact score." The ZK proof is reliable enough for the bank to trust without seeing the actual score.

Commitment: Alex applies a cryptographic method to "seal" her credit score, much like placing it in a tamper-proof envelope. The bank can't see the score but can use this 'envelope' to verify its validity later, if necessary.

Verifier (Bank): The bank needs to be sure Alex's score surpasses a specific threshold without knowing the precise score, just that it is above the minimum.

Alex provides the bank with a commitment, which the bank can check to confirm whether his score meets their standards. The bank doesn't need to see the score itself—just that it satisfies their criteria.

Congratulations, you've just grasped the basics of how ZK proofs function.

Introduction to ZK Rollups

Definition of a ZK Rollup

A ZK rollup is a kind of L2 scaling solution that builds upon a L1 blockchain, such as Ethereum. Its purpose is to reduce the computational workload on the L1, thereby lowering gas fees and making transactions cheaper by eliminating the processing step involved in executing smart contracts and ultimately posting them onto Mainnet (Ethereum).

How ZK Rollups Work

When a smart contract is deployed on a L2, it operates on a network that acts like a L1. This is where transactions are processed and the current state of the system is updated, all taking place off-chain.

After the transactions have been processed by the sequencer, the sequencer generates the blocks. Multiple blocks are consolidated and committed on L1.

Different L2s have slightly different capacities, so the volume of transactions will slightly vary.

Next, a prover is responsible for taking this collective data structure (the batch), and generates what's known as a validity proof, a type of ZK proof. A validity proof confirms that all the transactions within the batch have been computed accurately and are in agreement with the L1 blockchain's rules and consensus mechanism. This is often referred to as proving the behavior, ie that the code behaves exactly on the L2 as it would on L1.

You might be curious about the identity of the prover. Typically, the prover is a network of nodes that run ZK circuits. These circuits are tasked with generating the proof.

A couple of disclaimers about L2s:

• The granularity of proving can vary, meaning proofs might be generated per transaction or in batches.

• I'm outlining the overarching concept here.

• The prover network for each L2 solution may function differently.

The prover submits this proof to the L1. The L1, relying on the validity proof, doesn't have to check each transaction individually to confirm their integrity. It can promptly affirm and record the batch of transactions. This leads to what's known as immediate finality, where the transactions are considered finalized right away. Every L2 has a verifier smart contract deployed on L1. This smart contract verifies the validity proof. If the contract can verify the proof, the L1 can assume that the transaction are valid.

The main difference between ZK rollups and optimistic rollups lies in when the transactions are verified to be published on the L1. ZK rollups immediately include the transactions on the L1 upon submission because the L1 accepts the validity proof as assurance that the L2's ZK rollup can be trusted.

Optimistic rollups operate differently from ZK rollups; they don't offer a pre-verification proof. Instead, there's a waiting period—usually seven days—where trusted entities on the network can review the transaction. If they detect anything malicious, they have the opportunity to create and submit a fraud proof.

ZK Proofs

Circuits

Circuits are the foundational elements of ZK proofs. Essentially, ZK proofs are results from mathematical expressions that execute a computation. Inputs are used to feed data into these expressions, which then process the information according to a set of predefined rules or logic gates within the circuit, ultimately yielding an output that validates the correctness of the assertion without revealing the underlying data itself.

ZK proofs can be written as arithmetic or polynomial.

ZK Proof with Circuits Example

Situation: You wish to access the ski lift at a resort, but you want to prove you own a valid ski ticket without displaying the ticket or any personal information.

Inputs:

• A unique identifier for each ski ticket, like a digital barcode.

• A secure, cryptographic representation of the ticket holder's identity.

Circuit Functionality:

• The system verifies against a secure database that the unique identifier corresponds to a legitimate, unexpired ski ticket.

• It then confirms that the cryptographic representation matches the stored identity associated with that ski ticket.

• If both conditions are met, the system outputs a verification token indicating a valid ticket without revealing any identity details.

Proof Process:

Prover (Ski Ticket Holder):

• Generates a ZK Proof using their ticket's unique identifier and their cryptographic identity representation.

• Submits this proof to the verifier via a secure, anonymous verification system.

Verifier (Ski Lift Operator's System):

• Checks the proof without learning the ticket's details or the holder's identity.

• If the proof checks out, the lift system activates, allowing the holder to board the ski lift.

This mechanism ensures that the skier can access the ski lift with a valid ticket without ever revealing the ticket itself or any personal information, thus maintaining privacy and security.

Validity Proofs

To ensure a ZK rollup can successfully submit its batched transactions to L1, it must communicate that these transactions are legitimate. ZK rollups achieve this through the use of validity proofs, which are a form of ZK proofs.

Validity proofs are available in two flavors: zk-SNARKs and zk-STARKs.

SNARKs (Succinct Non-interactive Arguments of Knowledge): SNARKs are a type of ZK proof that is succinct (the proof size is small), non-interactive (it doesn't require active communication between the prover and verifier), and allows the prover to demonstrate knowledge of a secret without revealing it. SNARKs often rely on a setup phase that generates a common reference string (CRS) used by both the prover and the verifier. SNARKs can use both arithmetic and polynomial circuits.

STARKs (Scalable Transparent Arguments of Knowledge): STARKs are similar to SNARKs in that they provide ZK proofs without requiring interaction. However, they do not require a trusted setup (no CRS is needed) and are based on hash functions, making them post-quantum secure. STARKs utilize polynomial commitments and are transparent because they don't rely on any secret parameters.

Compatibility

EVM

The Ethereum Virtual Machine (EVM) is essentially the platform where smart contracts are executed on the Ethereum blockchain. Smart contracts are compiled into bytecode for the EVM to process, using basic instructions known as opcodes.

ZK proofs were not initially designed for compatibility with Ethereum. They originate in the field of cryptography, whereas Ethereum is part of the blockchain realm. Consequently, compatibility between ZK proofs and the EVM presents a significant challenge due to their complexities.

Zero Knowledge Ethereum Virtual Machine (zkEVM)

Ethereum, in its original form, doesn't inherently understand or validate ZK proofs. This incompatibility led to the development of the zkEVM . The zkEVM is an adapted virtual machine that's designed to interpret both the standard EVM opcodes and the specific requirements of ZK proofs.

The compatibility between the zkEVM and the standard EVM varies, and it can be considered a spectrum.

Beginning from the most compatible to the least, we will explore the current landscape, including the benefits and drawbacks of various approaches to integrating zkEVM with the standard EVM.

1. Full EVM Equivalence aims to recreate the entire Ethereum system, ensuring that everything from the high-level code to the low-level operations and the very structure of the machine is preserved.

2. Bytecode Equivalence focuses on the individual operations (opcodes) of the EVM but might allow some structural changes to the machine itself for efficiency

3. Language Equivalence aims to support Ethereum’s high-level language, Solidity or Vyper but recompiles contracts in the native VM language. The native VM language depends on the L2.

These levels of equivalence can be further broken down to highlight the specific ways they achieve compatibility with the EVM's operational framework.

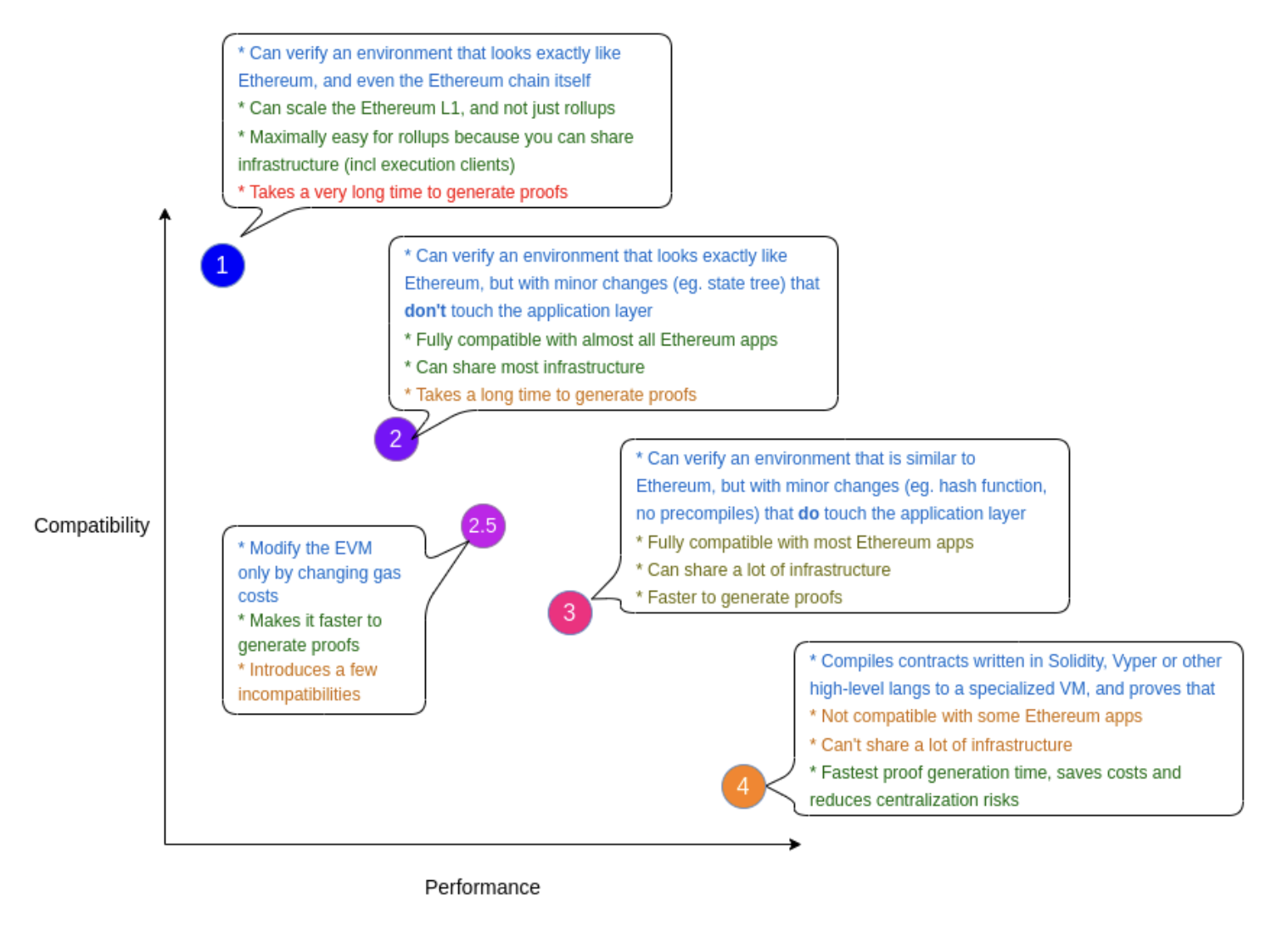
• Type 1 (fully Ethereum-equivalent)

  • Benefit:

    • Perfect compatibility with Ethereum blocks

    • Ideal for rollups due to the ability to reuse a lot of Ethereum's infrastructure

  • Drawback:

    • Very long prover times since it replicates Ethereum exactly, which wasn't designed for ZK

• Type 2 (fully EVM-equivalent)

  • Benefit:

    • Perfect equivalence at the VM level allows existing applications to work seamlessly

    • Changes to data structures improve prover times compared to Type 1

  • Drawback:

    • Still has slower prover times due to inefficiencies inherent in the EVM that remain unaddressed

• Type 2.5 (EVM-equivalent, except for gas costs)

  • Benefit:

    • Improved prover times

    • Almost fully equivalent to EVM with slightly faster approval times

  • Drawback:

    • Potential reduction in developer tooling compatibility and the need to adjust some applications due to changed gas costs

    • Some precompiles are not supported

• Type 3 (almost EVM-equivalent)

  • Benefit:

    • Easier to build and faster prover times by removing features difficult to implement.

  • Drawback:

    • More incompatibility with existing applications, which may require re-writing to adjust to the removed features

• Type 4 (high-level-language equivalent)

  • Benefit:

    • High efficiency and faster prover times by redesigning from scratch with ZK proof friendliness in mind

    • Potential for greater scaling and lower costs due to optimized design

  • Drawback

    • Lower compatibility with the existing EVM infrastructure, requiring significant changes to existing applications

    • Developer experience may be impacted due to differences from the familiar EVM environment

Conclusion

We made it. By now, you've learned basic ZK terminology, the mechanics of ZK rollups, the different types of ZK proofs and the nuances of zkEVM with its compatibility quirks.

Hopefully by now you can explain what a ZK proof to someone like they’re 5.

If there’s something I didn’t cover that you’d like me to, or perhaps you’d like me to dig a little deeper, my DMs are always open.

Until next time!

Sources