要点

• 经济模型简化了经济过程，从而降低了分析和预测通货膨胀或失业率水平等多种经济因素的难度。

• 虽然经济模型并不直接应用于加密货币市场，但它们为分析不同的加密货币指标提供了宝贵的理论知识。

• 借助经济模型，政策制定者可做出更明智的决策并制定效果更佳的政府政策，企业也可以根据预测的经济行情进行战略规划。

简介

鉴于经济规模庞大且相互关联，要想深入了解经济可能会让人无从下手。不过，经济学家们已经研究出了按照细分因素来分析整体经济的方法。在本文中，我们将探讨经济模型的概念、组成部分、类型、运作方式、在加密货币领域的用途以及部分用例。

经济模型介绍

经济模型是经济过程的简化表示，有助于经济学家和政策制定者了解经济中不同要素（例如通货膨胀和失业率）之间的相互作用。

经济模型有以下几个主要用途：

1. 它们可以解释不同经济变量之间的联系。

2. 它们可以赋能经济学家预测未来的经济趋势和事件。

3. 它们有助于评估经济政策的潜在影响。

经济模型的组成部分

变量

变量是可以改变和影响经济模型结果的因素。常见的经济变量包括：

1. 价格。购买商品或服务所需的金额。

2. 数量。生产或消费的商品或服务的数量。

3. 收入。个人或家庭的收入。

4. 利率。借款成本。

参数

参数是定义模型中变量行为的固定值。例如，在分析通货膨胀与失业率之间关系的模型中，参数可能包括自然失业率 (NRU) 和通胀对失业率变化的敏感程度。

自然失业率又称为非加速通货膨胀失业率 (NAIRU)，是劳动力市场处于均衡状态时的失业率水平。

方程

方程是描述变量与参数之间关系的数学表达式，是经济模型的支柱。

例如，菲利普斯曲线就是一个描述通货膨胀与失业率之间关系的模型。菲利普斯曲线方程可写为：

• *π = πe ​− β (u−un​)，*其中：

  • π 代表通货膨胀率。

  • πe 代表预期通货膨胀率。

  • β 是一个参数，衡量的是通货膨胀对失业率变化的敏感程度。

  • u 代表实际失业率。

  • un 代表自然失业率。

假设

假设通过针对各种因素设置某些条件或约束来简化模型。常见的假设包括：

1. 理性行为假设。消费者和企业在做决策时均以实现效用或收益最大化为目标。

2. 完全竞争假设。它假定市场上有足够多的买家和卖家，没有任何一家实体能够操纵市场。

3. 其他条件不变假设。在分析一个变量的影响时，所有其他因素保持不变。

经济模型如何运作？

1. 确定关键变量以及变量之间的关系

首先，应确定纳入模型的关键变量，并建立变量之间的关系。例如，在供给需求关系模型中，关键变量为：

• 价格 (P)。

• 需求量 (Qd)。

• 供给量 (Qs)。

这些关系就是需求曲线与供给曲线，它们展示了需求量 (Qd) 和供给量 (Qs) 如何随价格 (P) 的变化而变化。

2. 定义参数

接下来，我们收集相关数据来估算参数。在供需模型中，典型的关键参数为：

• **需求价格弹性：**衡量需求量对价格变化的敏感程度。

• **供给价格弹性：**衡量供给量对价格变化的敏感程度。

3. 建立方程

然后，建立方程来表达变量与参数之间的关系。例如，在供需模型中，方程可写为：

• Qd = aP，其中 a 代币需求价格弹性。

• Qs = bP，其中 b 代表供给价格弹性。

4. 制定假设

最后，制定假设以简化模型。这些假设界定了模型的范围和局限性，阐明了模型将考虑和不考虑的因素。例如，供需模型可基于以下假设构建：

• **完全竞争假设。**假设仅关注供需机制，忽略市场中的各种缺陷。

• **其他条件不变假设。**假设价格 (P) 变化对需求量 (Qd) 和供给量 (Qs) 的影响相互独立，以便更清晰地分析这种关系。

示例

我们以苹果市场为例，分析苹果的价格是如何由供需双方的相互作用来决定的。

1. 确定关键变量以及变量之间的关系。

该模型中的关键变量为：

• **价格 (P)。**苹果的价格。

• **需求量 (Qd)。**消费者愿意以给定价格购买的苹果数量。

• **供给量 (Qs)。**生产者愿意以给定价格出售的苹果数量。

这些关系以需求曲线与供给曲线表示，它们展示了需求量 (Qd) 和供给量 (Qs) 如何随价格的变化而变化。

2. 定义参数。

关键参数可能包括：

• **需求价格弹性。**衡量需求量对价格变化的敏感程度。

• **供给价格弹性。**衡量供给量对价格变化的敏感度。

我们假设：

• 需求价格弹性 = -50

• 供给价格弹性 = 100

上述数值代表的含义为：

• 苹果的价格每上涨 1 美元，其需求量便会减少 50 个。

• 苹果的价格每上涨 1 美元，其供给量便会增加 100 个。

3. 建立方程。

接下来，我们通过建立方程来表达上述供给量 (Qs)、需求量 (Qd) 与价格 (P) 之间的关系：

• Qd = 200 − 50P

• Qs = -50 + 100P

4.制定假设

为了简化模型，我们做出了以下假设：

• **完全竞争假设。**假设买卖双方人数众多，谁也无法控制整个市场。

• **其他条件不变假设。**假设在分析价格对需求量和供给量的影响时，所有其他因素保持不变。

5.分析市场平衡点

为求出均衡价格和均衡数量，我们设定 Qd = Qs：

200 − 50P = -50 + 100P

250 = 150P

P = 250 / 150

P = 1.67

将 P = 1.67 代入上述方程，得出：

Qd = 200 − (50*1.67)

Qd = 200 − 83.5

Qd = 116.5

Qs = −50 + (100*1.67)

Qs = −50 + 167

Qs = 117

因此，均衡价格约为 1.67 美元，均衡数量约为 117 个苹果。

6. 结果

该供需模型为我们提供了以下数据：

• 当苹果价格等于均衡价格时，消费者愿意购买的苹果数量与生产者愿意出售的苹果数量相当（即均衡数量），此时可实现市场效率最大化。

• 如果苹果价格高于 1.67 美元，供给量将超过需求量，从而导致过剩。

• 如果苹果价格低于 1.67 美元，需求量将超过供给量，从而导致短缺。

经济模型的类型

可视化模型

可视化模型使用图形和图表来表示经济概念和关系。它们有助于阐明供需曲线等概念，使之更易于解读和掌握。

实证模型

实证模型使用现实世界的数据来测试经济理论，并展示经济变量之间的关系。此类模型从数学方程入手，然后利用数据来估算变量值。例如，某个实证模型可能会显示，当利率上升 1% 时，整个国家的投资会如何变化。

数学模型

数学模型使用方程来表示经济理论和关系。此类模型可能会非常详尽，要理解此类模型，需要拥有充足的代数或微积分知识储备。例如，一个简单的数学模型便可能包含供应、需求和市场均衡方程。

预期增强模型

预期增强模型纳入了人们对未来经济变量的预期。此类模型有助于预测通货膨胀或利率等指标对经济行为的影响。例如，如果人们预计未来通胀率会提高，他们现在可能会增加消费，从而增加当前需求。

模拟模型

模拟模型利用计算机程序模拟现实世界的经济场景。借助此种模型，经济学家可使用不同的变量进行试验并查看潜在结果，无需在现实世界中测试这些场景。这有助于分析政策或经济冲击的潜在影响。

静态和动态模型

静态模型提供特定时点的经济概况。由于此类模型未考虑随时间推移而发生的变化，因此更易于使用。例如，供需模型仅显示市场均衡点，未考虑市场会如何根据变化进行调整。

相比之下，动态模型将时间纳入考量，显示经济变量如何随时间推移而发生变化。此类模型展示了经济状况如何随政策变化或外部冲击等多种因素的变化而变化。动态模型通常更为复杂，但有助于人们更好地了解长期经济趋势和经济周期。

加密货币领域的经济模型

了解市场行情

经济模型有助于我们了解供需情况如何影响加密货币价格。通过分析可用代币数量（供给量）和有意购买代币的人数（需求量），我们可以大致了解代币价格走势和市场趋势。

分析交易成本

交易成本模型向我们展示了手续费对区块链网络的影响。如果交易手续费高昂，网络普及可能会受到阻碍，相反，如果手续费低廉，可能会推动其普及。通过分析交易成本，我们可以预测其对用户行为和网络效率的影响。

模拟经济场景

借助模拟模型，我们可以创建虚拟场景，观察不同变量对加密货币市场的影响。这些模型可用于模拟监管变化、技术进步或用户行为转变。模拟模型虽然是理论性的，但它们为分析未来的潜在发展提供了框架。

局限

假设不切实际

许多经济模型所依赖的假设在现实中并不总是成立。例如，模型可能会使用完全竞争假设或理性行为假设，但在实际市场中，这些假设并不总是成立。因此，这些假设会限制模型在实际应用中的适用性和准确性。

过于简化

经济模型对复杂的实际情况进行了简化，使其更易于分析。这意味着，它们可能会忽略一些重要因素，从而导致结果可能无法完全体现真实的经济状况。例如，模型可能会假设所有消费者的行为方式相同，而忽略了可能影响经济结果的个体差异。

用例

政策分析

经济模型可用于评估不同政府政策的潜在影响。例如，它们可以展示减税、政府支出增加或利率变动所带来的影响。这有助于政策制定者做出更明智的决策，制定出更有效的政策。

预测

经济模型可用于预测未来的经济趋势，有助于企业和政府做好未来规划。例如，模型可以预测未来几年的经济增长率、失业率或通货膨胀率。

企业规划

企业可利用经济模型，根据预测的经济行情进行战略规划。例如，企业可利用模型来预测其产品的需求量，并据此规划产量。

经济模型示例

供需模型

供需模型展示了市场中商品的价格和数量是如何确定的。它使用供给曲线（显示生产者在不同价格下的销售量）和需求曲线（显示消费者在不同价格下的购买量）两条曲线。两条曲线的交点即为市场均衡点，从而确定了销售价格和数量。

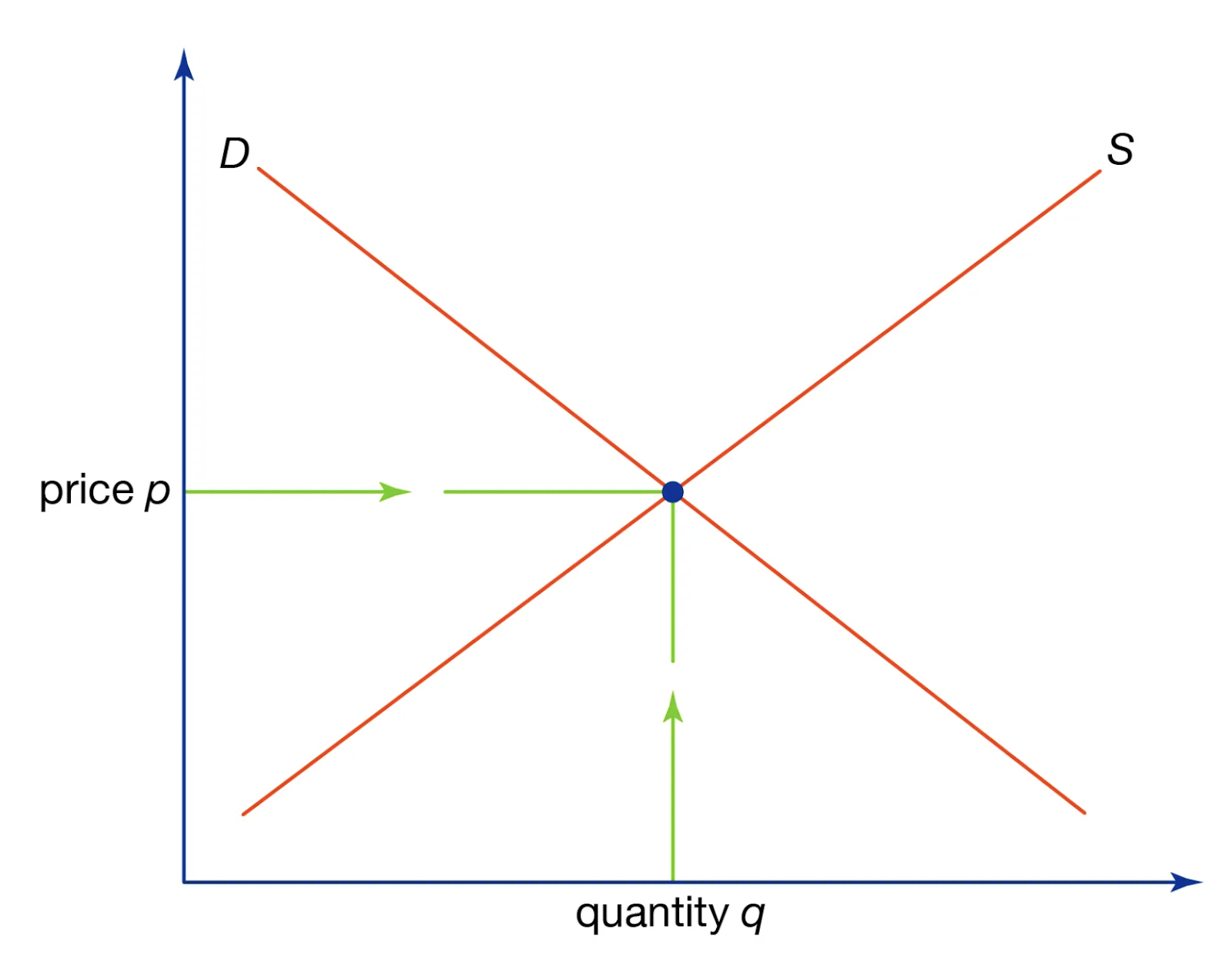
IS-LM 模型

IS-LM 模型阐释了商品市场和货币市场中利率与实际产出之间的关系。IS 曲线代表商品市场达到均衡状态，而 LM 曲线则代表货币市场达到均衡状态。两条曲线的交点即为一般均衡，此时两个市场均达到均衡状态。

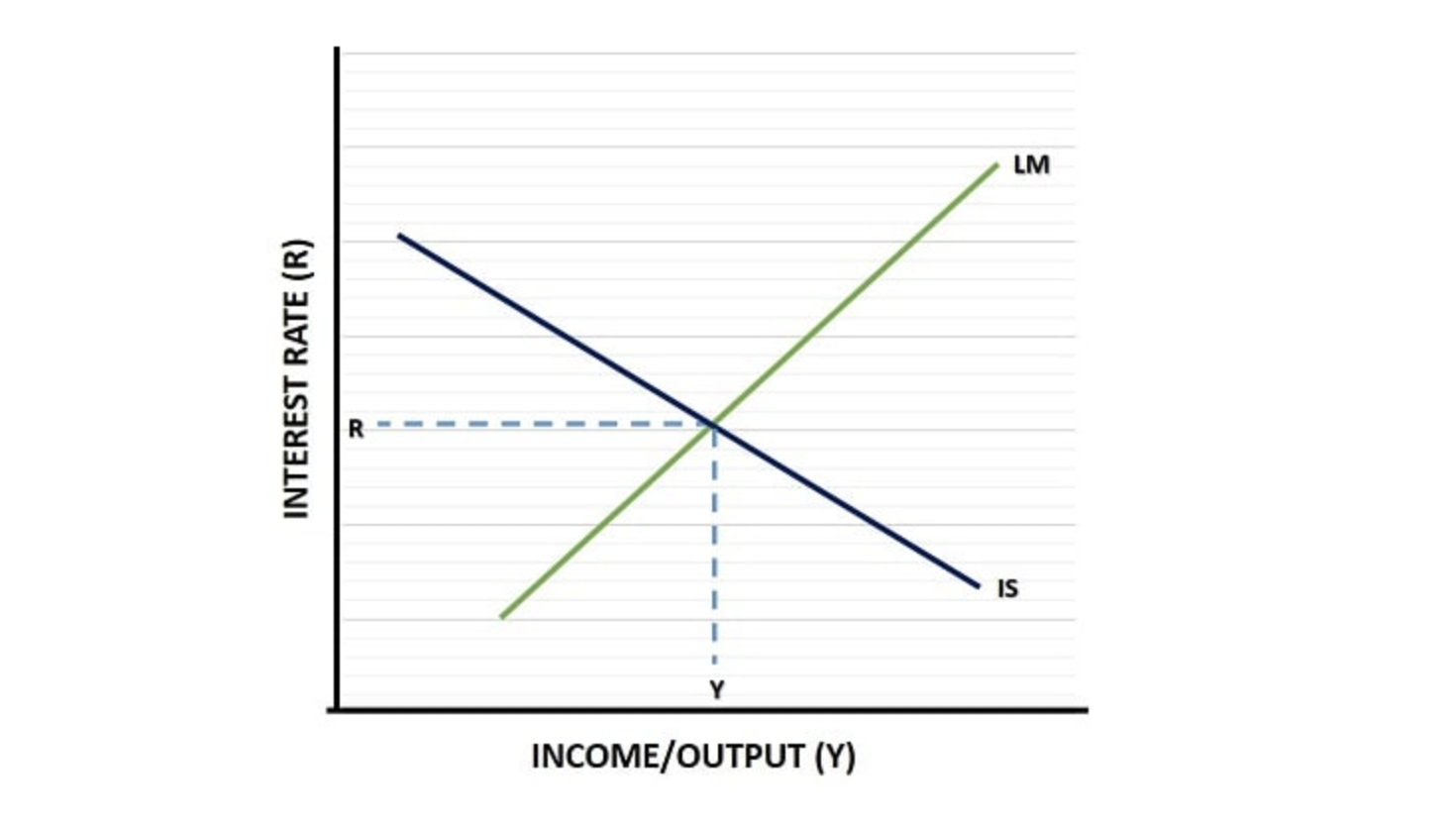
菲利普斯曲线

菲利普斯曲线阐明了通货膨胀与失业率之间的关系。它表明，当通胀率上升时，失业率往往会下降，反之亦然。该模型有助于政策制定者了解如何在管理通胀和失业率之间权衡取舍。

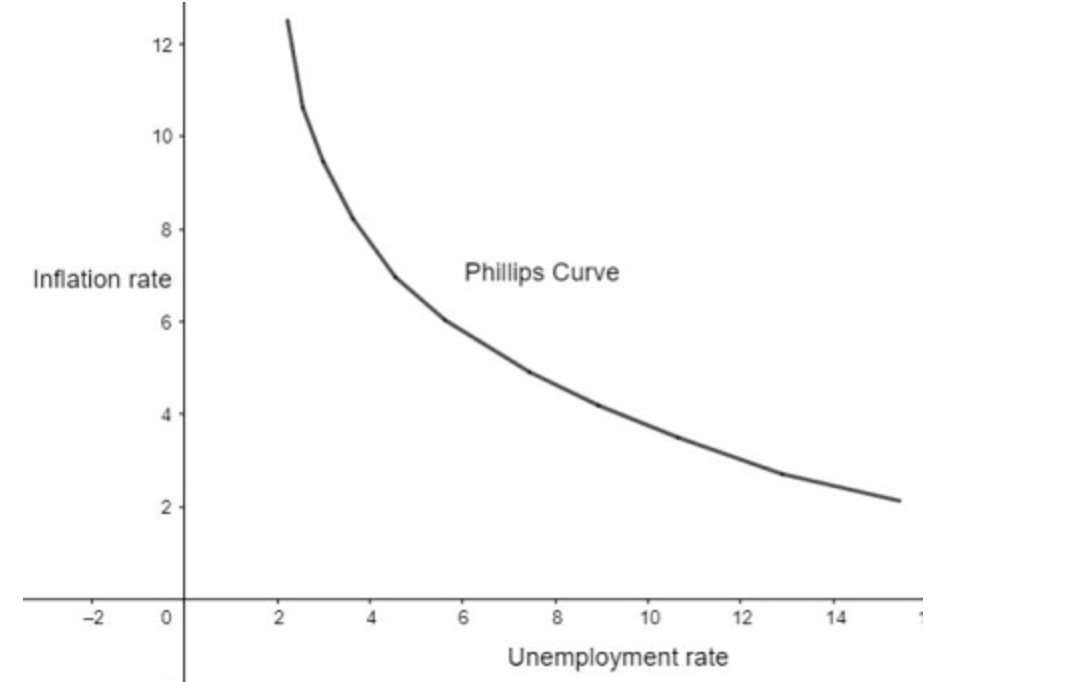
索洛增长模型

索洛增长模型聚焦劳动力、资本积累和技术进步，以此来研究长期经济增长。它展示了这些因素如何促进稳态增长，即经济以恒定速度增长。

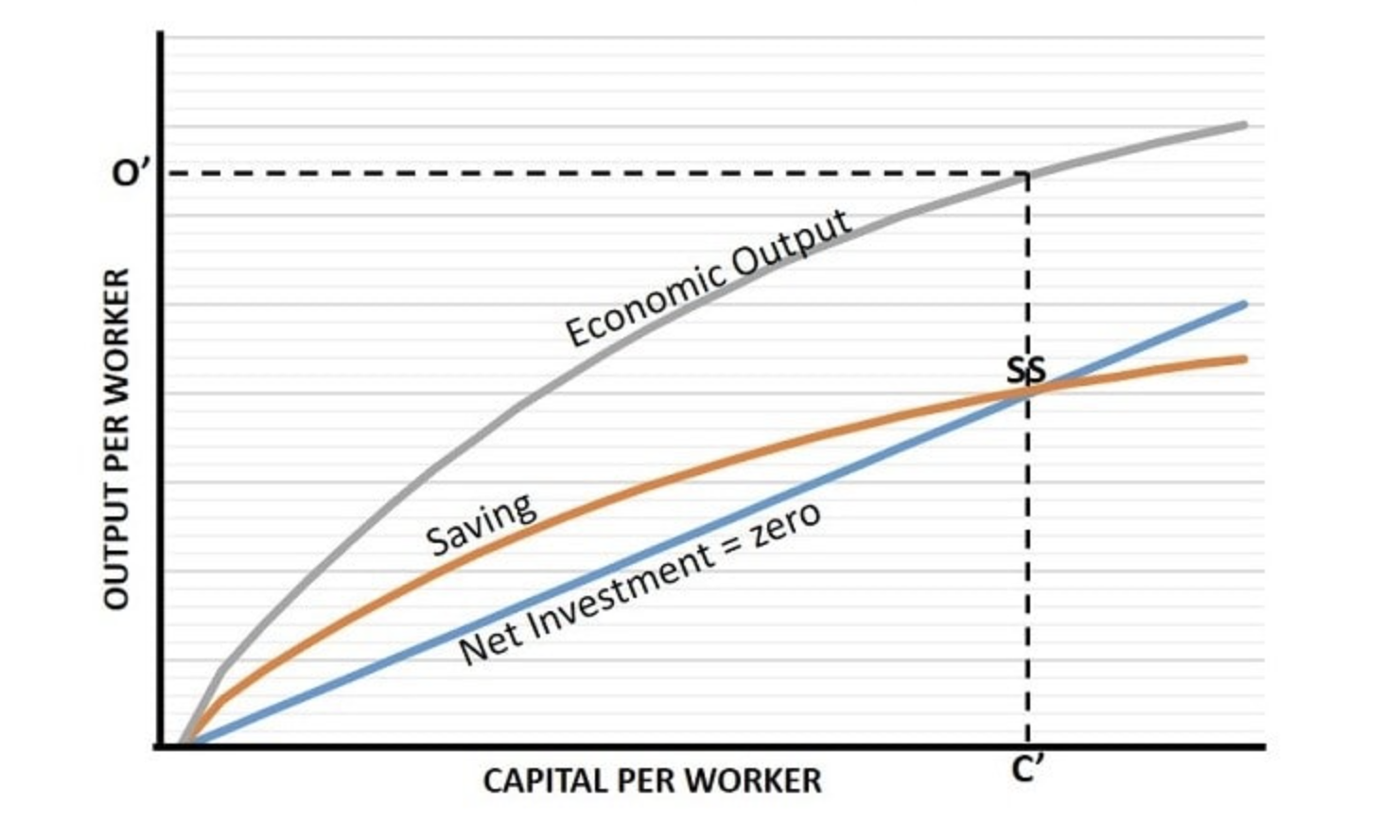
结语

经济模型简化并阐明了经济的运作机制。它们将复杂的经济相互作用拆解为易于理解的因素，从而解释不同因素如何影响经济结果。经济模型有助于政策制定者做出明智的决策，还可助力企业进行战略规划。就加密货币领域而言，模型可以提供理论知识，用于分析市场行情和交易成本以及模拟未来可能会出现的场景，助力人们了解不同因素会如何影响加密货币市场。