前两天《暗黑森林中的共赢之道:加密货币市场的进化博弈》发出后,很多人对文章中提到的进化博弈理论很感兴趣,所以特地找了斯坦福哲学百科中关于进化博弈理论的文章(https://plato.stanford.edu/entries/game-evolutionary)。 此文高度概括了这套理论,同时给出了扩展阅读的索引。

有意思的是在文章中的“应用”一章中,详细论述了通过进化博弈过程达到资源公平分配的可行性。考虑到参与博弈的玩家都是理性自私的,所以这个推论让我们看到了在一个由理性的、自私的、自由的个体组成的群体中,实现公平分配的可能性,以及决定分配公平的关键因素:参与者相关性。
以下是翻译的内容
研究公平感进化的一个博弈案例是“分蛋糕”(这是纳什谈判博弈的最简单版本)。在《社会契约的演化》的第一章中,Skyrms如下阐述了这个问题:
我们从一个非常简单的问题开始;我们要在我们之间分一块巧克力蛋糕。我们之间没有特殊的索取权。我们的立场完全对称。蛋糕对我们来说是一笔意外之财,我们需要决定如何分割。如果我们无法达成一致,蛋糕就会变坏,我们将一无所获。(Skyrms,1996年,第3-4页)
把上述问题用数学语言转化为通用问题,就是:假设两个个体由第三方提供一份大小为C的资源。在这个博弈中,玩家的策略是他想要的蛋糕数量。玩家的策略集合是0到C之间的任何数量。如果每个玩家的策略之和小于或等于C,那么每个玩家都会得到他所要求的数量。然而,如果策略之和超过 C,那么没有玩家会得到任何东西。图13说明了这个博弈的可行策略集合。

我们可以清晰地感觉到每个玩家选择的“显而易见”策略是C/2;其哲学问题在于解释为什么玩家会选择这个策略而不是其他策略。即使在完全对称的情况下,回答这个问题比起初看起来更加困难。
为回答这个问题,我们首先注意到这个博弈有无穷多个纳什均衡。如果玩家1要求蛋糕的一部分p,其中0≤p≤C,而玩家2要求C−p的部分,那么对于p∈[0,C]的任何值,这个策略配置都是一个纳什均衡。(每个玩家的策略都是对方选择的最佳反应,即没有一方可以通过改变自己的策略来提高自己的收益。)因此,平均分配只是无穷多个纳什均衡中的一个。
有人可能会提出,如果玩家们认为他们不确定自己将被分配为玩家1还是玩家2,他们应该选择能够最大化期望收益的策略。Skyrms指出,这个建议本质上就是Harsanyi(1953年)的观点。然而,这个观点存在问题,即如果玩家只关心他们的期望收益,并且认为自己被分配为玩家1或玩家2的可能性是相等的,那么这个观点也无法唯一选择平均分配。考虑策略配置⟨p,C−p⟩,将p份分给玩家1,将C−p份分给玩家2。如果一个玩家认为自己被分配为玩家1或玩家2的可能性相等,那么他的期望效用就是
\frac 12 p + \frac 12(C−p)=\frac C2
且p∈[0,C]
现在考虑以下进化模型:假设我们有一个群体,他们成组地进行分蛋糕游戏,并在一段时间内根据动态复制策略(*见文末注释)来修改他们的策略。为了方便起见,让我们假设蛋糕被均匀地划分为10份,并且每个玩家的策略符合以下11种可能的类型之一:要求0份、要求1份、...、要求10份。对于动态复制策略,群体的状态由向量⟨p0,p1,…,p10⟩表示,其中每个pi表示群体中“要求i份”的策略的频率。
动态复制策略使我们能够模拟随着时间的推移,群体中策略的分布如何从特定的初始条件开始随时间变化。下图14显示了在连续动态复制策略下的两种进化结果。请注意,尽管公平分配可以演化出来,如图14(a)所示,但它并不是唯一的进化稳定结果,正如图14(b)所示。
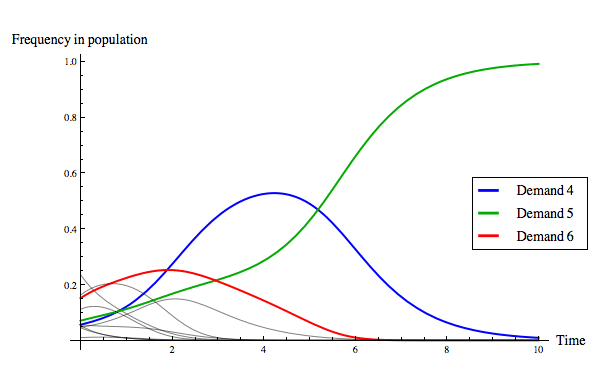
图14:分蛋糕博弈在连续动态复制策略下的两种进化结果。在11种策略中,只有三种被着色以在图中可辨认,如图例所示。
回想一下,我们的任务是解释: 为什么我们认为在一个完全对称的资源分配问题中,“显而易见”的策略选择是两个玩家都要求资源的一半。 (虽然这个结果貌似人人都能想到,但仍需要从数学上进行证明) 上面的内容表明,在一个有限理性的群体中,他们以动态复制策略描述的方式修改自己的行为,公平分配是一个进化结果,尽管不是唯一的结果。公平分配的趋势出现时,假设任何初始条件都是等可能的,可以通过确定整个群体中使用“要求5份”的策略的状态的吸引域的大小来衡量。Skyrms(1996年)使用蒙特卡洛方法来测量公平分配的吸引域的大小,发现公平分配大约出现了62%的概率。
然而,重要的是要意识到动态复制策略假设个体之间的任何两两相互作用是等可能的。事实上,个体之间的相互作用往往在某种程度上是不确定的。相互作用的强度可以由空间位置(如上面所示的空间囚徒困境的情况)、社会关系的结构效应、获取信息的完整度、内外群体成员资格的影响等多种原因引起。
当引入相关性强度时,公平分配出现的频率也会发生戏剧性的变化。模型中的相关性强度由相关系数 ε 表示,它的取值范围在 0 到 1 之间。
-
当 ε = 0 时,完全没有相关性,双方交互的可能性仅由群体中遵循特定策略的个体比例决定。
-
当 ε = 1 时,相关性是完美的,遵循特定策略的个体只与同类进行交互。
中等程度的相关性会导致个体倾向于与同类进行交互,这种倾向随 ε 的增加而增加。图15展示了当相关系数 ε 从0增加到0.2时,全体要求5份的吸引域的变化情况。一旦交互中的相关性达到 ε = 0.2,公平分配几乎成为一种进化的必然。
请注意,这并不依赖于只存在三种策略:允许一定的交互相关性增加了公平分配演化的概率,即使初始条件包含使用任意一种可能策略的个体。

图15:三个图表展示了随着交互中的相关性强度增加,公平分配进化的可能性会更高。在图15(a)和15(b)中,空间内部存在一个不稳定的固定点,该点上群体中存在所有三种策略。(这是进化轨迹似乎相交的点。)根据动力系统理论,这个固定点被称为鞍点(saddle point):最小的扰动将使群体从该点演化到其他两个吸引点之一。
从这个模型中我们可以得出什么关于公平分配演化的结论呢?当然,这取决于动态复制策略对作用于人类群体的主要进化力量(文化或生物)的准确建模程度。虽然动态复制策略是一个“简单”的数学模型,但它足以模拟生物进化的一种类型(参见Taylor和Jonker,1978)和文化进化的一种类型(参见Börgers和Sarin,1996;Weibull,1995)。正如Skyrms(1996)所指出的:
在有限的人口中,在有限的时间内,在进化中存在一些随机因素,在物品的可划分性和一定程度的相关性存在的情况下,我们可以说,在分蛋糕的情况下,很有可能会演化出类似“分享与平均分享”的行为。这或许是对我们关于正义概念起源的一个开始的解释。
当然,这种观点并不是没有争议的。有关讨论的一些选集请参见D'Arms(1996, 2000);D'Arms等人(1998);Danielson(1998);Bicchieri(1999);Kitcher(1999);Gintis(2000);Harms(2000);Krebs(2000);Alexander和Skyrms(1999);以及Alexander(2000, 2007)。
动态复制策略(The Replicator Dynamics): 假设每个玩家随机选择人群中的另一个人(所有个体被选择的可能性相等),并将他们在上一轮游戏中的收益与被选择人的收益进行比较。如果被选择的人获得了更高的收益,那么玩家以与收益差异成比例的概率采用被选择人使用的策略。Schlag(1998年)证明了这个学习规则产生了复制动力学。
点评
在翻译上面这段文字的时候,我想到了平等和自由两个政治学概念。这是一切政治和社会问题或矛盾的出发点。
公平到底应该通过平等去实现,还是通过自由去实现?
古今中外几千年来,无数哲人讨论过这个问题,但至今尚无定论。对于这个问题的不同解答,形成了当今世界上两大立场对立的群体。
进化博弈论从数学、博弈论和生物学角度阐述了这么一个事实:理性的自私是公平的出发点,自由是公平的保障。 当参与者无法自由的产生互动,是无法达成公平的纳什均衡。同样的结论,哈耶克在《通往奴役之路》一书中也表达了类似的观点,即:追求實現人人平等分配這個崇高理想過程,就是一條通往奴役之路。