首要特点：棋盘中的每个点即都是中心，又都不是中心。

1．缘起

  棋类游戏一般由以下要素构成：①规则②棋子③先后④棋盘。如何使棋类游戏做到公平那？对于①来讲，显然暗棋（例如军旗）有很多运气成分，无法做到公平。对于②来讲，无论是中国象棋，还是国际象棋，每种棋子都有各自行棋规则，显然也无法公平。对于③来讲，所有棋类游戏的对阵双方或多方无法做到同时行棋，必然存在先手的问题，围棋对于先手贴目，相对而言是最公平的，其它棋类都无法做到。

  综上所述，显然围棋做到了①②③的公平，对于④来讲，围棋显然无法做到公平，从术语“金角银边草肚皮”就可以明显看出。那如何在围棋的基础上构建一个公平的棋盘那？

2．棋盘的构思

  围棋棋盘是由19X19的经纬线构成的，中间交叉点的周围有相邻4个点，边上交叉点的周围有相邻3个点，角上交叉点的周围有相邻2个点。造成这种现象的原因是其在一个有边界的平面上构成。

  因此，必须得在一个无边界（例如球面）的面上构建围棋棋盘。如果直接在球面上构建，传统的经纬线会形成极点，也无法满足要求。以下采用两种方法构建，首先对围棋外围边上的点沿顺时针进行编号，如下图所示。

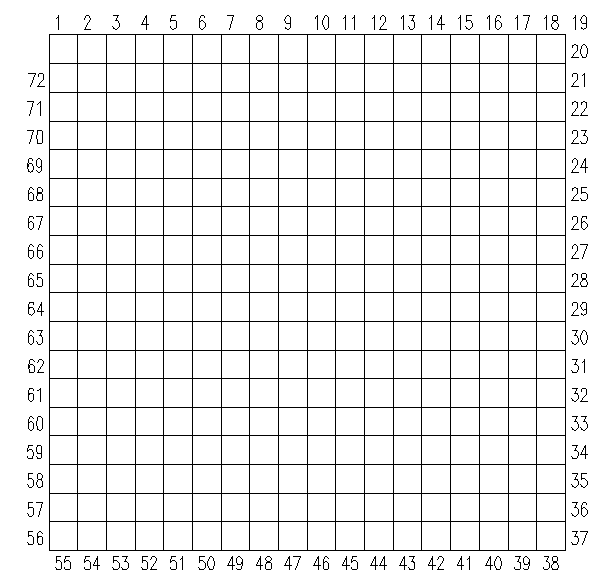
2.1 双圆柱式

  对于围棋的经线和纬线全部卷起来形成圆柱状，然后再分别展开如下图所示。

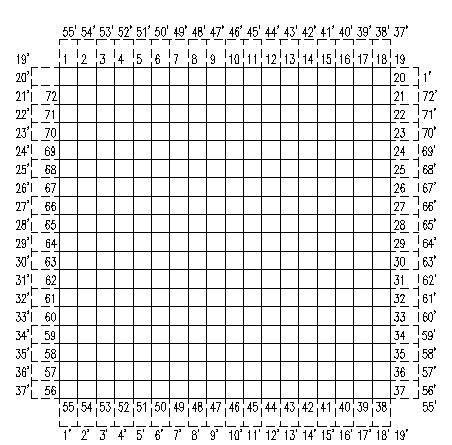
    其中点m和点m’是同一个点，例如原来的角部点1（与那里只有2和72两个相邻点）会有4个相邻点2,72,55’（就是55）和19’（就是19）。

2.2 单圆柱+莫比乌斯面式

   对于围棋的经线（或纬线）形成圆柱状，对于纬线（或经线）形成莫比乌斯面，然后再分别展开如下图所示。

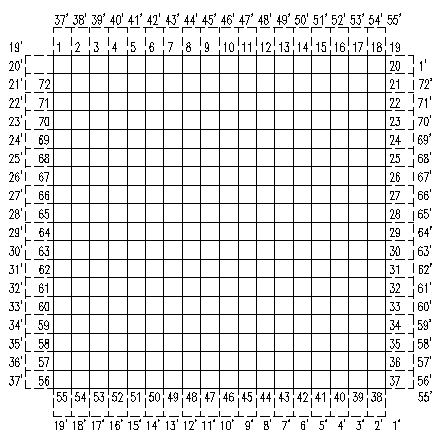
  事实上，无法同时对经线和纬线进行莫比乌斯面变换然后展开，因为此时角部的点仅仅有3个相邻点。

  以上两种构思显然做到了④棋盘公平。

3．行棋规则

   1，不准在纯虚线交点处下棋（即m’点处）。

  2，如果在m点处行棋，则同时在m’点处虚摆一子，以作标记。

  3，计算输赢时，虚线交点处（即m’点处）不计算在内。

  4，其余规则同现行围棋。

4．问题与猜想

  1，无边界围棋的先手贴目数是否与现行围棋相同，作者认为应该小于现行贴目数，原因是没有了边角优势。

  2，以上两种棋盘构思对于先手贴目来讲是否相同，作者认为仅就贴目来说两者是等价的，因此可仅采用一种即可。

5．编后语

  其实对于无边界围棋来讲，就是所有交叉点都是等价的，即都是中心，又都不是中心。借用现在流行术语也可以叫做去中心化围棋。