zkPoS: End-to-End Trustless

ORA

0x85d6

Draft

Checkout our latest Litepaper here:

https://mirror.xyz/hyperoracleblog.eth/FKvpIGI7fiuNr5rnTlFWAdxk4QCNFIR9rmqDPxWLc2w

Written by @msfew, @Shuyang

Thanks to Jules de Smit, Sinka, and Guo Yu for review and feedback.

Intro

Our previous blog talks about zkWASM and the reason why zkWASM is the perfect basis with general computation, to support flexibility for any user-defined zkGraph of Hyper Oracle’s indexing and automation protocol.

This blog covers zkPoS and how zkPoS is the most important piece of puzzle, with the ability of proving the consensus with ZK, to complete end-to-end trustlessness of Hyper Oracle’s indexing and automation protocol.

TLDR

Hyper Oracle is working on zkPoS (prove Ethereum PoS consensus with zero knowledge proof). zkPoS will enable Hyper Oracle’s zkMiddleware to be end-to-end trustless.
For achieving zkPoS Attestation, we researched all the key modules and logic (proposer selection algorithm, committee shuffling logic…) of Ethereum’s PoS consensus and listed the SNARKified design of them.
For verifying BLS signatures in zkPoS, we implemented (probably the first) open-source Halo2 Pairing library.
For further boosting zkPoS Attestation’s succinctness, we proposed the design of recursive proof for consensus of sequential blocks.

0. Ethereum PoS Consensus

Ethereum is now based on the PoS protocol of Gasper.

PoS is the Sybil resistance mechanism (restrict who can participate in the block production process) Ethereum 2.0 has.

Gasper is the actual PoS consensus protocol with the combination of FFG Casper (finality gadget) and (a variation of) LMD-GHOST (fork choice rule).

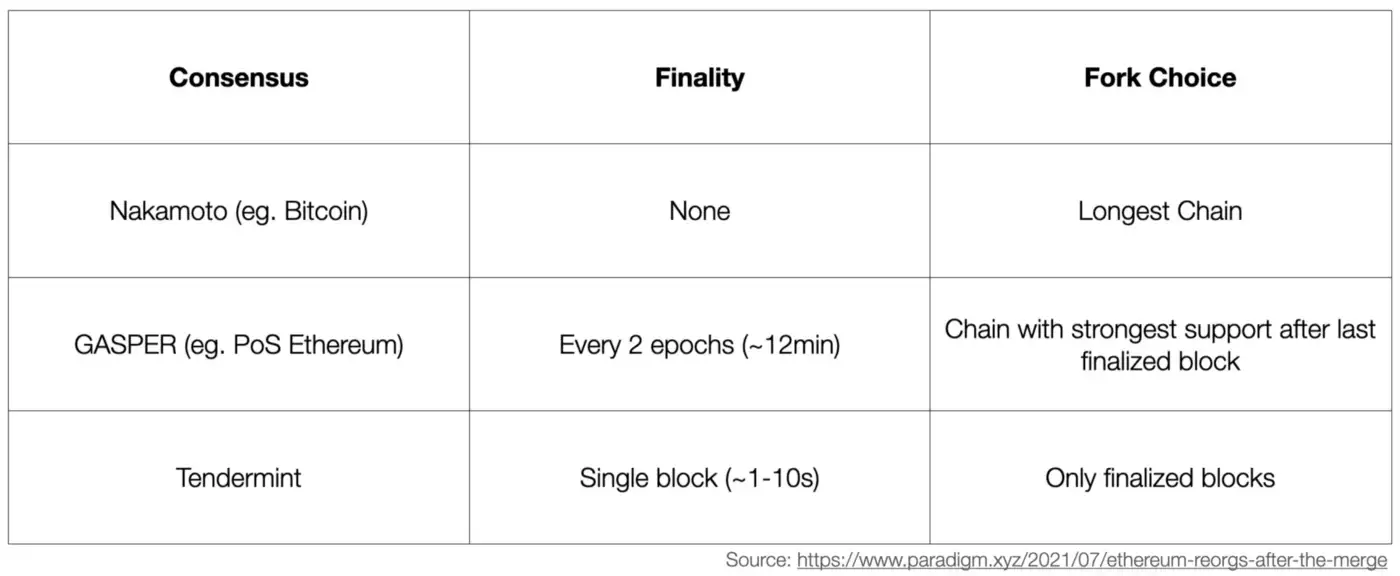
Just like the term of zk rollup is more widely used than the one of validity rollup, in this post, we will refer to Ethereum 2.0’s consensus as Ethereum PoS.

You can explore the related roadmap of Ethereum PoS consensus future by Vitalik: Paths toward single-slot finality.

a) Ethereum PoS: Terms

Now that we can dive into the actual concepts of Ethereum PoS.

Block: A block (or a slot) is generated every 12 seconds.
Epoch: An epoch is composed of every 32 consecutive blocks, with the first block as a checkpoint.
Validator and Committee: The set of validators is partitioned into committees that shuffled every epoch.
Validator Entrance: To become a validator, a node need to deposit at least 32 ETH and enter the entrance queue for no less than four epochs.
Validator Exit: To exit the validator set and reclaim balance, the validator has to stay in an exit queue for no less than four epochs. After exiting the set, there is still a ~27-hour period before being able to withdraw.

b) Ethereum PoS: Committee Attestation

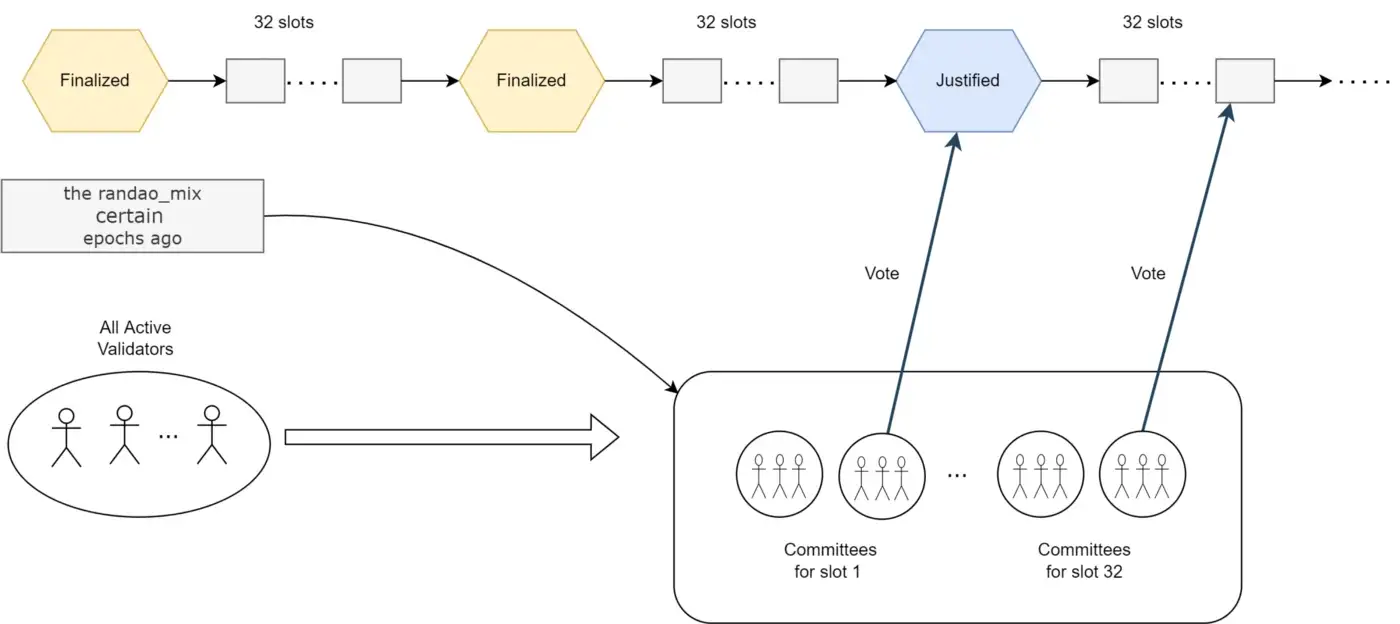
Each validator in a given committee is mapped into a set of blocks to verify each epoch. The committee is assigned by randao_mix to attest the block.

The attestation from a committee to a block contains a bit-string representing the votes and an aggregated signature (We will discuss this in later sections).

A checkpoint is justified after the blocks between it and the previous checkpoint contain at least 2/3 of the total votes. A justified checkpoint will be considered finalized after its successive checkpoint is also justified. Other blocks are justified or finalized when the nearest subsequent checkpoint is justified or finalized.

c) ZK Attestation and Committee Attestation

Attestation in zkPoS Attestation ≠ Attestation in Committee Attestation

To avoid confusion, we need to emphasize that the “attestation” in this section is essentially a local representation of votes for a particular block, which differs from the zkPoS Attestation of a global state we have realized (ZK Attestation).

1. zkPoS Attestation

a) Verify Consensus

Before understanding zkPoS, we need to know some basics of different definitions of blockchain nodes.

In Ethereum PoS’s context, an easier framing of blockchain nodes is:

Validator: build, propose, and agree on valid blocks
Full Node: download the entire block, including headers and transactions; can self-verify blocks and applies state changes
Light Client (or Light Node): download only block headers; can verify Merkle proof to check for transaction inclusion; need to “trust” other nodes on consensus for transaction data
Other types include Proposer and Builder in PBS and Archive Node

We will then only focus on Light Clients because it’s impossible for ordinary users to run Full Nodes. Apart from “ordinary users,” these scenarios are only limited to Light Client-like nodes: Mobile, Browser, and On-chain.

Light Client also has different types. They can be classified as verifiers for various usages:

Consensus Verifier: verify Merkle proof, making sure part of the consensus (transaction inclusion) is valid, but still need to trust other nodes on the whole consensus
State Verifier: verify zk or fraud proof, making sure state transition is valid
DA Verifier: verify the availability of transaction data for a newly proposed block
Full Verifier: verify all the above of consensus, state, and DA

It needs to be noted that Consensus Verifier Light Client still needs to trust other nodes on the whole consensus. Since it can verify proofs, why not let it verify ZKP of the entire consensus of Ethereum PoS?

b) Don’t Trust, Verify zkPoS Attestation

In Hyper Oracle’s vision, we are aiming at end-to-end trustlessness.

We need to implement Light Client that verifies the whole consensus of Ethereum PoS. In Ethereum’s Roadmap’s The Verge, it is also called “SNARK-based Light Client”.

The advantages of zkPoS Attestation are:

Trustless: remove Ethereum Light Client’s additional trust on other nodes to achieve full trustlessness
Decentralized: Ethereum nodes don’t need to rely on centralized services to feed them block headers or other data
Low Overhead: verification of zkPoS Attestation is efficient and requires minimal overhead

This super-powered Light Client will verify ZKP of our zkPoS Attestation (or zkPoS Proof). It can be simply run in web apps or plugins in the browser.

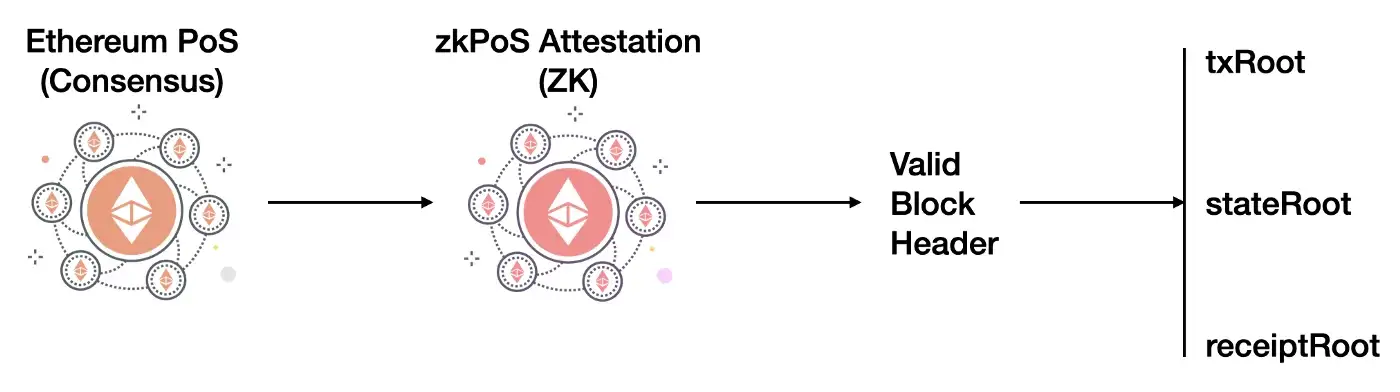
Verifying zkPoS Attestation will be the prerequisite for making everything of Hyper Oracle ZK-powered. It will give our meta apps of zkIndexing (Trustless Indexing and Querying with GraphQL) and zkAutomation (Trustless Automation and Keeper with GraphQL off-chain source) the ability to access and sync valid block headers.

After that, we can grab the receipt, state, and transaction roots with the valid block headers. In zkIndexing’s case, we follow the pipeline of receipt root, then receipts encoded data, and finally get contract events based on receipts raw data with Recursive-length prefix (RLP) decoding.

2. Hyper Oracle’s zkPoS

The algorithms of PoS are very complex, and difficult to be described in a simple diagram or a single paragraph. Also, implementing them in a ZK way requires a lot of engineering work and architectural considerations (just like zkEVM). Therefore, to implement zkPoS, it is necessary to split up the components and conquer them one by one.

The most prioritized algorithm of zkPoS is the Block Attestation. In another term, verifying BLS signatures with Pairing is the most crucial part of zkPoS. We will cover this part in detail in the later sections.

In a nutshell, for Hyper Oracle’s zkPoS, we will implement these algorithms of Ethereum PoS:

a) Randomness-based Algorithm

Proposer Selection Algorithm

A random seed before a few epochs will determine the proposer of each block.

One of this algorithm’s underlying components is the shuffling algorithm, which will also be applied in the next logic.

Committee Shuffling Logic

Every epoch, with the random seed and the shuffling algorithm, the whole set of validators is reshuffled into different committees.

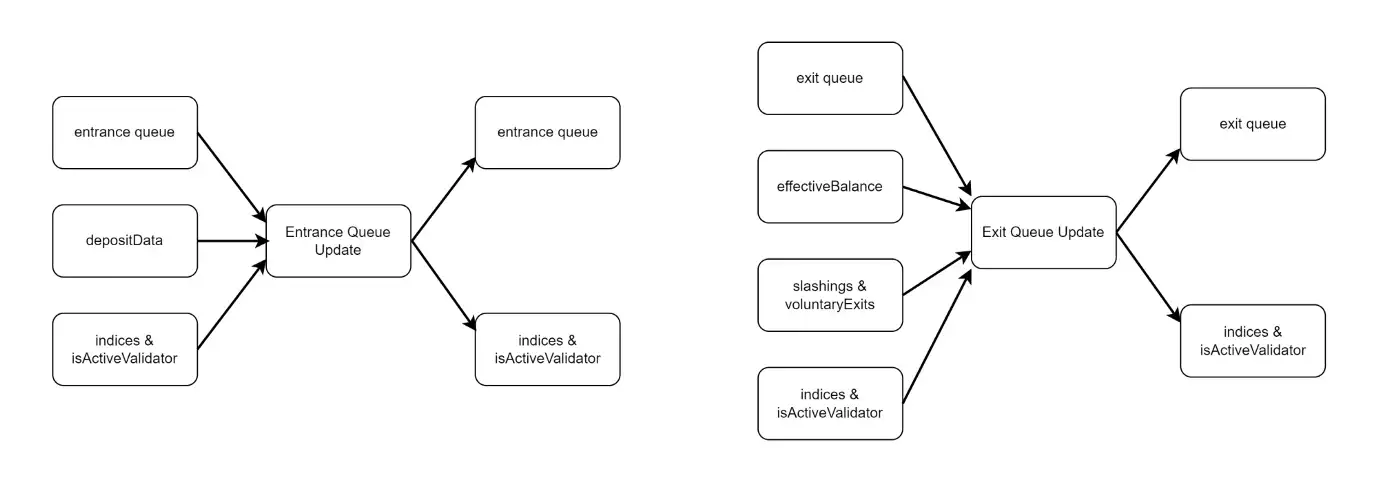
Validator Entrance

Validator candidate: Any node deposits ≥32ETH to become a validator candidate.

Formal validator: After a validator candidate enters a queue for no less than 4 epochs, it will be activated as a formal validator.

Validator Exiting

To leave the validator set and withdraw the balance, a node has to enter exit queue for no less than 4 epochs. Such validator exiting can be triggered by voluntary exits or slashing for misbehaviors.

In particular, validators with an effective balance lower than 16ETH will be inactivated.

c) Block Attestation Algorithm

A block is attested only if the corresponding committee members of the epoch have a majority (i.e., 2/3) of votes in favor of the block.

This is realized in the form of aggregated signatures and bit-strings standing for the votes where each bit is 1 if and only if the corresponding validator votes.

d) Other Logics

Note that the variables and reasonings illustrated in this article are the most significant components, but more is needed for fully attesting a block. For example, the randomness and the effective balance are not generated trivially.

Randomness

Randomness is referring to the process that a signature (randao_reveal) is mixed into a random source (randao_mix) in every block to determine the random numbers after certain blocks.

Effective Balance

The effective balance of a validator needs to be constantly updated and validators with insufficient balance will be deactivated.

e) zkPoS in One Graph

Due to the complexity of specifying the existing PoS of Ethereum, we provide this figure summarizing the above logic. The two columns represent the data corresponding to two adjacent blocks.

In particular, the first block (on the left) is a checkpoint. The figure includes the necessary (not sufficient) algorithms for the state transition from the checkpoint block to its next block.

Each arrow corresponds to at least one constraint to zkPoS Attestation.

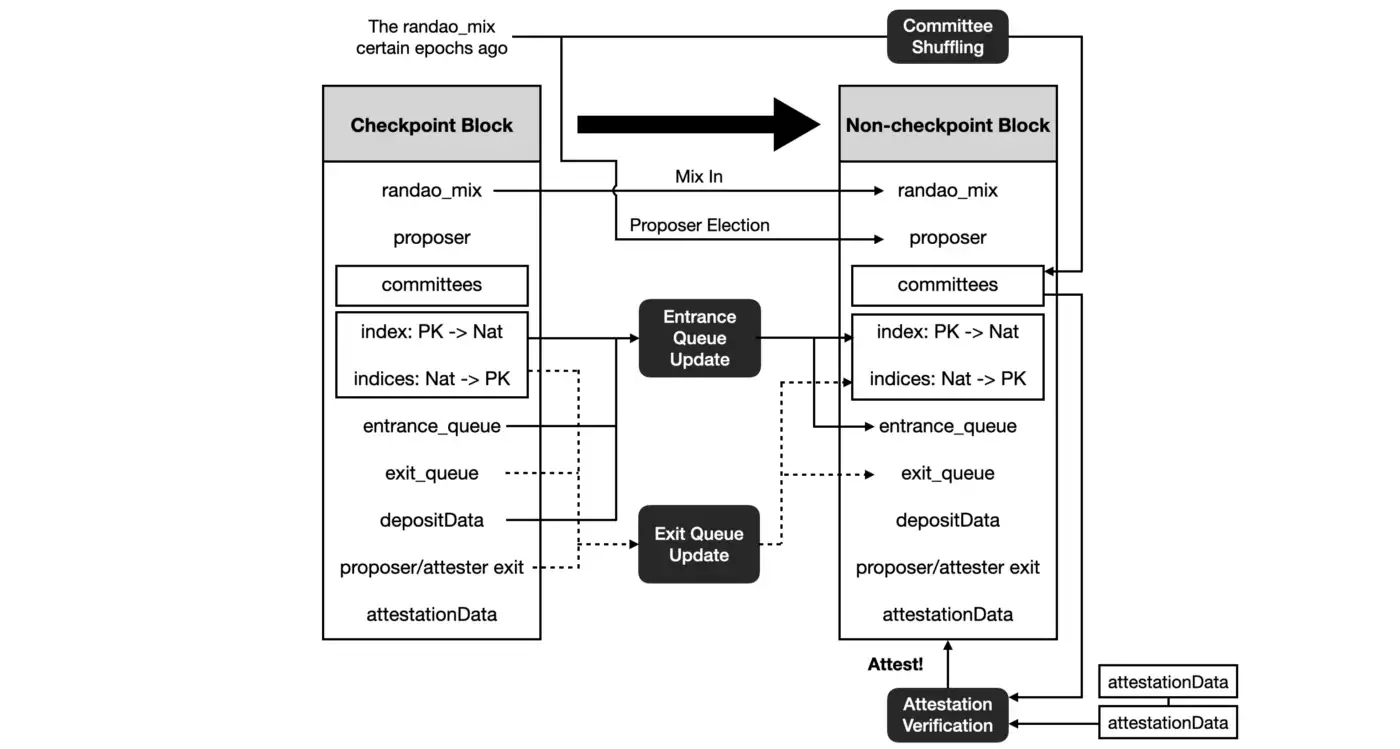
In this figure, we have omitted both effective balance and the Boolean array indicating whether an index is active for simplicity.

Notice that:

The committee members are selected according to a random number of certain epochs ago.
The entrance and exit queues are updated according to the newest deposits, slashing, and voluntary exits.
Validators in entrance/exit queue joined 4 epochs ago will leave the queue and become activated/deactivated.
The second block is attested by attestations from the corresponding committees which are stored in later blocks.

3. zkPoS: BLS

a) BLS Signatures in PoS

In Ethereum PoS protocol, BLS signatures with BLS12–381 elliptic curve are used, instead of ECDSA with secp256k1 elliptic curve (for user transaction signing).

Here are some thought processes why BLS with BLS12–381 is chosen:

1. Why BLS? BLS has the special property of pairing.

2. Why pairing? Pairing allows signatures to be aggregated.

3. Why Aggregation? Although verification of BLS signature is resource intensive and expensive compared to ECDSA due to pairing operations, the benefits are:

Time: verify all attestations in a single signature verification operation (verify N signatures with just two pairing and trivial elliptic curve point additions).
Space: scale down N bytes of all signatures to 1/N bytes of aggregate signature (approximately and ideally).
The benefits accrue when the number of signatures is more significant.

4. Why BLS12–381? **BLS12–381 is a pairing-friendly elliptic curve, with **128 bit security.

b) Verifying BLS Signature

For verifying BLS signature, we need three inputs:

BLS signature itself (”Add” signatures together with elliptic curve point addition, and get the final point representing the 96-byte signature.)
Aggregated public key (Original public keys of the validators can be found in the beacon state. Then “add” them together.)
Message

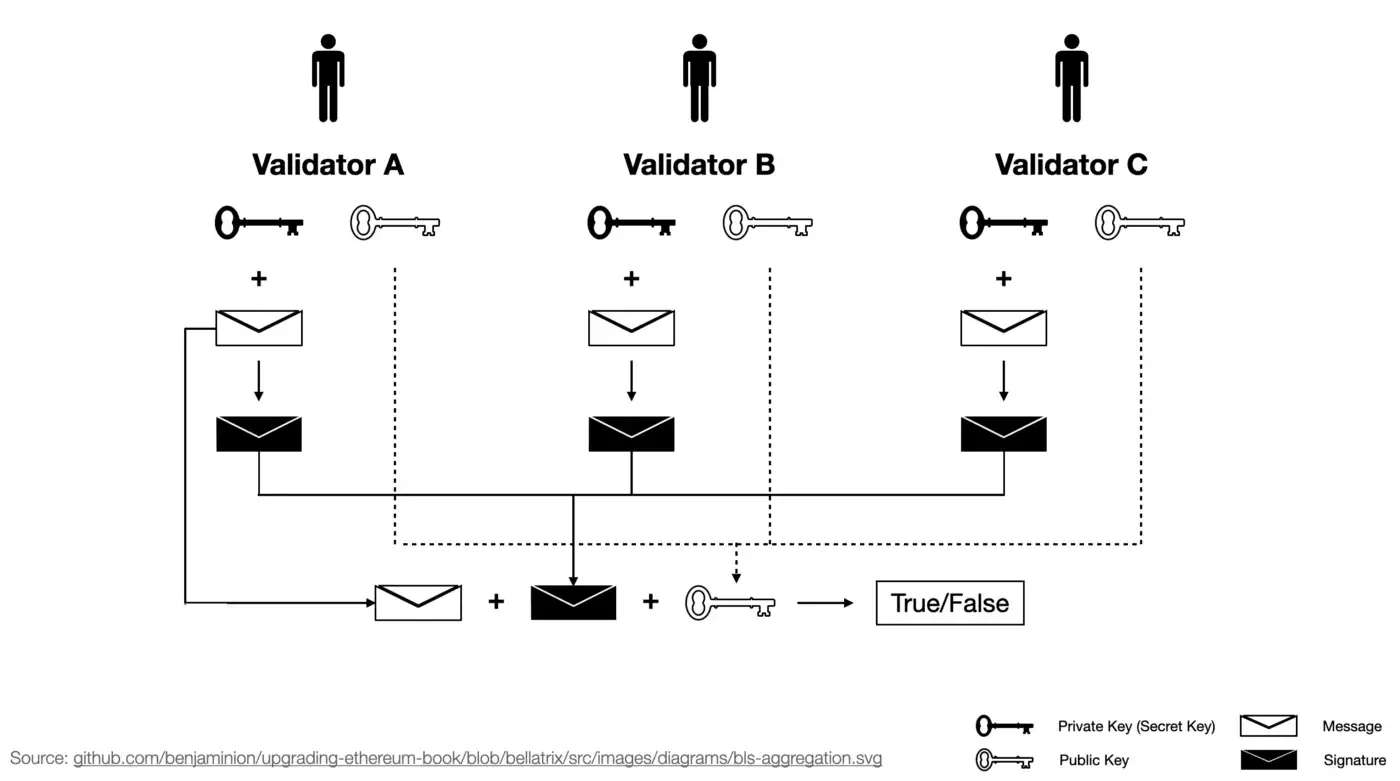
In our previous sections about Light Clients, we know that our most common scenarios are Mobile, Browser, and On-chain. In these scenarios, verifying computations, including aggregating public keys and verifying BLS signature (elliptic curve additions with pairing check), is expensive. Luckily, verifying ZKP, or specifically, zkPoS Attestation is cheap.

Verifying BLS signatures with the BLS12–381 curve is one of the critical components of zkPoS Attestation.

The computing power needed for such expensive verification can be outsourced to zkPoS Attestation prover. Once the proof is generated, there’s no need for other computations.

Then, again, clients just need to verify a ZKP. That simple.

c) More on BLS12–381

A trivial but fun fact about BLS signatures and BLS12–381 is that BLS of “BLS signatures” are Boneh, Lynn, and Shacham, while BLS of “BLS12–381” are Barreto, Lynn, and Scott.

12 in BLS12–381 is the embedding degree of the curve.

381 in BLS12–381 is the number of bits needed to represent coordinates on the curve.

The curve of BLS12–381 is actually two curves: G1 and G2. Other than diving deeper into the Math part of these curves, some engineering decisions on BLS signature are:

G1 is faster and requires less memory than G2 due to a smaller field for calculation.
Zcash chose to use G1 for signatures and G2 for public keys.
Ethereum PoS chose to use G1 for public keys and G2 for signatures. The reason is that aggregation of public keys happens more often, and public keys are stored in states requiring small representation.

The elliptic curve pairing between the two curves is called a bilinear map. The essence is that we map G1 X G2 → Gt. You can learn more in Vitalik’s post.

In simpler words, pairing is a kind of fancy multiplication we need to evaluate BLS signatures. The pairing is what we need for our verification part of BLS signatures of zkPoS Attestation.

4. zkPoS: Halo2 Pairing for BLS

a) Existing Implementations

There are many open-source implementations of pairing on BLS12–381. They are the essential components for implementing verification of BLS signature:

For Ethereum PoS Client: blst by supranational
For Learning: noble-bls12–381 by Paul Miller

Also, some implementation with ZK languages:

For Circom: circom-pairing by 0xPARC (part1 post, part2 post)

b) Hyper Oracle’s Halo2 Pairing

To recap, we need implementation with ZK languages because we will prove PoS with our zkPoS Attestation. BLS signature verification is an essential part of zkPoS Attestation, and pairing on BLS12–381 is the basis for BLS signature verification.

If you read our last post on zkWASM, you may think, why don’t we just use existing implementations? Here’s our thought process:

Reusing Implementations in Rust/C/…: Out-of-the-box solution, but performance may not be optimal directly running them in zkWASM without optimization.
Reusing Implementations in circom (circom-pairing): Also out-of-the-box and audited. Some comparisons will be covered in the next section.

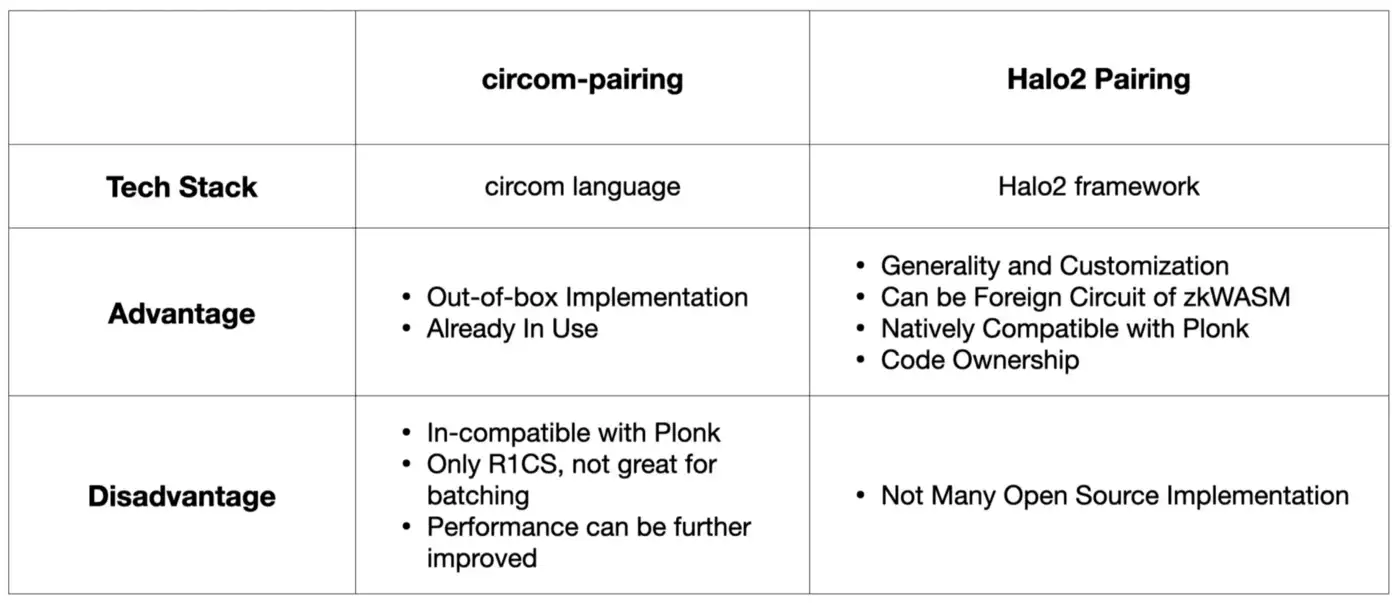
c) Comparison between Halo2 Pairing and circom-pairing

circom-pairing provides a great PoC implementation of pairings for BLS12–381 curve in circom. And it is used for BLS signature verification in Succinct Labs’ Proof of Consensus trustless bridge.

And the reason we don’t use circom-pairing are:

Product-wise: circom-pairing makes customization and generality hard. zkIndexing, and zkAutomation are based on user-defined zkGraph (defines how blockchain data will be extracted, and processed into Hyper Oracle Node), and any logic in zkGraph’s syntax must be supported. This one is closely related to tech-stack-wise reasoning.
Tech-stack-wise: circom-pairing is not natively compatible with Plonkish constraint system of zkWASM and other circuits. circom-pairing in circom compiles to R1CS, and it’s hard to combine with our Plonkish constraint system (without tooling like VampIR that adds more complexity to our system). Also R1CS is not perfect for proof batching (of course possible).
Performance-wise: On proof generation speed, our Halo2 Pairing implementation is much faster than circom-pairing. On gas fee cost, our Halo2 Pairing circuits can be easily integrated with zkWASM circuits (Halo2 Pairing is Plonkish, while circom-pairing is R1CS), so Halo2 Pairing’s gas fee will be much lower.

In simpler words, if we have to use circom-pairing for BLS signature verification, some short-comings for us mainly are:

Incompatible with our existing zk circuits, including zkWASM.
Negative to products’ full generality and customization ability on zkGraph
Or adds unnecessary complexity to our system if we integrate it anyways
And performance may not be optimal

The differences illustrated are:

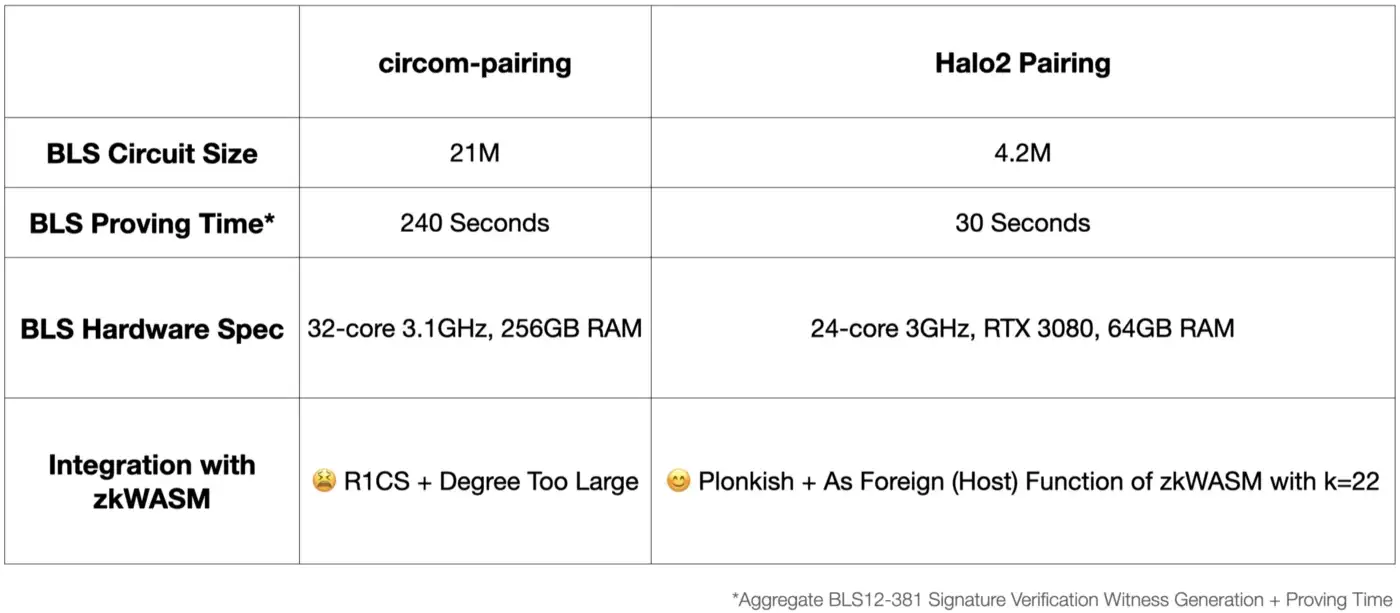
Our final stack is that zkWASM for customized logic (for zkGraph), and Halo2 Pairing as foreign circuit (for BLS with BLS12–381). It satisfies both generality (for user-defined zkGraph) and performance (for the entire zk system).

We are thrilled that we have our own implementation of Halo2 Pairing Library (probably the first open-source implementation out there), ready to power zkPoS Attestation. It is open-sourced, and you can check it here. Below is some more technical details and benchmarks.

5. zkPoS: Recursive Proof

a) ZK Recursion

Another critical point of zkPoS is recursive proof.

Recursive proof is essentially proofs of proofs (verifying proof A when proving B), which our Halo2 Pairing can also potentially play a part in because BLS12–381 is the “zero-knowledge proof curve.”

In general, recursive proof’s main advantage is:

Compression (aka Succinctness):
“Rollup” more knowledge into one outputted single proof.
Eg. Verification(Proof N+1th that proves 0th-Nth’s correctness) < Verification(Proofs 0th-Nth)

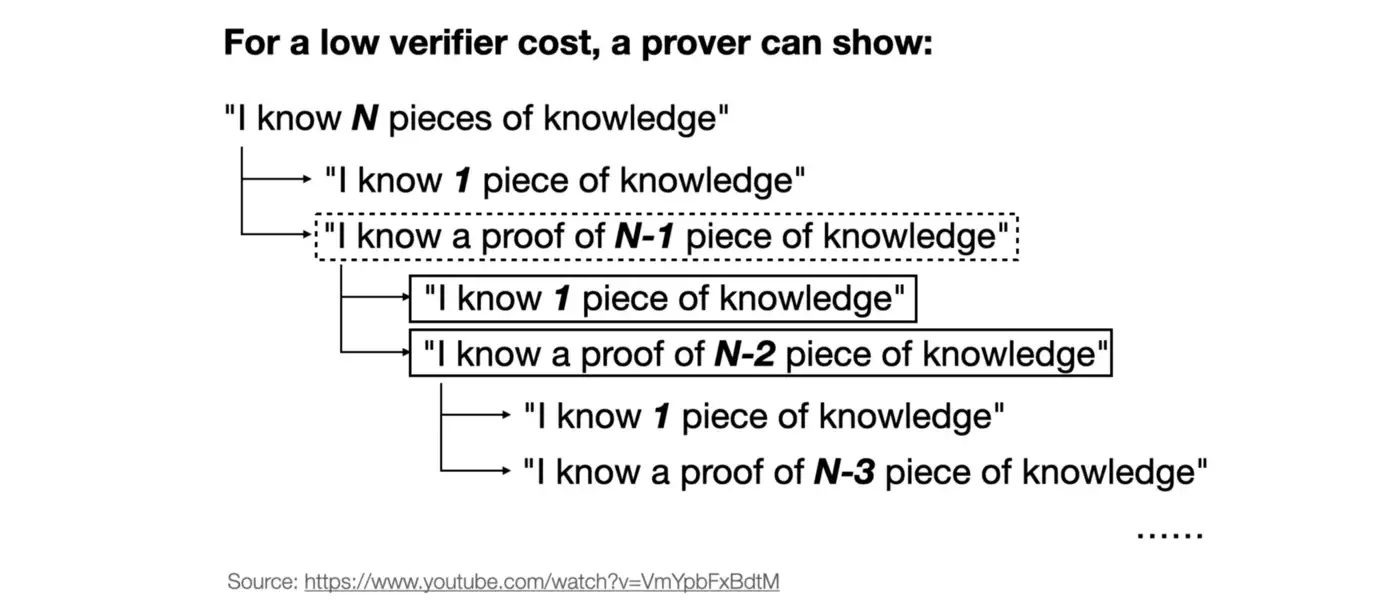
b) Why Recursive Proof for zkPoS?

When dealing with a chain of blocks’ consensus, the need for recursive proof amplifies.

I. Recursive Proof for PoW and PoS

For a network with PoW consensus: Starting from the highest block, we will recursively check its previous hash, nonce, and difficulty until we reach the start block we defined. We will demonstrate the algorithm with formulas in the next section.

For a network like Ethereum with PoS consensus: The case will be more complicated. We need to check every block’s consensus based on the previous block’s validator set and the votes until it’s traced back to a historical block with no dispute (like the genesis block of the Ethereum PoS beacon chain).

II. Effect of Recursive Proof for PoW

The following figure illustrates the effect of recursive proofs for consensus attestations in compressing more information into a single proof, taking PoW as an example.

III. With or Without Recursive Proof

Without recursive proof, we will eventually output O(block height) size proofs to be verified, namely, the public inputs of every block attestation and the proofs for every block.

With recursive proof, except for the public inputs of the initial and the final state, we will have an O(1) for proof for any number of blocks, namely, the first and the final public inputs, together with the recursive proofs pkr. It is a natural question that where have all the intermediate public inputs gone. The answer is that they have become existential quantifiers of the ZK argument and hence canceled out. In simpler words, more knowledge are compressed into the proof by recursive proof.

IV. Effect of Recursive Proof in Hyper Oracle

Remember, we are dealing with “light clients” (browsers) with more computation and memory limitations, even though each proof can be verified in constant time (say, 1 or 2 seconds). If the number of blocks and proofs adds up, the verification time will be very long.

In Hyper Oracle’s zkAutomation, there may be cases of cross-many-block automation that need to be triggered in scenarios like arbitrage strategy or risk management bots. Then a recursive proof for verifying PoS consensus is a must for realizing such an application.

c) Hyper Oracle’s Recursive Proof

This section has been simplified for ease of presentation and understanding and does not represent an exact implementation in practice.

In theory, for applying recursive proof for sequentially two chained blocks, the attestation for PoW‘s case (PoS’s case is too complicated to be written in one formula) will be like this illustration:

After changing the intermediate public variables (namely, h_1, pk_2, and preHash_2) into witnesses, the two proofs can be merged into one proof, as shown below:

We can observe that the public inputs are only h_2, pk_1, and preHash_1. When there are more than two blocks, say, n blocks, we can apply the same technique for n-1 times and fetch a single proof for all the n blocks while preserving only the public inputs of the first pk_1 and preHash_1, along with the final block hash h_n.

A similar algorithm to this PoW example for recursive proof will be applied to keep Hyper Oracle’s zkPoS Attestation succinct and constant with arbitrary block numbers. Note that the customization logic for zkGraph is not included in this recursive proof in the current stage.

6. Path to End-to-end Trustless

Our upcoming yellow paper will provide more specifications and implementation details of Hyper Oracle’s zkPoS Attestation.

To wrap up, zkPoS is based on our unique tech stack of:

zkWASM for providing 100% customization for user-defined zkGraph
Foreign circuits, including Halo2 Pairing
Recursive Proof

Hyper Oracle is excited about realizing end-to-end trustless indexing and automation meta apps with zkPoS and making the next generation of applications truly decentralized with our zkMiddleware.