Initialement publié en anglais par StarkWare le 9 janvier, 2020

Et le rôle symétriques des STARKs
[Cet article a été initialement publié dans Nakamoto. D’après une conférence donnée par Eli Ben-Sasson à San Francisco en novembre 2019]
1. Introduction
Pendant 3,5 milliards d’années, la vie sur Terre a consisté en une soupe primordiale de créatures unicellulaires. Puis, en un clin d’œil géologique, lors de ce qu’on appelle l’explosion Cambrian, presque tous les phyla que nous connaissons aujourd’hui ont émergé.
Par analogie, nous vivons actuellement une explosion cambrienne dans le domaine des preuves cryptographiques d’intégrité computationnelle (CI). Alors qu’il y a quelques années, il y avait environ 1 à 3 nouveaux systèmes par an, le taux a tellement augmenté qu’aujourd’hui nous voyons la même quantité chaque mois, sinon chaque semaine. En 2019, nous avons découvert de nouvelles constructions comme Libra, Sonic, SuperSonic, PLONK, SLONK, Halo, Marlin, Fractal, Spartan, Succinct Aurora, et des implémentations comme OpenZKP, Hodor et GenSTARK. Oh, et alors que l’encre sèche sur ce post, RedShift et AirAssembly arrivent.
Comment donner un sens à toute cette merveilleuse innovation ? L’objet de cet article est d’identifier les dénominateurs communs de tous les systèmes CI implémentés dans le code et d’examiner quelques facteurs de différenciation. La description sera brève et intentionnellement imprécise d’un point de vue mathématique. Un autre objectif majeur de cet article est d’expliquer pourquoi StarkWare place toutes ses atouts en termes de science, d’ingénierie et de produits sur une sous-famille spécifique CI-verse, désormais appelée STARKs symétriques.
Ancêtres communs
Les systèmes de preuves CI peuvent aider à résoudre deux problèmes fondamentaux qui affligent les blockchains décentralisées (et d’autres systèmes) : la confidentialité et la scalabilité. Zero Knowledge Proofs (ZKPs¹) assurent la confidentialité en protégeant certaines entrées d’un calcul sans compromettre l’intégrité, et succinctement les systèmes CI vérifiables offrent la scalabilité en comprimant de façon exponentielle la quantité de calcul nécessaire pour vérifier l’intégrité d’un grand lot de transactions.
Tous les systèmes CI qui ont été réalisés en code ont deux points communs : tous utilisent l’arithmétique et tous appliquent la « conformité à faible degré » (LDC) par des moyens cryptographiques². L’arithmétique est la réduction des déclarations de calcul faites par un prouveur, comme :
« Je connais les clés qui me permettent de passer une transaction Zcash blindée »
à des déclarations algébriques impliquant un ensemble de polynômes à degrés limités, comme :
«Je connais quatre polynômes A(X), B(X), C(X), D(X), de degré inférieur à 1000 chacun, de sorte que cette égalité tienne : A(X) *B²(X) -C(X) = (X¹⁰⁰⁰-1) *D(X) »
La conformité de faible degré implique l’utilisation de la cryptographie pour s’assurer que le prouver sélectionne effectivement les polynômes de faible degré et évalue ces polynômes sur des points choisis au hasard à la demande du vérifieur. Dans l’exemple ci-dessus (dont nous continuerons à nous référer dans ce post), une bonne solution LDC nous assure que lorsque le testeur est interrogé sur x₀, il répondra avec les valeurs a₀, b₀, c₀, d₀ qui sont les valeurs correctes de A, B, C et D sur l’entrée x₀. La partie délicate est qu’un prouver peut choisir A,B,C et D après avoir vu la requête x₀, ou peut décider de répondre avec a₀, b₀, c₀, d₀ arbitraires qui apaisent le vérifieur et ne correspondent à aucune évaluation des polynômes de faible degré présélectionnés. Donc, toute cette cryptographie sert à prévenir de tels vecteurs d’attaque. (La solution triviale qui oblige le prouver à envoyer les A, B, C et D complets n’offre ni la scalabilité, ni confidentialité.)
En gardant cela à l’esprit, le CI-verse peut être cartographié selon :
- les primitives cryptographiques utilisées pour imposer LDC
- les solutions LDC particulières construites avec ces primitives
- le type d’arithmétique permis par ces choix.
2. Dimensions de la comparaison
I. Hypothèses cryptographiques
À partir de 30 000 pieds, le plus grand facteur de distinction théorique entre les différents systèmes de CI est de savoir si leur sécurité nécessite des primitives symétriques ou asymétriques (voir Figure 1). Les primitives symétriques typiques sont SHA2, Keccak (SHA3) ou Blake, et nous supposons qu’il s’agit de fonctions de hachage résistant aux collisions (CRH), pseudorandom et se comportent comme un oracle aléatoire. Les hypothèses asymétriques comprennent des choses comme la dureté de résoudre le problème de logarithme discret modulo un nombre premier, un module RSA, ou dans un groupe de courbe elliptique, la solidité de calculer la taille du groupe multiplicatif d’un cycle RSA, et des variantes plus exotiques de tels problèmes, comme l’hypothèse de « connaissance de l’exposant », l’hypothèse de « racine adaptative.» etc.

Ce fossé de symétrie/asymétrie entre les systèmes CI a de nombreuses conséquences, notamment :
A. Efficacité de calcul
La sécurité des primitives asymétriques implémentées aujourd’hui dans le code⁴ nécessite d’arithmétiser et de résoudre les problèmes LDC sur de grands domaines algébriques : de grands domaines et de grandes courbes elliptiques au-dessus desquels chaque élément de domaine/groupe a des centaines de bits, ou des anneaux entiers dont chaque élément a des milliers de bits. En revanche, les constructions basées uniquement sur des hypothèses symétriques arithmétisent et effectuent des LDC sur n’importe quel domaine algébrique (anneau ou champ fini) qui contient des sous-groupes lisses⁵, y compris de très petits domaine binaires et de 2 domaines primaires lisses (64 bits ou moins), où les opérations arithmétiques sont rapides.
À retenir : les systèmes de CI symétriques peuvent arithmétiser sur n’importe quel domaine, ce qui permet une plus grande efficacité.
B. Sécurité post-quantique
Toutes les primitives asymétriques actuellement utilisées dans le CI-verse seront brisées efficacement par un ordinateur quantique avec un état suffisamment grand (mesuré en qubits), si et quand un tel ordinateur apparaît. Les primitives symétriques, par contre, sont vraisemblablement sécurisées post-quantique (peut-être avec des données d’entrée plus grandes et des états par bit de sécurité).
À retenir : Seuls les systèmes symétriques sont certainement sécurisés post-quantique.

C. Protéger l’avenir
La théorie de l’effet Lindy dit que « l’espérance de vie future de certaines choses non périssables comme une technologie ou une idée est proportionnelle à leur âge actuel. » Dans le domaine de la cryptographie, cela peut se traduire par l’affirmation que les systèmes qui reposent sur des primitifs plus anciens et éprouvés au combat sont plus sûrs et plus à l’épreuve du temps que les postulats plus récents dont les pneus ont été moins touchés (voir la figure 2). De ce point de vue, les nouvelles variantes d’hypothèses asymétriques comme les groupes d’ordre inconnu, le modèle générique de groupe et la connaissance des hypothèses d’exposant sont plus jeunes et ont tiré un panier économique plus léger que les hypothèses plus anciennes comme les hypothèses DLP et RSA plus standard utilisées, p.ex. pour les signatures numériques, le chiffrement basé sur l’identité et l’initialisation SSH. Ces hypothèses sont moins à l’épreuve du temps que les hypothèses symétriques comme l’existence d’un hachage résistant aux collisions, car ces dernières hypothèses (et même certaines fonctions de hachage) constituent la pierre angulaire de la sécurité des ordinateurs, des réseaux, de l’Internet et de l'e-commerce.
De plus, il y a une hiérarchie mathématique stricte entre ces hypothèses. L’hypothèse CRH prévaut dans cette hiérarchie car si cette hypothèse est rompue (c’est-à-dire qu’aucune fonction de hachage cryptographique sûre n’est trouvée), les hypothèses RSA et DLP sont également rompues car elles impliquent l’existence d’un bon CRH ! De même, l’hypothèse DLP prévaut sur la connaissance de l’hypothèse de l’exposant (KoE) parce que si la première hypothèse (DLP) ne tient pas, la seconde hypothèse (KoE) ne tient pas non plus. De même, les hypothèses RSA règnent sur l’hypothèse du groupe d’ordre inconnu (GoUO) parce que si RSA est rompu, alors GoUO se rompt aussi.
Points à retenir : Les nouvelles hypothèses asymétriques constituent une base plus risquée pour l’infrastructure financière.
D. Longueur des arguments
Tous les points ci-dessus favorisent les constructions CI symétriques par rapport aux constructions asymétriques. Mais il y a un domaine où les constructions asymétriques s’en sortent mieux. La complexité de la communication (ou la longueur de l’argument) qui leur est associée est inférieure de 1 à 3 ordres de grandeur (malgré la loi⁶ de Nielsen). Il est connu que le Groth16 SNARK est inférieur à 200 octets pour un niveau de sécurité estimé à 128 bits, alors que toutes les constructions symétriques existantes requièrent des dizaines de kilo-octets pour le même niveau de sécurité. Il convient de noter que toutes les constructions asymétriques ne sont pas aussi succinctes que 200 octets. Les constructions récentes améliorent Groth16 en (i) éliminant la nécessité d’une configuration fiable (transparence) et/ou (ii) en gérant les circuits généraux (Groth16 nécessite une configuration fiable par circuit). Mais ces constructions plus récentes ont des arguments qui sont plus longs, allant d’un demi-kilo-octet (comme c’est le cas de PLONK) à un nombre de kilo-octets à deux chiffres, se rapprochant de la longueur d’argument des constructions symétriques.
À retenir : les systèmes asymétriques spécifiques aux circuits (Groth16) sont les plus courts, plus courts que tous les systèmes asymétriques universels et tous les systèmes symétriques.
Pour réitérer les points à retenir ci-dessus :
- Les systèmes CI symétriques peuvent arithmétiser sur n’importe quel domaine, ce qui permet une plus grande efficacité
- Seuls les systèmes symétriques sont certainement sécurisés post-quantique
- De nouvelles hypothèses asymétriques constituent une base plus risquée pour l’infrastructure financière
- Les systèmes asymétriques spécifiques aux circuits (Groth16) sont les plus courts, plus courts que tous les systèmes asymétriques universels, et tous les systèmes symétriques
II. Low Degree de conformité (LDC) schéma
Il existe deux principaux moyens d’atteindre un Low Degree de conformité: i) les requêtes cachées et ii) les mécanismes d’engagement (voir figure 3). Passons en revue les différences.
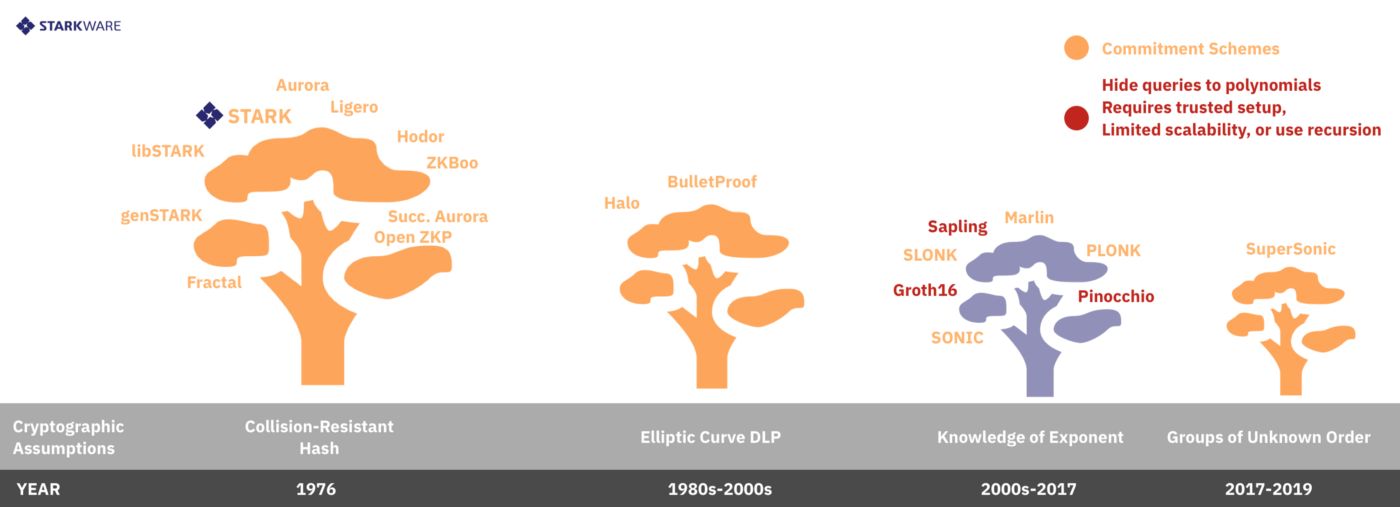
Cacher les requêtes
Cette approche (formalisée ici) est celle utilisée par les SNARK de style Zcash comme Pinocchio, libSNARK, Groth16, et les systèmes construits sur eux comme Sapling de Zcash, Zokrates d’Ethereum, etc. Pour que le testeur réponde correctement, nous utilisons le homomorphic encryption pour masquer, ou chiffrer, x₀ et fournir suffisamment d’informations pour que le prouver puisse évaluer A, B, C et D sur x0 . En fait, ce qui est donné au prouver est une séquence de chiffrement de puissances de x0 (cad, chiffrement de x₀¹ , x₀², … x₀¹⁰⁰⁰) de sorte que le prouver peut évaluer n’importe quel polynôme de degré-1000 mais seulement des polynômes de degré au plus 1000. En gros, le système est sécurisé puisque le prouver ne sait pas ce qu’est x₀, et ce x₀ est sélectionné au hasard (pré-) de sorte que si le prouver tente de tricher, il sera exposé avec une probabilité très élevée. Une phase d’initialisation fiable est nécessaire ici pour échantillonner x₀ et chiffrer la séquence de puissances ci-dessus (et les informations supplémentaires), conduisant à une clé de test qui est au moins aussi grande que le circuit du calcul testé (il y a aussi une clé de vérification qui est beaucoup plus courte). Une fois la configuration terminée et les clés libérées, chaque preuve est un succinct, noninteractive argument of knowledge (ou SNARK, en abrégé). Notez que ce système nécessite une certaine forme d’interaction, sous la forme de la phase d’initialisation, ce qui est inévitable pour des raisons théoriques. Notez également que le système n’est pas transparent, ce qui signifie que l’entropie utilisée pour échantillonner et chiffrer x₀ ne peut pas être simplement des pièces publiques aléatoires, car toute partie connaissant x₀ peut briser le système et prouver des faussetés. Générer un chiffrement de x₀ et de ses pouvoirs sans révéler x₀ est donc un problème de sécurité qui constitue un point de défaillance unique potentiel.
Systèmes d’engagement
Cette approche exige que le prouveur s’engage sur l’ensemble des polynômes de Low Degree (A, B, C et D, dans l’exemple ci-dessus) en envoyant un message d’engagement cryptographiquement conçu au vérifieur. Avec cet engagement en main, le vérifieur échantillonne et interroge le prouveur au sujet d’un x₀ choisi au hasard, et l’étalon répond avec a₀, b₀, c₀, et d₀ ainsi que des informations cryptographiques supplémentaires qui convainquent le vérifieur que les quatre valeurs révélées par le prouveur sont conformes à l’engagement précédent envoyé au vérifieur. Ces systèmes sont naturellement interactifs et beaucoup d’entre eux sont transparents (tous les messages générés par le vérifieur ne sont que des pièces publiques aléatoires). La transparence permet de compresser le protocole en un protocole non-interactif via Fiat-Shamir heuristic (qui traite une fonction pseudorandom comme SHA 2/3 comme un oracle aléatoire qui fournit l’aléatoire « public »), ou d’utiliser d’autres sources publiques d’aléatoire comme les en-têtes de blocs. Le schéma d’engagement transparent le plus répandu est par l’intermédiaire du Merkle trees, et cette méthode est plausiblement sécurisée post-quantique, mais conduit aux grandes longueurs d’arguments observées dans de nombreux systèmes symétriques (en raison de tous les chemins d’authentification qui doivent être révélés et accompagnant chaque réponse de test). C’est la méthode utilisée par la plupart des STARKs comme libSTARK et Aurora succinct, ainsi que par les systèmes de preuve succincts comme ZKBoo, Ligero, Aurora et Fractal (même si ces systèmes ne répondent pas à la définition formelle d’évolutivité d’un STARK). En particulier, les STARKs que nous construisons chez StarkWare (comme StarkDEX Alpha et le StarkExchange que nous allons déployer prochainement) entrent dans cette catégorie. On peut utiliser des primitives asymétriques pour construire des schémas d’engagement, par exemple ceux basés sur la dureté du problème de logarithme discret sur des groupes de courbes elliptiques (c’est l’approche adoptée par BulletProofs et Halo), et les groupes d’hypothèse d’ordre inconnu (comme fait par DARK et SuperSonic). L’utilisation de schémas d’engagement asymétrique présente les avantages et les inconvénients mentionnés précédemment : preuves plus courtes mais temps de calcul plus long, susceptibilité quantique, hypothèses nouvelles (et moins étudiées) et, dans certains cas, perte de transparence.
III. Arithmétique
Le choix des hypothèses cryptographiques et des méthodes LDC influe également sur l’éventail des possibilités d’arithmétique, de trois façons notables (voir la figure 4) :

A. PN (circuits) et NEXP (programmes)
La plupart des systèmes de CI implémentés réduisent les problèmes de calcul à des circuits arithmétiques qui sont ensuite convertis en un ensemble de contraintes (habituellement, contraintes R1CS, examinées ci-dessous). Cette approche permet des optimisations spécifiques au circuit, mais exige que le vérifieur, ou une entité de confiance, effectue un calcul aussi grand que le calcul (circuit) vérifié. Pour les circuits polyvalents comme le circuit Sapling de Zcash, cette arithmétique suffit. Mais les systèmes scalable et transparents (aucune configuration initial fiable) comme libSTARK, Aurora succincte et les systèmes que StarkWare construit, doivent utiliser une représentation succincte du calcul, semblable à un programme informatique général et dont la description est exponentiellement plus petite que le calcul vérifié. Les deux méthodes existantes pour y parvenir – (i) les représentations intermédiaires algébriques (AIR) utilisées par les systèmes libSTARK, genSTARK et StarkWare, et (ii) le R1CS succinct de succinct-Aurora, sont mieux décrites comme des arithmétiques de programmes informatiques généraux (par opposition aux circuits). Ces représentations succinctes sont suffisamment puissantes pour saisir la classe de complexité du temps exponentiel non déterministe (NEXP), qui est exponentiellement plus expressive et puissante que la classe du temps polynomial non déterministe (NP) décrite par les circuits.
B. Taille et type de l’alphabet
Comme indiqué ci-dessus, les hypothèses cryptographiques utilisées dictent aussi dans une large mesure quels domaines algébriques peuvent servir d’alphabet sur lequel nous calculons. Par exemple, si nous utilisons des paires bilinéaires, alors l’alphabet que nous utiliserons pour l’arithmétique est un groupe cyclique de points de courbe elliptiques, et ce groupe doit être de grande taille premier, ce qui signifie que nous devons arithmétiser sur ce champ. Pour prendre un autre exemple, le système SuperSonic (dans une de ses versions) utilise des entiers RSA et dans ce cas l’alphabet sera un grand domaine premier. En revanche, lors de l’utilisation Merkle Tree, la taille de l’alphabet peut être arbitraire, permettant l’arithmétique sur n’importe quel domaine fini. Cela inclut les exemples ci-dessus mais aussi les champs premiers arbitraires, les extensions de petits champs premiers tels que les champs binaires. Le type de champ est important car les champs plus petits conduisent à un temps de test et de vérification plus rapide.
C. R1CS vs. Contraintes polynomiales générales
Les SNARKs de type Zcash utilisent des paires bilinéaires sur des courbes elliptiques pour arithmétiser les contraintes du calcul. Cette utilisation⁷ particulière des paires bilinéaires limite l’arithmétique aux barrières qui sont des systèmes de contrainte de Rank-1 Constraint Systems (R1CS). La simplicité et l’omniprésence du R1CS ont conduit de nombreux autres systèmes à utiliser cette forme d’arithmétique pour les circuits, même si des formes plus générales de contraintes peuvent être utilisées, comme des formes quadratiques arbitraires ou des contraintes de degré supérieur.
3. STARK contre SNARK
C’est une bonne occasion de clarifier les différences entre les STARKs et les SNARKs. Les deux termes ont des définitions mathématiques concrètes, et certaines constructions peuvent être instanciées comme STARKs, SNARKs, ou les deux. Les différents termes mettent l’accent sur les différentes propriétés des systèmes de preuves. Examinons-les plus en détail (voir Figure 5).

STARK
Le S représente ici la scalabilité, ce qui signifie que lorsque la taille du lot n augmente, démontrant les échelles de temps quasi-linéairement en n et, simultanément, vérifiant les échelles de temps de manière poly-logarithmique⁸ en n. Le T de STARK est synonyme de transparence, ce qui signifie que tous les messages du vérifieur sont des pièces publiques aléatoires (aucune configuration fiable). Selon cette définition, s’il y a une configuration initiale, celle-ci doit être succincte (poly-logarithmique) et consister simplement en un échantillonnage aléatoire de random coins.
SNARK
Le S est ici synonyme de Succinctness, ce qui signifie que la vérification est poly-logarithmique en n (sans exiger de temps de test quasi linéaire) et le N signifie non-interactif, ce qui signifie qu’après une phase de prétraitement (qui peut ne pas être transparente), le système de preuve ne permet plus d’interaction. Notez que selon cette définition, une phase de configuration initiale fiable non succincte est autorisée, et, d’une manière générale, le système n’a pas besoin d’être transparent, mais il doit être non interactif (après la finalisation de la phase initiale, ce qui est inévitable).
Si l’on examine le CI-verse (voir la figure 5), on remarque que certains de ses membres sont des STARKs, d’autres des SNARKs, certains sont les deux, tandis que d'autres ne sont ni l'un ni l'autre (p.ex, si la scalabilité de temps de vérification est inférieure à la poly-logarithmique en n). Si vous êtes intéressé par les applications de protection de la vie privée (ZKP), les ZK-SNARK et ZK-STARK et même les systèmes qui n’ont ni la scalabilité d’un STARK ni la (plus faible) concision d’un SNARK pourraient être utiles; Bulletproofs, utilisé par Monero, en est un exemple notable, où le temps de vérification varie linéairement avec la taille du circuit. Quand il s’agit de la maturité du code, les SNARKs ont un avantage car il y a pas mal de bonnes bibliothèques open source sur lesquelles construire. Mais si vous êtes intéressé par les applications de scalabilité (où vous devez construire des lots de plus en plus volumineux), nous vous suggérons d’utiliser des STARKs symétriques, car au moment de la rédaction de cet article, ils ont le temps de test le plus rapide et sont assurés qu’aucune partie du processus de vérification (ou de la configuration initiale du système) ne nécessite plus que du temps de traitement poly-logarithmique. Et si vous voulez construire des systèmes qui ont des hypothèses de confiance minimales, alors, encore une fois, vous voulez utiliser un STARK symétrique parce que le seul ingrédient nécessaire est un peu de CRH et une source d’aléatoire public.
4. Résumé

Nous avons la chance de vivre la merveilleuse explosion Cambrian dans l’univers de l’Intégrité Computationnelle des systèmes de preuve, et tous les paris sont que la prolifération des systèmes et des innovations va se poursuivre, à un rythme croissant. De plus, cette tentative de décrire le CI-verse en expansion et en mutation vieillira probablement mal à mesure que de nouvelles idées et constructions apparaîtront demain. Cela dit, si l’on examine aujourd’hui l’espace CI, la plus grande ligne de démarcation se situe entre (i) les systèmes qui nécessitent des hypothèses cryptographiques asymétriques – qui conduisent à des preuves plus courtes mais plus coûteuses à prouver, qui ont des hypothèses plus récentes qui sont sensibles aux quantiques et dont beaucoup ne sont pas transparentes, et (ii) les systèmes qui reposent uniquement sur des axes symétriques Impressions, ce qui les rend efficaces sur le plan informatique, transparentes, plausiblement sécurisées post-quantique et les plus à l’épreuve du temps (selon la métrique de Lindy Effect).
L’argument sur le système d’arguments à utiliser est loin d’être terminé. Mais chez StarkWare, nous disons : Pour des arguments courts, utilisez Groth16/PLONK SNARKs. Pour tout le reste, il y a des STARKs symétriques.
Eli Ben-Sasson, StarkWare
Nous remercions tout particulièrement Justin Drake d’avoir commenté cette version préliminaire.
— — — — — — — — — — — — — —
¹ Le terme ZKP est souvent utilisé à mauvais escient pour désigner tous les systèmes Sulf-Custody, même ceux qui ne sont pas officiellement des ZKP. Pour éviter cette confusion, nous utilisons les termes vaguement définis de «preuves cryptographiques» et «preuves d’intégrité computationnelle (CI) .»
² Vous pouvez lire sur l’arithmétique STARK et la conformité à faible degré ici:
- Arithmétique : blogs [1, 2], slides et vidéoconférences.
- Low Degreeneess : article du blog (pour les STARKs)
³ L’utilisation des polynômes univariés peut être généralisée à grande échelle, par exemple aux polynômes multivariés et aux codes de géométrie algébrique, mais pour simplifier nous nous en tenons au cas le plus simple, univarié.
⁴ Nous excluons expressément les constructions en maille de notre discussion, car elles ne sont pas encore déployées en code. De telles constructions sont asymétriques et, de façon plausible, sécurisées post-quantique, et utilisent généralement de petits champs (primaires).
⁵ Un champ est lisse-k s’il contient un sous-groupe (multiplicatif ou additif) de taille dont tous les diviseurs primaires sont au plus k. Par exemple, tous les champs binaires sont 2 lisses, et donc les champs de taille q tel q-1 est divisible par une grande puissance de 2.
⁶ La loi de Nielsen sur la bande passante Internet stipule que la bande passante des utilisateurs augmente de 50% par an. Cette loi s’applique aux données de 1983 à 2019.
⁷ D’autres systèmes (comme PLONK) n’utilisent les couplages que pour obtenir un schéma d’engagement (polynôme) et non pour l’arithmétique. Dans de tels cas, l’arithmétique peut entraîner des contraintes de faible degré.
⁸ Formellement, «quasi-linéaire en n» signifie O(n logᴼ⁽¹⁾ n) et «poly-logarithmique en n» signifie logᴼ⁽¹⁾ n.
Traduction faite par @cleminso